| MONOGRÁFICO: Matemáticas y las TIC - GEOGEBRA |
 |
 |
 |
| EQUIPAMIENTO TECNOLÓGICO - Didáctica de la tecnología | |||||||||||||||
| Elvira Mifsud-k idatzia | |||||||||||||||
| Astelehena, 2010(e)ko ekaina(r)en 28-(e)an 00:00etan | |||||||||||||||
JPAGE_CURRENT_OF_TOTAL
GEOGEBRAIntroducciónEn este artículo vamos a estudiar una aplicación que permite trabajar con geometría dinámica, álgebra y cálculo utilizando el ordenador. Se llama Geogebra y su objetivo es ser una alternativa para la docencia en geometría, álgebra, etc, de forma integrada, dinámica y atractiva para el alumnado. Es una aplicación de software libre, creada por Markus Hohenwarter desde el departamento de Didáctica de la Matemática de la Universidad de Salzburgo y que ha recibido varios premios o reconocimientos, entre ellos el European Academic Software Award (2002), el International Free Software Award, categoría de educación (2005) y el Distinguished Development Award otorgado por la Association for Educational Communications and Technology de Orlando (2008), entre otros. La página web del proyecto es http://www.geogebra.org. Geogebra: característicasLa última versión disponible es la 3.2. Se trata de software libre con licencia GPL para cualquier uso no comercial (http://www.geogebra.org/download/license.txt). Relacionada con Geogebra su uso y difusión es de interés la siguiente wiki en español http://www.geogebra.org/en/wiki/index.php/Spanish. Existen versiones para Windows, Mac OS y GNU/Linux (32bit/64bit). Nosotros vamos a utilizar la versión para GNU/Linux 32 bit. Los ejercicios construidos (construcciones utilizando la terminología de Geogebra) son portables, además de permitir a partir de ellas generar páginas web dinámicas. Geogebra ejecuta un archivo Java (geogebra.jar) y almacena cada uno de los ejercicios o construcciones en un archivo XML con de extensión ggb. Podemos decir que Geogebra está formada por un conjunto de objetos básicos, un conjunto de acciones elementales a realizar sobre estos objetos, un lenguaje de programación que utiliza una sintaxis específica y una interfaz gráfica que permite trabajar, operar y relacionar estos objetos. Desde esta interfaz dinámica e interactiva, los usuarios pueden diseñar, programar y ejecutar acciones y obtener resultados matemáticos del tipo gráficos (interactivos), cálculos, simulaciones, etc. Las principales características de Geogebra son:
Instalación y configuraciónInstalación Existe un paquete .deb de Geogebra para ser instalado en Ubuntu 9.10 Jaunty. Los pasos a seguir para la instalación son los siguientes:
Pero la versión que proporciona este paquete es la 3.0. Si preferimos trabajar con la última 3.2 deberemos hacerlo con el archivo GeoGebra-Linux-Portable-3.2-42-0.tar.gz que descargamos desde http://www.geogebra.org/cms/es/installers. 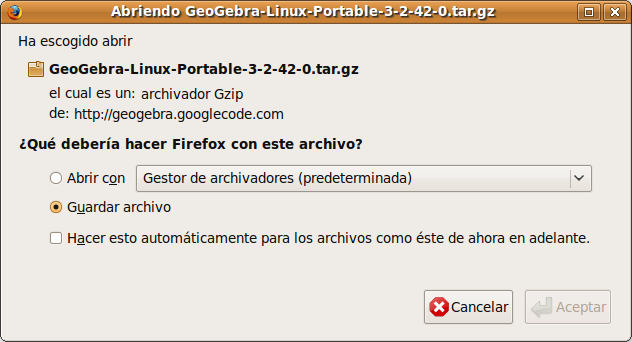 En este caso los pasos a seguir son los siguientes:
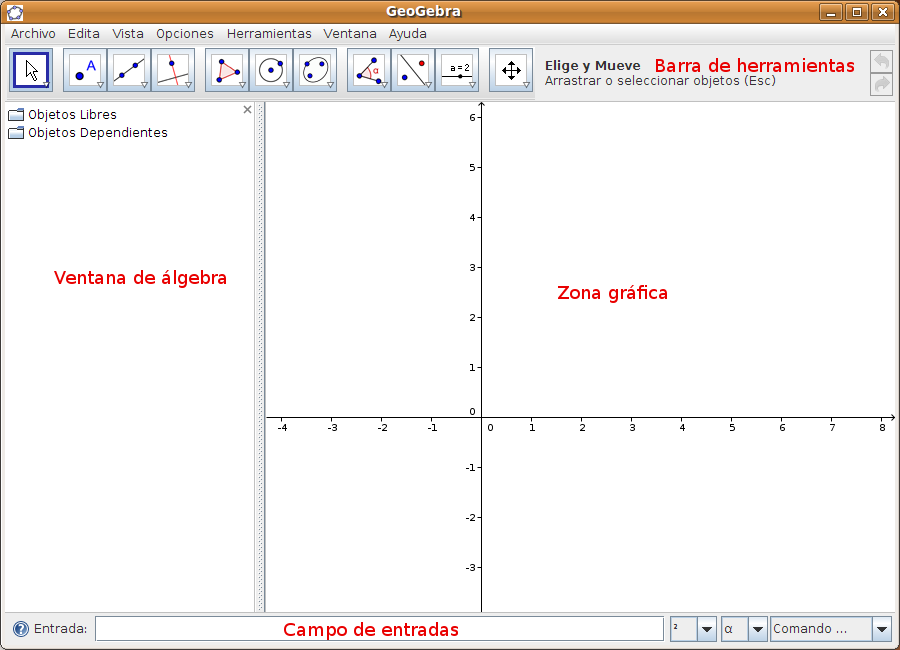
Las zonas de trabajo disponibles son:
Existe aún una zona llamada de Hoja de cálculo. En esta zona o vista cada celda se identifica por su fila y columna. Por ejemplo A1 es la celda situada en la fila 1 columna A. Este nombre puede utilizarse en expresiones u órdenes haciendo referencia a su contenido. En las celdas se pueden incluir números, coordenadas de puntos, funciones, etc y si tienen correspondencia gráfica se verá en la zona gráfica. Tipos de objetos En la zona de álgebra vemos que hay dos tipos de objetos matemáticos:
Tipos de construcciones
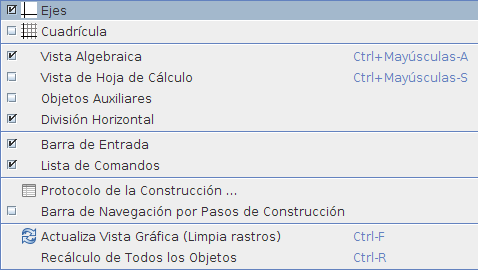
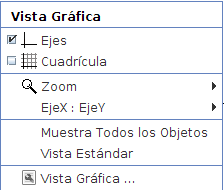
Personalización de la interfaz de usuario Desde el menú Vista se puede mostrar u ocultar las vistas y otros elementos de la interfaz gráfica:
En el menú Vista podemos activar la Barra de Navegación por Pasos de Construcción que incluye al pie de la vista gráfica un botón de reproducción de los diferentes pasos que realizado para la construcción.
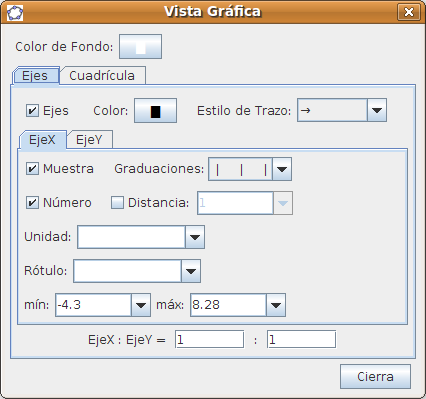
En Opciones > Vista Gráfica podemos establecer los parámetros que determinan los ejes X e Y y su color así como las características de la cuadrícula.
El menú contextual en la vista gráfica incluye una herramienta de zoom de aproximación y alejamiento:
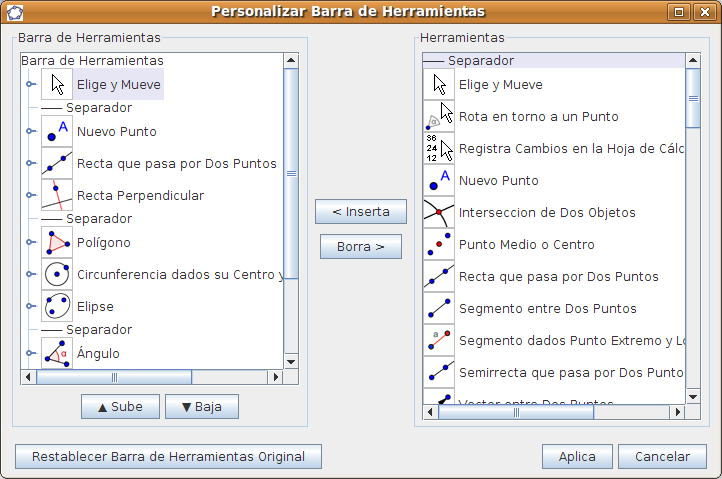
La Barra de Herramientas se puede personalizar desde el menú Herramientas > Personalizar Barra de Herramientas:
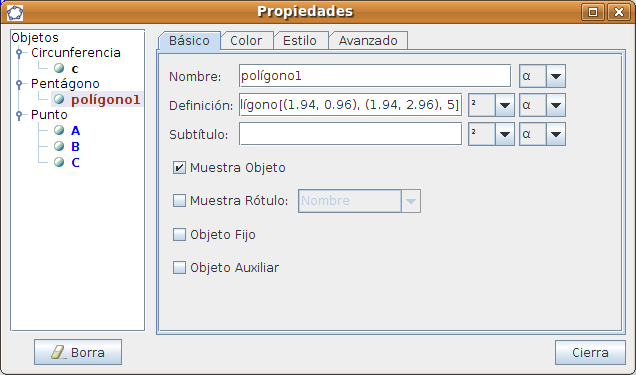
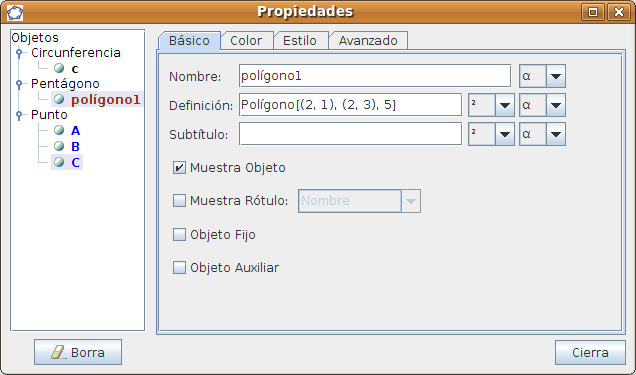
Propiedades de los objetos El usuario puede conocer y actuar sobre las propiedades de los objetos que va creando. Para ello se puede situar tanto en la zona gráfica como en la de álgebra y pulsando el botón derecho seleccionar Propiedades:
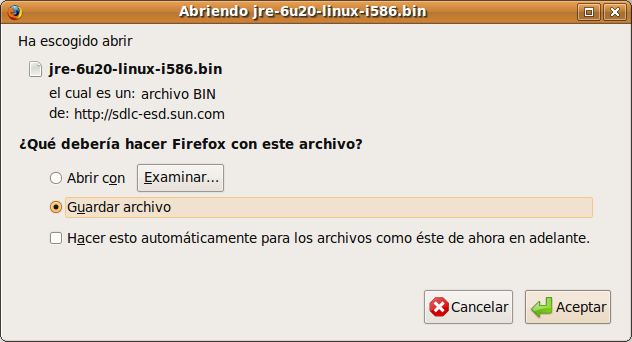
En este caso vemos las propiedades de un polígono: nombre, datos de su construcción y podemos establecer su estilo de trazo, color, etc. Instalación de javaGeoGebra requiere tener instalado en el ordenador Java. Podemos comprobar si nuestro ordenador ya dispone de Java accediendo a la página http://www.java.com y ejecutando el test de comprobación. Desde esta página también se puede descargar la versión para Ubuntu junto con el manual de instrucciones para su correcta instalación (http://java.com/es/download/linux_manual.jsp).
Nos descargamos la versión para Linux (archivo autoextraible) jre-6u20-linux-i586.bin. Para instalar:
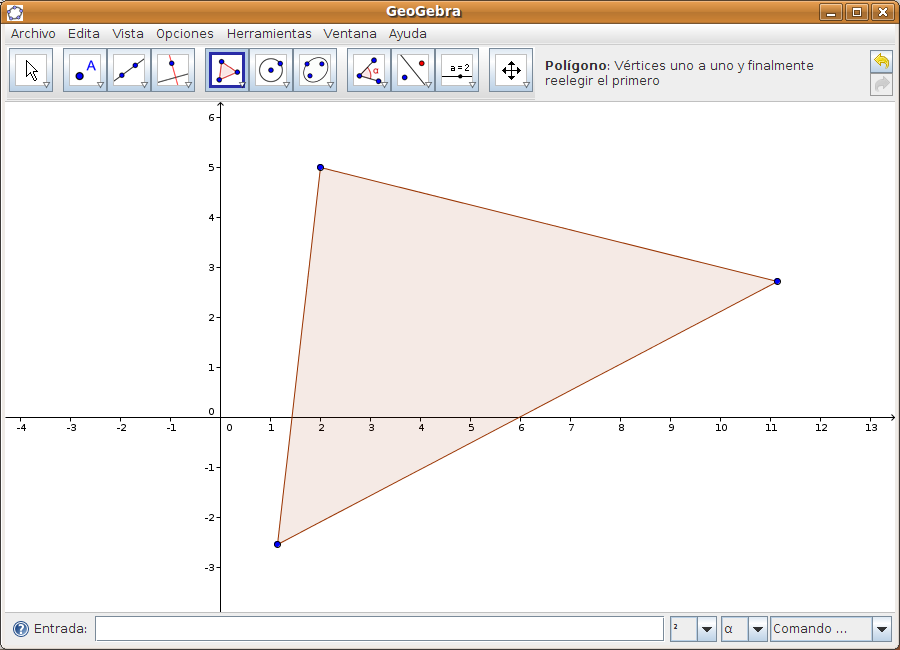
Utilización de Geogebra: casos prácticosPartimos del supuesto de que la práctica es la mejor forma de evaluar la herramienta. Por ello, vamos a estudiar el funcionamiento de Geogebra mediante la realización de varios casos prácticos, todos ellos muy sencillos. Caso 1Vamos a dibujar la circunferencia inscrita en un triángulo cualquiera. Paso 1 Cerramos la ventana de Álgebra. En la zona gráfica seleccionamos la función Polígo
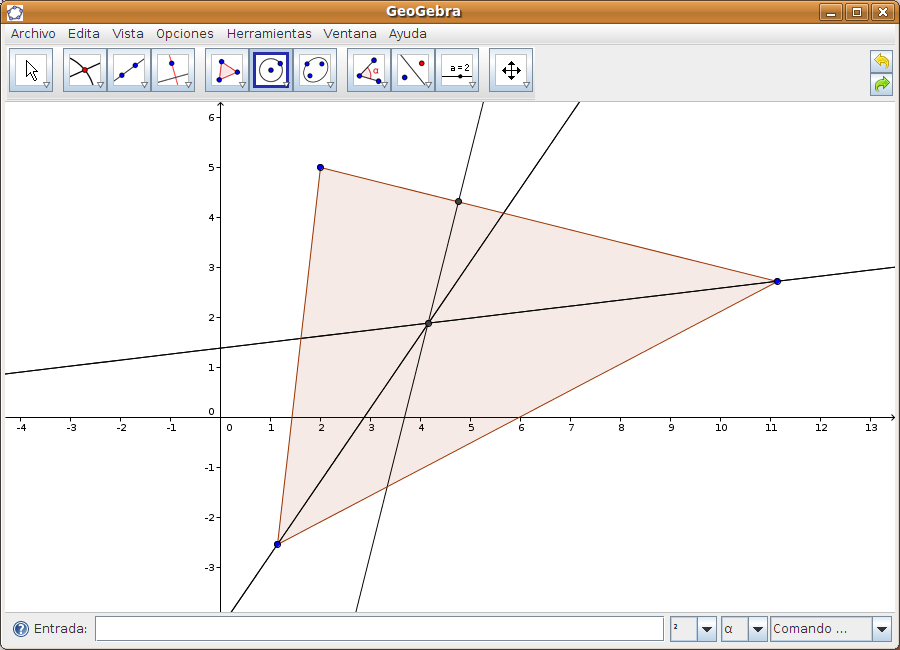
Paso 2 Dibujamos las bisectrices de dos de los tres ángulos S Seleccionamos el punto de intersección de ambas bisectrices y calculamos la perpendicular desde este punto de intersección hasta el lado opuesto.
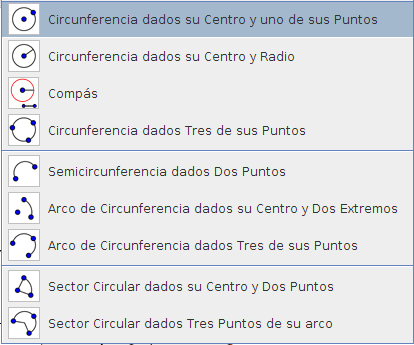
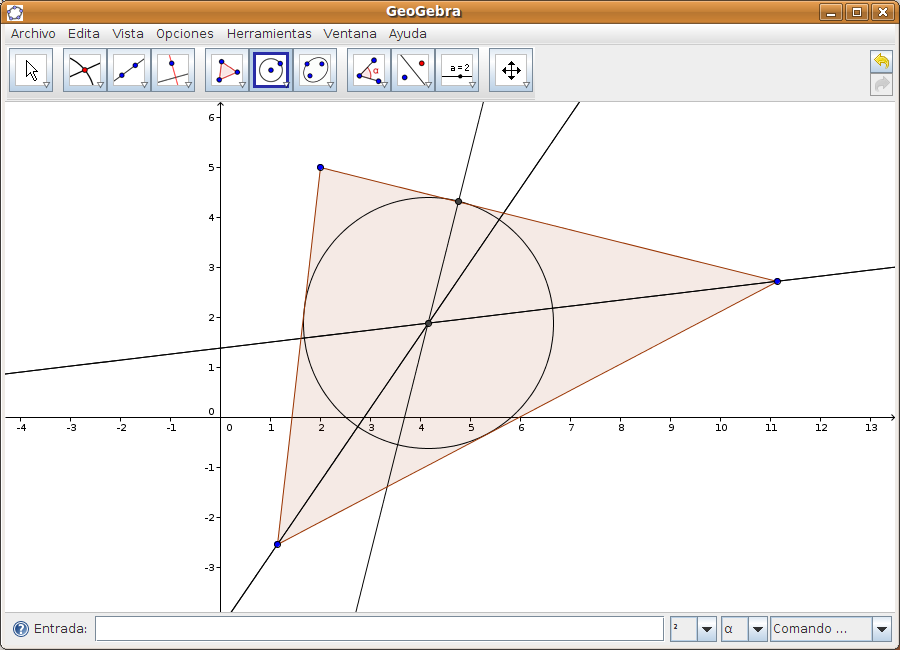
Paso 3 Dibujo de la circunferencia inscrita Seleccionamos la opción marcada en:
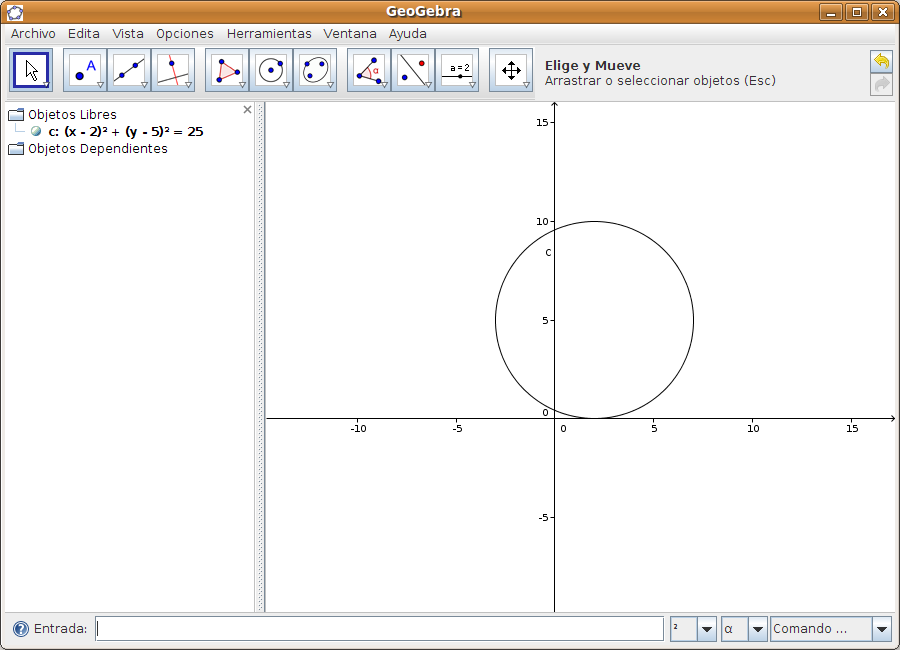
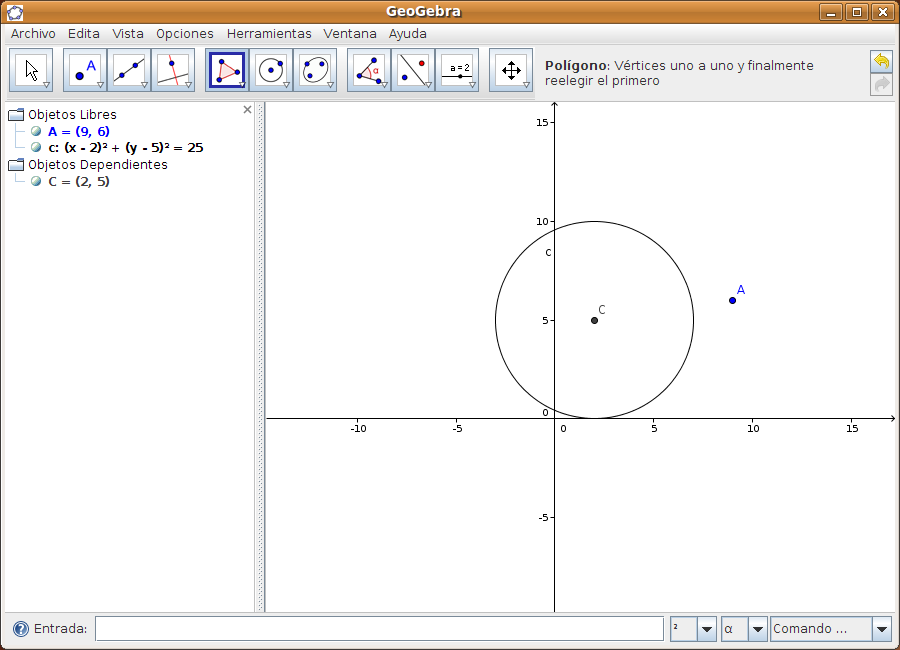
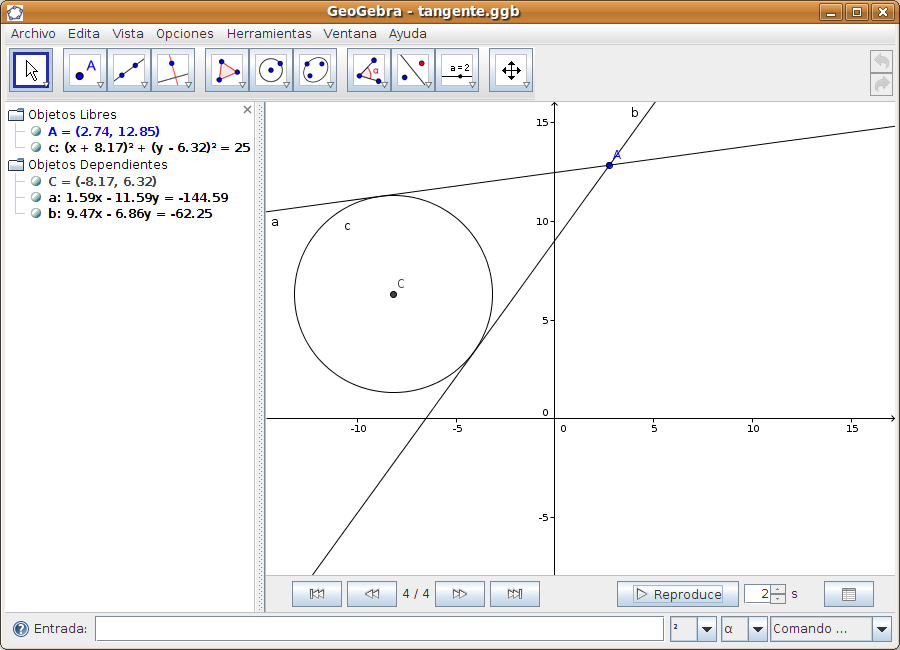
Guardar la construcción desde Archivo > Guardar como. Caso 2Tenemos la ecuación de la circunferencia c (x - 2)² + (y - 5)² = 25 y queremos representar tanto la circunferencia como sus tangentes que pasan por el punto A de coordenadas (9, 6). Paso 1 Introducir la ecuación de la circunferencia (x - 3)² + (y - 2)² = 25 en la zona de entradas y pulsar INTRO.
Paso 2
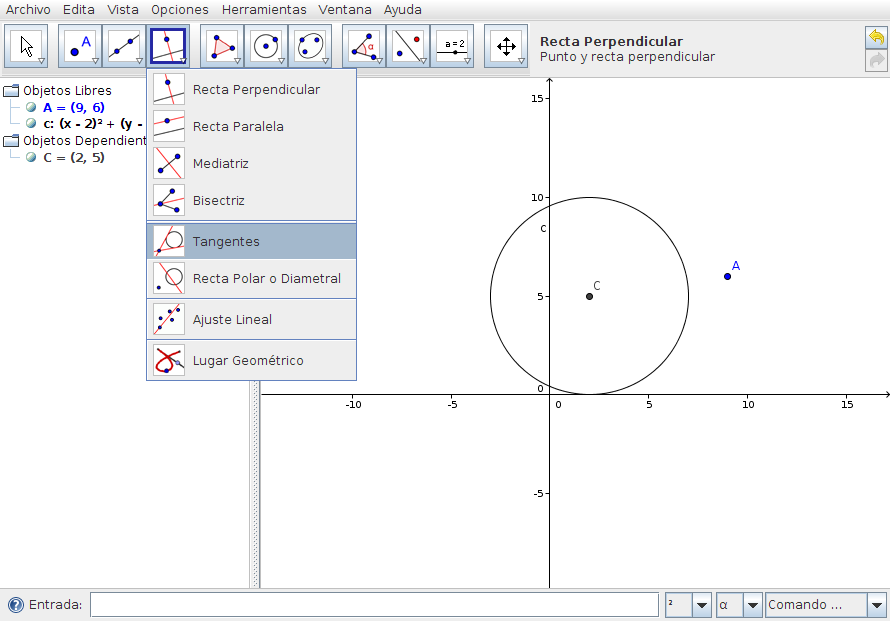
Paso3 Ir a la Barra de Herramientas y desplegar el cuarto icono. Seleccionar el modo Tangentes y hacer clic sobre el punto A y sobre la circunferencia c.
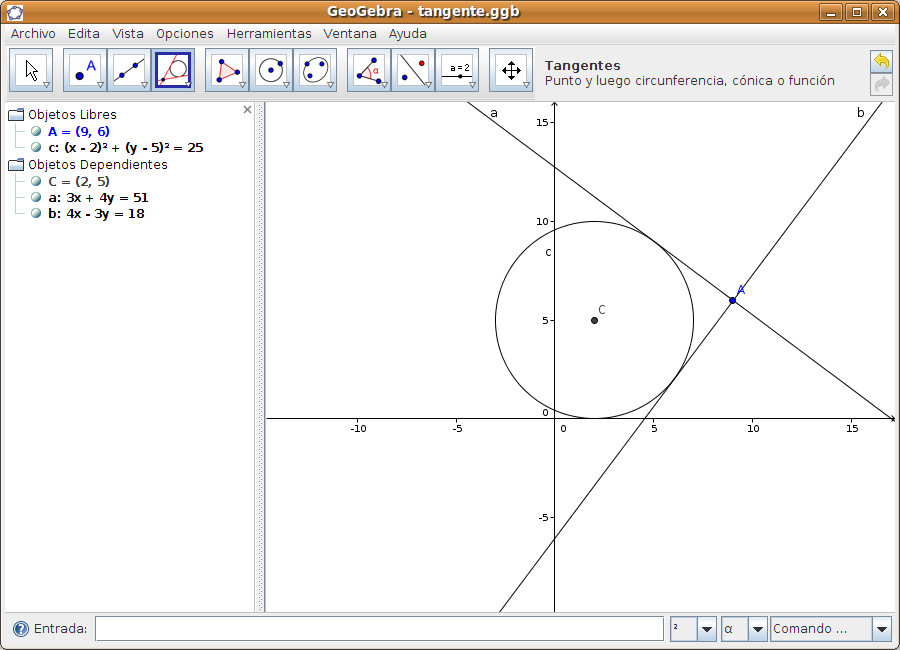
Esperamos unos segundos y se dibujan las dos tangentes, al tiempo que en la zona de álgebra aparecen las ecuaciones de las dos rectas tangentes que se han dibujado.
Paso 4 Utilizamos el botón de desplazamiento En este paso vamos a comprobar como se actualizan las diferentes zonas en función de donde se hagan las variaciones. Por ejemplo, desplazamos la circunferencia y... observamos que las tangentes se adaptan.
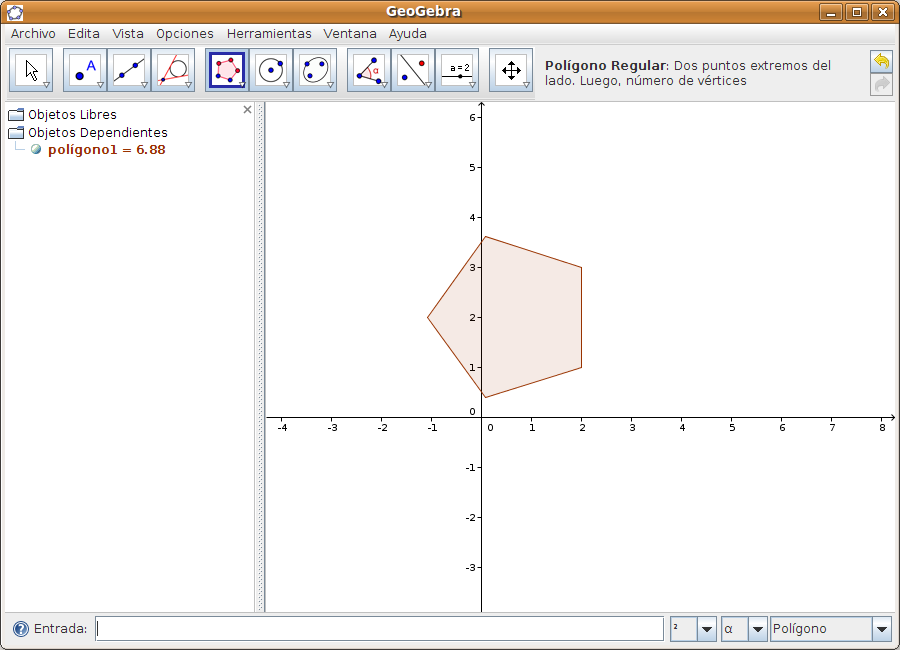
También podemos mover el punto A y comprobar como se mueven las tangentes. Hemos incluido también la barra de reproducción para ver en secuencia los pasos realizados en la construcción. Salvar los cambios si se quieren. Caso 3Vamos ahora a dibujar un pentágono y su circunferencia circunscrita. Paso 1 Dibujamos e pentágono En primer lugar vamos a Archivo > Nuevo para comenzar un nuevo trabajo. En la barra de herramientas seleccionamos el botón Polígono regular En la zona de entradas y comandos, localizamos la orden Polígono. Los datos que requiere esta orden son un punto (a,b) extremo de un lado del polígono, otro punto (a,b) para el otro extremo del lado y el nº de lados del polígono. Los datos dados por nosotros en la fórmula son:
Al pulsar INTRO se dibuja nuestro pentágono.
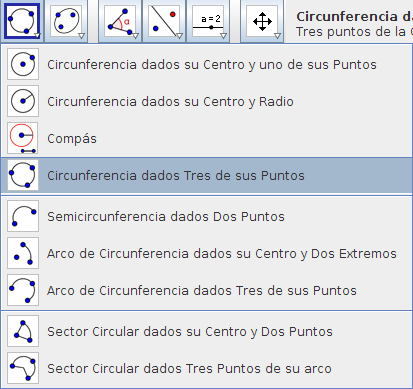
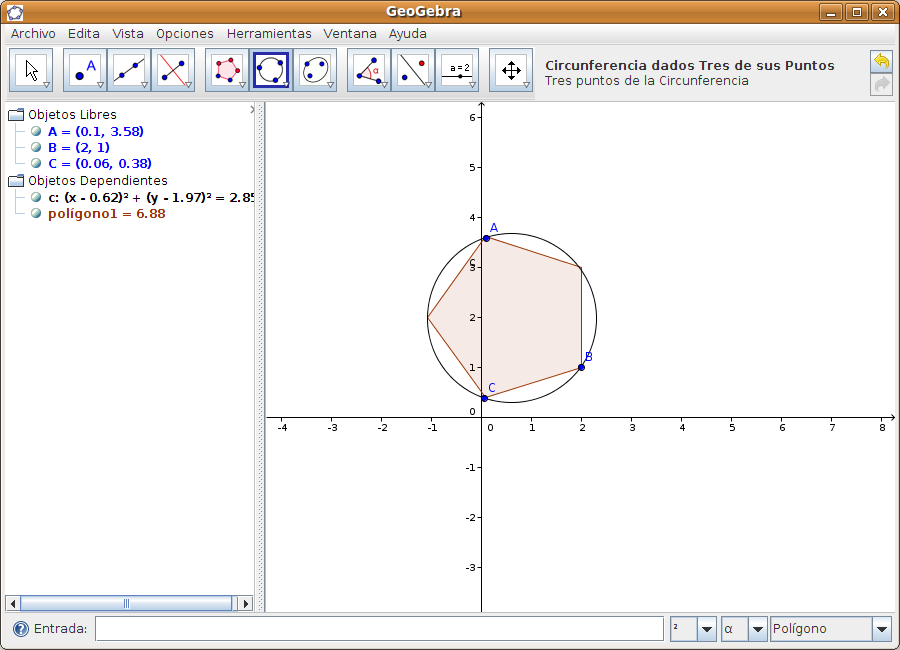
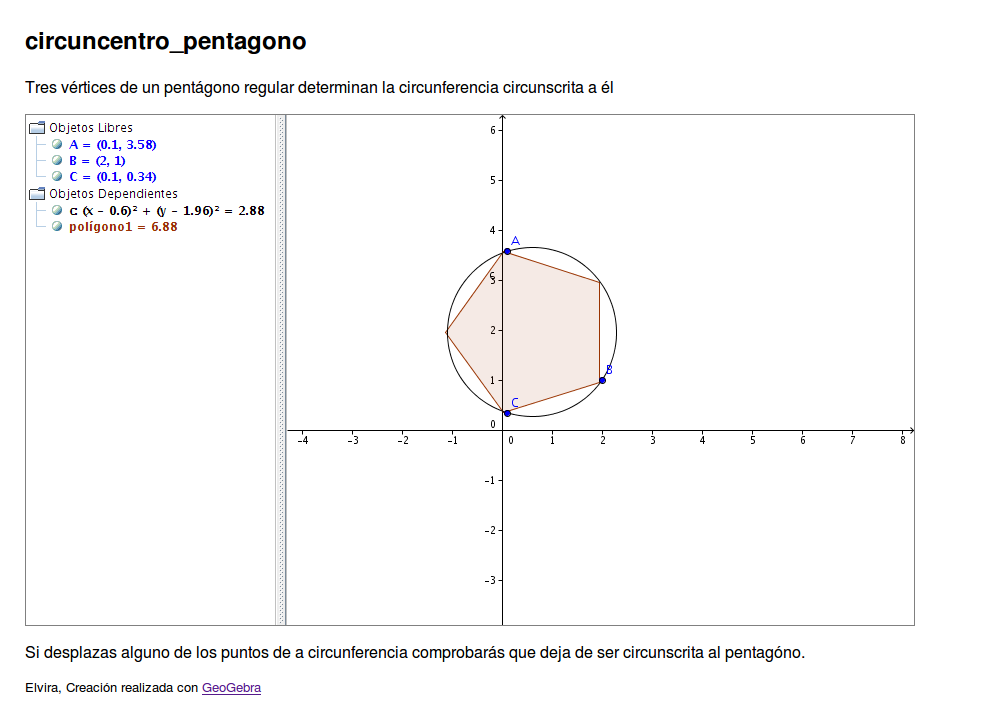
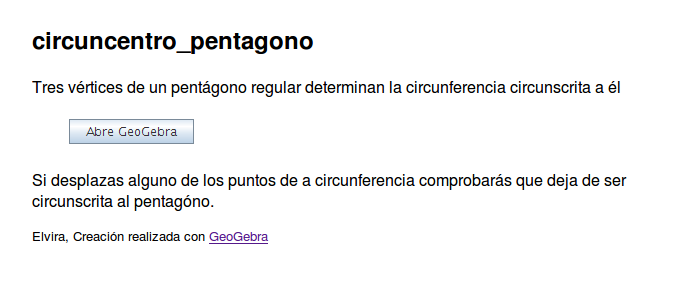
Paso 2 Búsqueda del centro de la circunferencia circunscrita Como se trata de un polígono regular, si tomamos 3 vértices del pentágono, por ellos pasará la circunferencia circunscrita. Buscamos la función correspondiente:
Seleccionamos la opción Circunferencia dados Tres de sus Puntos, y con el ratón marcamos los 3 vértices que queramos. Se dibuja la circunferencia:
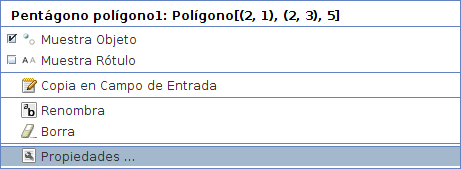
Paso 3 Seleccionamos el modo Desplaza y Esto es lo que llamamos la Geometría dinámica. Todos los objetos tienen sus Propiedades. Para conocerlas estando sobre el objeto, pulsar el botón derecho del ratón y el menú contextual nos muestra:
Seleccionamos la entrada Propiedades y muestra una ventana con propiedades configurables del polígono:
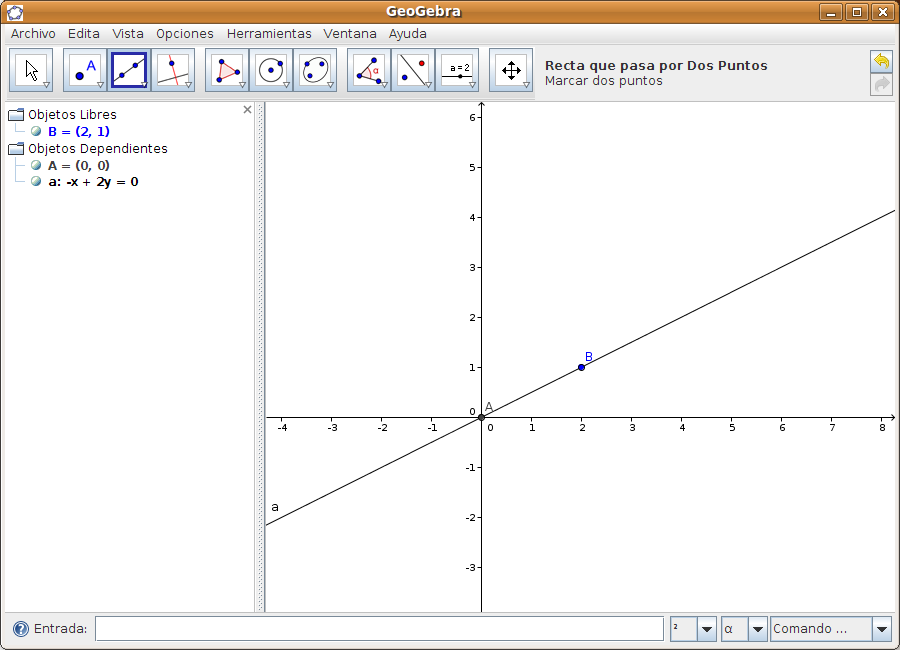
Las diferentes pestañas nos permiten poner subtítulo al objeto, mostrar un rótulo, cambiar los colores, el grosor y estilo del trazo, etc Caso 4 Estudio de funciones lineales f(x)=axPaso 1 Dibujamos una recta que pasa por dos puntos: A(0,0) y B(2,1). Para ello pulsamos en La figura siguiente muestra gráficamente la recta y en la zona de álgebra la ecuación correspondiente:
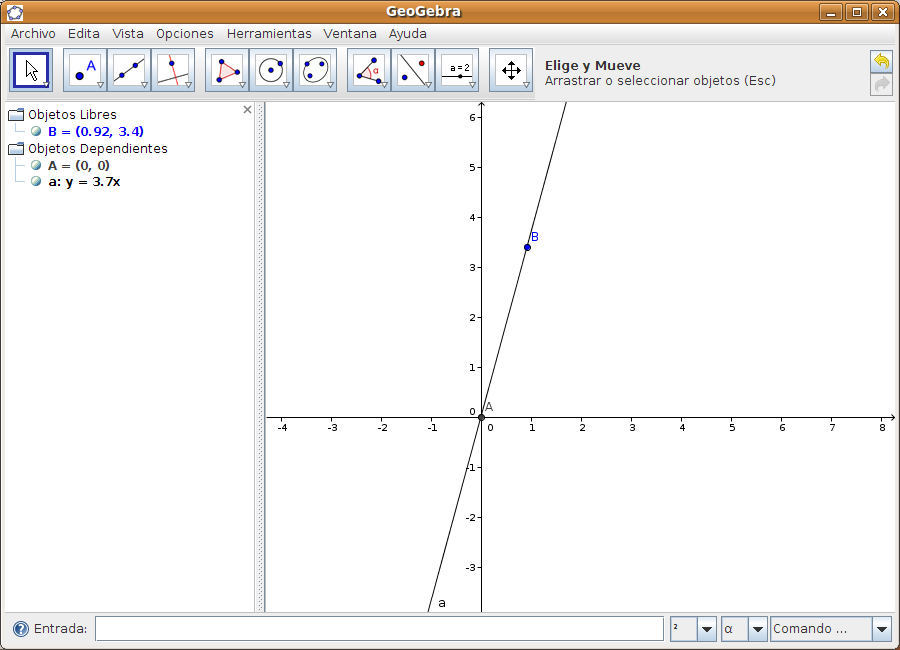
Paso2 Situamos el ratón sobre la recta y en el menú contextual seleccionamos las Propiedades. Vamos a la pestaña Álgebra y cambiamos la ecuación de la recta a y=ax+b para poder estudiar las variaciones en la pendiente de la recta. Si ahora hacemos clic en el botón de desplazamiento y pulsamos sobre el punto B, que es el objeto libre, veremos como cambia la ecuación de la recta al ir cambiando la pendiente de la misma.
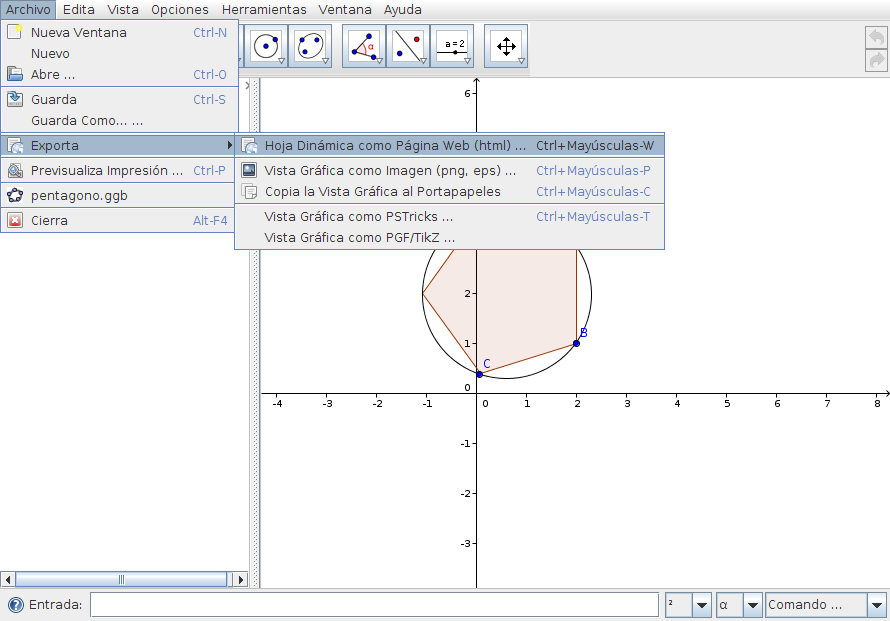
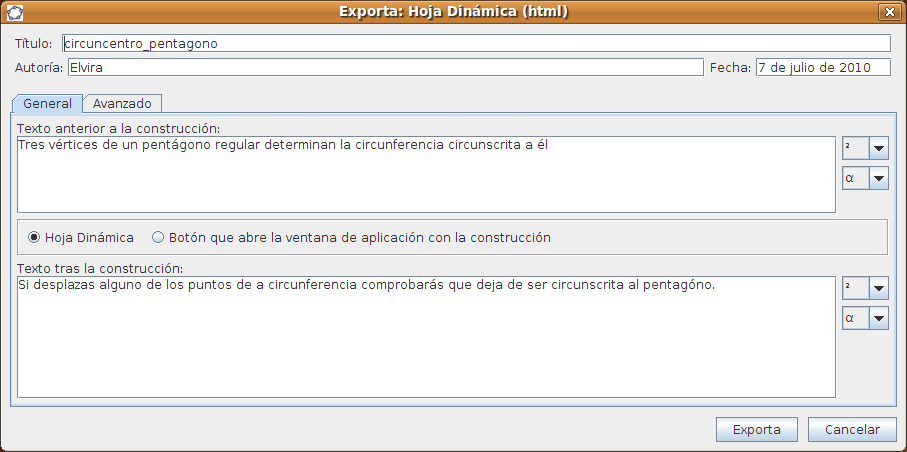
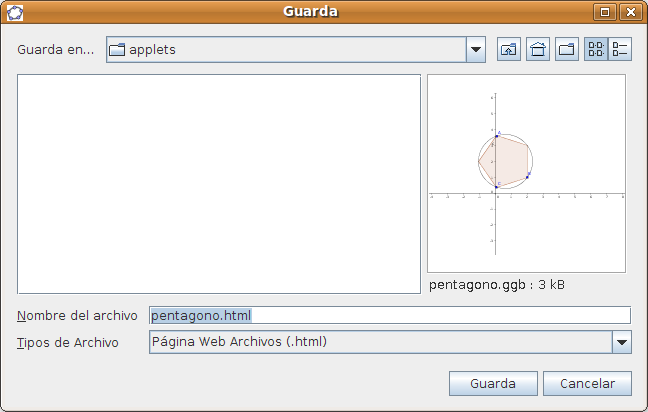
Creación de applets con GeogebraA partir de un dibujo elaborado con Geogebra podemos generar un applet1 que insertaremos en una página web. Elaborar estos dibujos con Geogebra ya hemos visto que es muy sencillo y la generación del applet es automática. Además no pierden la interactividad, como las construcciones que hemos realizado en los casos prácticos. Pasos para crear un appplet con Geogebra
ConclusiónRealmente hemos realizado una descripción muy breve de Geogebra, pero suponemos que se ha podido intuir el potencial que tiene y la gran ayuda que supone para el profesor de Matemáticas interesado en la introducción de las TIC en el aula. Geogebra es mas que un digno rival de Cabri (software educativo y propietario para trabajar con geometría dinámica, http://www.cabri.com/es/) y su difusión es muy grande. Existen numerosas comunidades de usuarios de Geogebra que a través de sus foros, celebración de Jornadas, etc, producen y mantienen numerosa documentación relacionada con el uso de Geogebra en el aula. En concreto desde el ITE (Instituto de Tecnologías Educativas) se ofrece en su sección de Formación en Red, un DVD con experiencias basadas en Geogebra (http://www.isftic.mepsyd.es/formacion/enred/experiencia/index.php) preparadas por los propios profesores que han realizado el curso correspondiente. Enlaces de interés
1En general un applet es un componente de una aplicación que se ejecuta en el contexto de otro programa, por ejemplo un navegador web. En particular el Java applet es código Java utilizado en una página HTML y representado por una pequeña pantalla gráfica dentro de ésta.(http://es.wikipedia.org/wiki/Applet).
|