6.1. Superficies, Curvas y polígonos
En los puntos de las superficies, cada punto puede ser función de dos parámetros, u y v, que varían entre 0 y 1. Veamos cómo utilizarlos para construir una superficie a medida de nuestros deseos en la actividad 6.2. También presentamos, tras explicar la configuración una escena donde se presentan varias superficies:
Éste es el panel de configuración de una superficie.
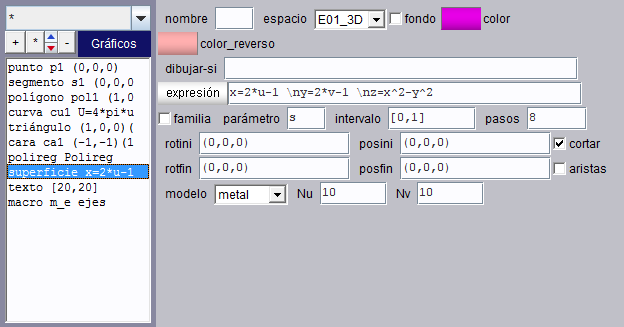
|
expresión |
Es un campo de texto. Su contenido debe tener la forma:
x=X(u,v)
donde X, Y y Z son expresiones numéricas dependientes de los parámetros u y v.
(X(i/Nu,j/Nv),Y(i/Nu,j/Nv),Z(i/Nu,j/Nv)) Antes de x, y, z se pueden definir variables intermedias que sólo se usan para los cálculos que se realizan al dibujar la superficie. |
Podemos incorporar curvas en 3D de forma análoga a como lo hacíamos en dos dimensiones.
Las coordenadas de cada punto de la curva se darán en función de un parámetro: x=x(u); y=y(u); z=z(u). Debemos recordar que, en este applet, los ejes de coordenadas respetan la distribución de la izquierda, en vez de la que poseen en la mayoría de los libros de texto de Enseñanza Secundaria. Desarrollemos un ejemplo concreto a través de la actividad 6.1.
Éste es el panel de configuración de una curva.
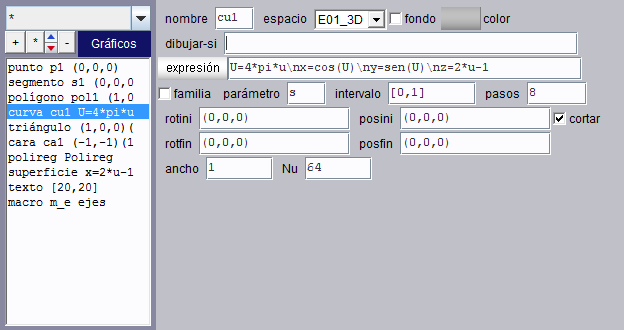
Las curvas se representan paramétricamente y en realidad se dibujan como polígonos.
|
expresión |
Es un campo de texto. Su contenido debe tener la forma:
x=X(u)
donde X, Y y Z son expresiones numéricas dependientes del parámetro u. (X(i/Nu),Y(i/Nu),Z(i/Nu)) para i=0,...,Nu+1. Antes de x, y, z se pueden definir variables intermedias que sólo se usan para los cálculos que se realizan al dibujar la curva. |
|
Nu
|
Campo de texto para definir el número Nu. Las curvas se definen paramétricamente y en ellas se utiliza siempre u como parámetro. Nu es el número de intervalos en los que se parte el segmento unitario [0,1] para dibujar la curva.
Las superficies se definen también en forma paramétrica y se utlilizan los parámetros u y v ambos recorriendo el intervalo unitario [0,1]. Nu es el número de intervalos en los que se parte |
En la siguiente escena se muestra un ejemplo sencillo de la introducción de una curva en un espacio tridimensional.
Aunque se puede lograr a base de curvas y superficies, para dibujar superficies planas es más fácil utilizar polígonos regulares y caras. En la actividad 6.3 aprenderemos a incorporar polígonos regulares, mientras que en la 6.4 crearemos polígonos irregulares. Tras los paneles de configuración se muestra una escena que contiene estos elementos.
Éste es el panel de configuración de un polireg o polígono regular.
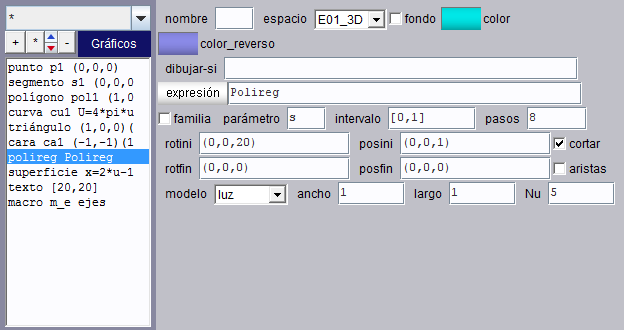
|
expresión
|
Es un campo de texto. Su contenido puede ser cualquier cosa, en realidad este texto sólo se usa como identificador durante la edición. El número de lados del polígono regular queda determinado por Nu y su radio es la mitad de ancho, siempre y cuando ancho=largo. Si ancho#largo entonces el polígono no es regular sino que es una deformación de uno regular. |
|
Nu |
Es un campo de texto. Su contenido es el número de lados del polígono regular. |
|
ancho
|
Es un campo de texto. Su contenido es la mitad del radio del polígono regular de la esfera circunscrita, si ancho=largo. Si ancho#largo entonces el polígono no es regular sino que es una deformación de uno regular. |
|
largo
|
Es un campo de texto. Su contenido es la mitad del radio del polígono regular regular de la esfera circunscrita, si ancho=largo. Si ancho#largo entonces el polígono no es regular sino que es una deformación de uno regular. |
Éste es el panel de configuración de un triángulo.
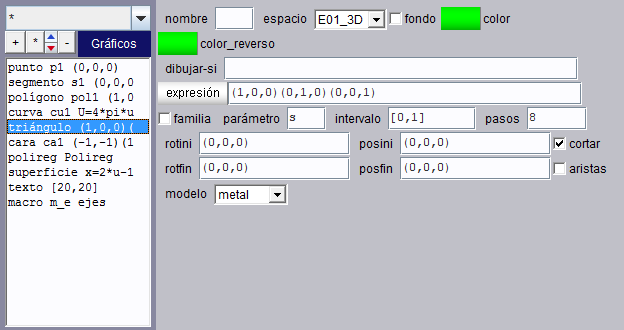
Estos triángulos son superficies en 3-D, es decir tienen dos caras (anverso y reverso), tres aristas, y requieren de una especificación del modo de colorearse.
|
expresión |
Es un campo de texto. Su contenido deben ser las coordenadas de tres puntos del espacio, es decir, una expresión de la forma: (X1,Y1,Z1)(X2,Y2,Z2)(X3,Y3,Z3) donde Xi, Yi, para i=1,2,3 pueden ser expresiones numéricas. |
Nota: En versiones anteriores a Descartes 3.5 era posible crear triángulos y diversos objetos a partir de ellos, pero había que usar el tipo cara con 3 aristas y era complicado colocar a base de translaciones y rotaciones dicha cara en una posición deseada. Los triángulos 3-D en cambio son muy fáciles de construir y es sencillo combinar varios para crear diversos objetos.
Éste es el panel de configuración de una cara.
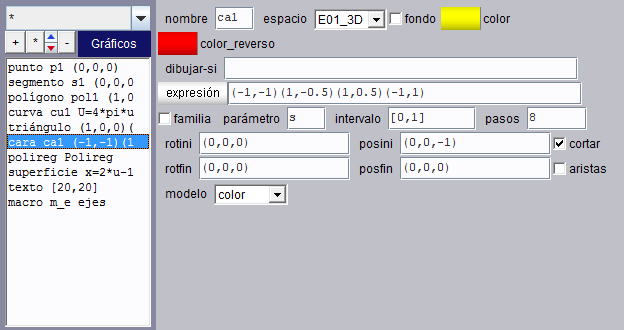
|
expresión |
Es un campo de texto. Su contenido deben ser las coordenadas de un polígono en el plano, es decir, una expresión de la forma: (X1,Y1)(X2,Y2)...(Xn,Yn) donde Xi, Yi, para i=1,...,n son expresiones numéricas. |