| MONOGRÁFICO: Una calculadora gráfica para la enseñanza de las matemáticas |
 |
 |
 |
| SOFTWARE - Software educativo |
| Écrit par Luis González |
| Dimanche, 29 Juillet 2012 07:55 |
|
There are no translations available.
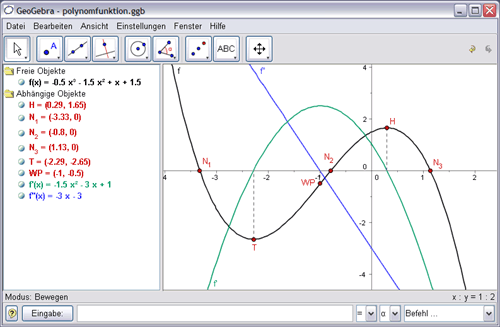
Dentro del currículo de contenidos mínimos para el Bachillerato en la modalidad de Ciencias Sociales, los estudiantes tienen que cursar la asignatura de Matemáticas Aplicadas a las Ciencias Sociales II, uno de cuyos contenidos, dentro del bloque dedicado al Álgebra, es la programación lineal, así como sus aplicaciones a la resolución de problemas sociales, económicos y demográficos, y la interpretación de sus soluciones. IntroducciónEl problema que los alumnos deben saber resolver, aplicar e interpretar consiste, pues en maximizar una función lineal de dos variables con un dominio definido por inecuaciones en las cuales sólo aparecen, a lo sumo, las dos variables que definen la función. Aunque las inecuaciones se han estudiado en cursos anteriores (al menos en una variable), la interpretación gráfica requiere, al pasar a dos dimensiones, un esfuerzo adicional por parte de los estudiantes. Y la comprensión, y la justificación, del procedimiento gráfico que habitualmente se les propone para resolver los problemas de programación lineal es difícil empleando métodos tradicionales, e incluso inaccesible si dichos métodos se reducen al cálculo puramente algebraico de la solución. En ocasiones se dejan en el tintero cuestiones teóricas sumamente interesantes, relativas a este punto del temario, debido a restricciones de tiempo, que se emplea en resolver algebraicamente ejercicios del mismo tipo, obviando que es muy deseable desarrollar las habilidades necesarias para interpretar una situación gráficamente y para ser capaz de resolverla algebraicamente simultáneamente, pero que también es posible trabajarlas de forma asíncrona. El uso de las nuevas tecnologías permite, precisamente, que la representación gráfica de muchos conceptos matemáticos, y en particular de los que están implícitos en la formulación y resolución de los problemas de optimización lineal, no dependa de la pericia ni de la rapidez con que se realicen los cálculos algebraicos. En segundo lugar, recopilamos y analizamos parte del software a disposición del profesor y estudiante para representar gráficamente los problemas de optimización lineal. En tercer lugar, mostramos una calculadora gráfica diseñada específicamente para ser utilizada por profesores y estudiantes en el tema dedicado a la programación lineal, mostrando sus características técnicas y didácticas. Por último, establecemos unas conclusiones sobre posibles mejoras y desarrollos futuros de dicha herramienta. La enseñanza de las matemáticas y las nuevas tecnologíasDesde que los institutos públicos españoles comenzaron a disponer de los primeros ordenadores en el aula, hace más de veinticinco años, hasta hoy, ha tenido lugar una profunda transformación de todos los protagonistas de lo que se conoce como tecnologías de la información y la comunicación (TIC) aplicadas a la enseñanza. Han evolucionado las máquinas, el modo en que acceden y presentan la información, su aspecto externo, su tamaño, su peso, su portabilidad, su precio, etc. Paralelamente, ha cambiado el perfil de los usuarios de dichas máquinas (hay más, y más experimentados y motivados, especialmente entre los jóvenes, que han crecido con Internet, el teléfono móvil y el ordenador portátil) y, como no, la actitud de las propias instituciones educativas con respecto al papel que las TIC deben jugar en la formación de los estudiantes, en todos los niveles de la educación, situándose en el centro de las políticas públicas educativas en los países occidentales, en Europa y, más en particular, en España. El aprendizaje basado en competencias actualmente vigente en España estipula que una de las competencias básicas que el alumno debe adquirir con la educación obligatoria es la denominada competencia digital (y de tratamiento de la información), que se define como consistente en “utilizar las tecnologías de la información y la comunicación extrayendo su máximo rendimiento a partir de la comprensión de la naturaleza y modo de operar de los sistemas tecnológicos, y del efecto que esos cambios tienen en el mundo personal y sociolaboral. Asimismo supone manejar estrategias para identificar y resolver los problemas habituales de software y hardware que vayan surgiendo. Igualmente permite aprovechar la información que proporcionan y analizarla de forma crítica mediante el trabajo personal autónomo y el trabajo colaborativo, tanto en su vertiente sincrónica como diacrónica, conociendo y relacionándose con entornos físicos y sociales cada vez más amplios. Además de utilizarlas como herramienta para organizar la información, procesarla y orientarla para conseguir objetivos y fines de aprendizaje, trabajo y ocio previamente establecidos. En definitiva, la competencia digital comporta hacer uso habitual de los recursos tecnológicos disponibles para resolver problemas reales de modo eficiente. Al mismo tiempo, posibilita evaluar y seleccionar nuevas fuentes de información e innovaciones tecnológicas a medida que van apareciendo, en función de su utilidad para acometer tareas u objetivos específicos. [...]” (Real Decreto 1631/2006, de 29 de diciembre, por el que se establecen las enseñanzas mínimas correspondientes a la Enseñanza Secundaria Obligatoria). Los nativos digitales que habitan las escuelas de hoy cumplen con creces una buena parte de los múltiples objetivos que implica la definición precedente (por ejemplo, la correspondiente a la actualización de sus conocimientos técnicos), y el verdadero reto para la institución educativa está entonces en orientar el buen uso de las TIC que el alumno ya utiliza, además de asimilar en sus programas adecuadamente todas las potencialidades que tiene a su alcance. La competencia matemática es, también, una de las ocho competencias básicas que marca la ley. Matemáticas y TIC han tenido, mucho antes de que los ordenadores llegasen a las escuelas de enseñanza media, una relación sumamente estrecha. Básicamente, puede resumirse en una frase: los ordenadores se convirtieron, en un primer momento, en el laboratorio del que carecía el matemático profesional, en las más insospechadas ramas (en el Análisis, en la Geometría, ¿quién lo iba a decir?); y, en una segunda fase, en un medio para distribuir la información, como ocurrió en casi todos los ámbitos científicos. Esto es posible gracias a que el ordenador permite llevar a cabo dos funciones que la investigación matemática utiliza como cualquier otra ciencia, en un tiempo que antes de su aparición era impracticable: la autoevaluación de conjeturas y la experimentación. Estas dos funciones, autoevaluación y experimación, son comunes a la práctica investigadora y al aprendizaje de las matemáticas (al fin y al cabo, ¿qué es un estudiante de matemáticas sino un matemático investigando, eso sí, lo que ya ha sido descubierto?). Cuando el alumno utiliza el ordenador para realizar los cálculos precisos, pero mucho más ágilmente y con mucha más fiabilidad que si los realizase con papel y lápiz, podemos decir que estamos usándolo como calculadora, y viene al caso el excelente artículo The Algebraic Calculator as a Pedagogical Tool for Teaching Mathematics, del profesor Berhard Kutzler, en el que presenta la “espiral de creatividad de Buchberger”, y que describe así: “Applying known algorithms produces examples. From the examples, we obtain properties, which are expressed as a conjecture. Proving the conjecture yields a theorem, i.e., guaranteed knowledge. The theorem’s algorithmically usable knowledge is implemented in a new algorithm. Then, algorithm is applied to new data, yielding new examples, which lead to new observations, … “ [KUTZLER]. Esta es la vieja teoría didáctica de Ives Chevallard virtuosamente emparejada con el uso de las calculadoras (u ordenadores utilizados como calculadoras). En el fondo, lo que se propone es el uso de la calculadora como herramienta que permita abstraer la parte interesante del quehacer matemático (establecimiento de conjeturas, análisis de resultados y prueba de teoremas) de la rutinaria, que puede ser encargada a la calculadora. En el ámbito escolar, pues, la espiral de Buchberger equivale a un andamiaje (scaffolding en inglés), que es “any pedagogically justified sequence of using an not using technology for trivialization, experimentation, visualization or concentration either in the sense of automation or compensation” [KUTZLER]; es decir, se trata de ofrecer al alumno una calculadora que le permita experimentar, concentrar su esfuerzo en las tareas importantes de lo que se traiga entre manos, trivializando tareas secundarias, y visualizar en el acto sus propias intuiciones, todo ello en los momentos adecuados. Por supuesto, el uso de calculadoras debe ser limitado (no debe sustituir la habilidad del alumno para realizar los mismos cálculos sin el soporte informático) y coherente (si se usa cotidianamente en el aula, habría que plantearse su uso en los momentos de evaluación). Consideramos que una calculadora que permita representar los problemas clásicos de la programación lineal es, por todo lo comentado, sumamente interesante. Software para la enseñanza de la programación linealExisten muchas herramientas y materiales didácticos disponibles para ser utilizadas en el tema de la programación lineal de Bachillerato de Ciencias Sociales. Sin pretender ser exhaustivos, vamos a repasar las características de algunos de ellos. El software a disposición de los institutos, profesores y alumnos, puede clasificarse de muchas maneras. Una clasificación útil es la que divide los programas disponibles en programas de propósito general y programas de propósito específico. Con la vista puesta en el aprendizaje de algún punto del currículo, podemos considerar como software de propósito específico aquel que está especialmente diseñado para ser utilizado en un único momento del itinerario curricular (por ejemplo, en el tema de la programación lineal); el software de propósito general sería aquel que puede ser utilizado dentro de los límites de una unidad didáctica, pero que puede ser reutilizado en el aprendizaje de otros temas. Por lo general, el software de propósito general requerirá, tanto para el alumno como para el profesor, un aprendizaje previo para interactuar con el programa, que es un coste adicional al que supone la interacción con la máquina, mientras que el de propósito específico, puesto que en general tendrá una funcionalidad restringida, requerirá un aprendizaje menor, o incluso ningún aprendizaje previo. Microsoft ExcellCon esta distinción in mente, y con esta caracterización de cada uno de los tipos de software, podemos citar como software de propósito general la hoja de cálculo de Microsoft, Excel, que cuenta con un complemento denominado Solver, que permite calcular la solución al problema de programación lineal general (utilizando diversos algoritmos); y, por supuesto, programas de geometría dinámica como Geogebra, que pueden ser utilizados para resolver problemas de programación en dimensión n = 2.
La hoja de cálculo Excel, que tiene grandes ventajas para cubrir diferentes puntos del currículo de matemáticas en distintos niveles de la enseñanza, resulta algo alambicada cuando se quiere aplicar a la programación lineal de segundo de Bachillerato de Ciencias Sociales. Aparte, por supuesto, de la desventaja que supone el hecho de que Excel no es un software gratuito (y que, por consiguiente, no se puede esperar que los alumnos puedan usarlo fuera del ámbito escolar, si es que la escuela posee licencia de uso), su uso requiere un aprendizaje previo del manejo de la hoja de cálculo y, si ya se tiene, del complemento que sirve para resolver este tipo de problemas. Existen experiencias documentadas del uso de Excel como herramienta tecnológica para explicar la programación lineal, con “resultados prometedores para muchos docentes que han seguido la prueba y pueden ser también camino de esperanza para otros compañeros” [PRIETO], según los autores. GeogebraAl contrario que Excel, Geogebra es gratuito y está disponible en red, de modo que no es necesario instalarlo en los equipos antes de que se vaya a utilizar (esta última puede parecer una ventaja menor, pero hay que tener en cuenta lo comentado en el primer apartado de este trabajo sobre las razones que llevan a los profesores de secundaria a mostrarse reticentes al empleo en sus clases de las herramientas tecnológicas). En relación al tema de la programación lineal, puede emplearse para calcular las soluciones de un problema en dimensión n = 2, pero es necesaria cierta inversión de tiempo en aprender a manejar el programa. Permite cierto grado de andamiaje para calcular la solución de problemas concretos (en el sentido de que Geogebra realiza parte de los cálculos algebraicos necesarios para llegar a ella), pero no dispone de objetos específicos para programación lineal, de manera que el estudiante que utilice directamente el programa como apoyo en sus cálculos debe dominar ya la técnica de resolución gráfica (y no puede, por tanto, ser utilizado como “andamio” para actividades más conceptuales para aquellos alumnos que no dominan dicha técnica suficientemente).
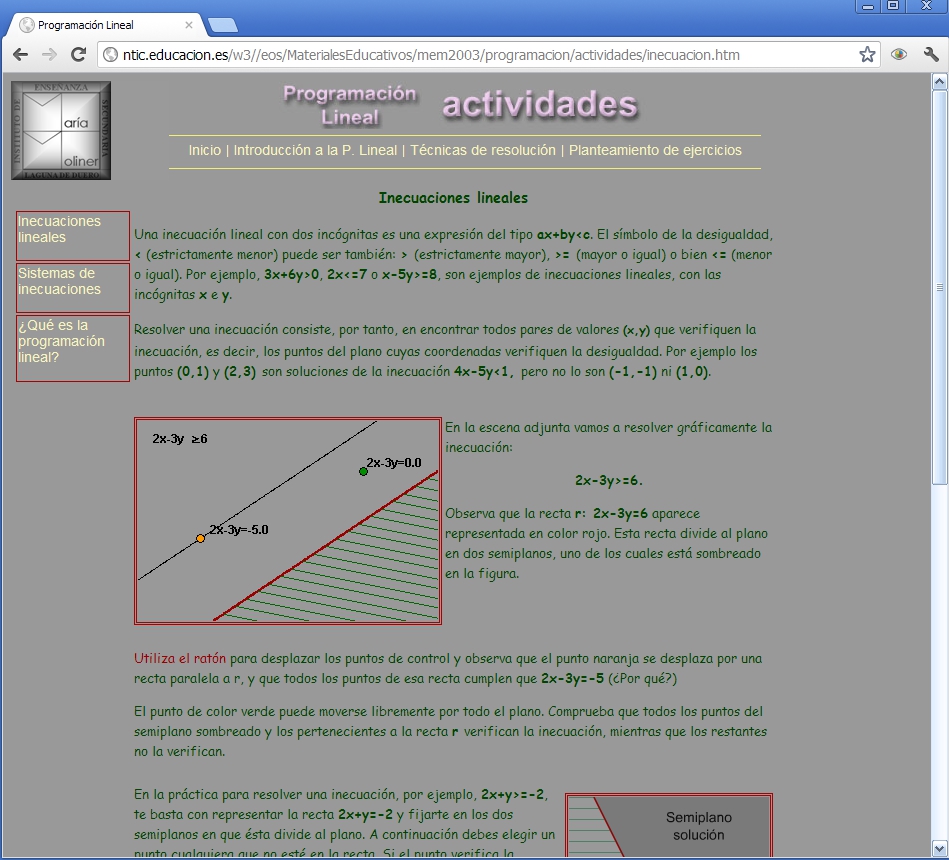
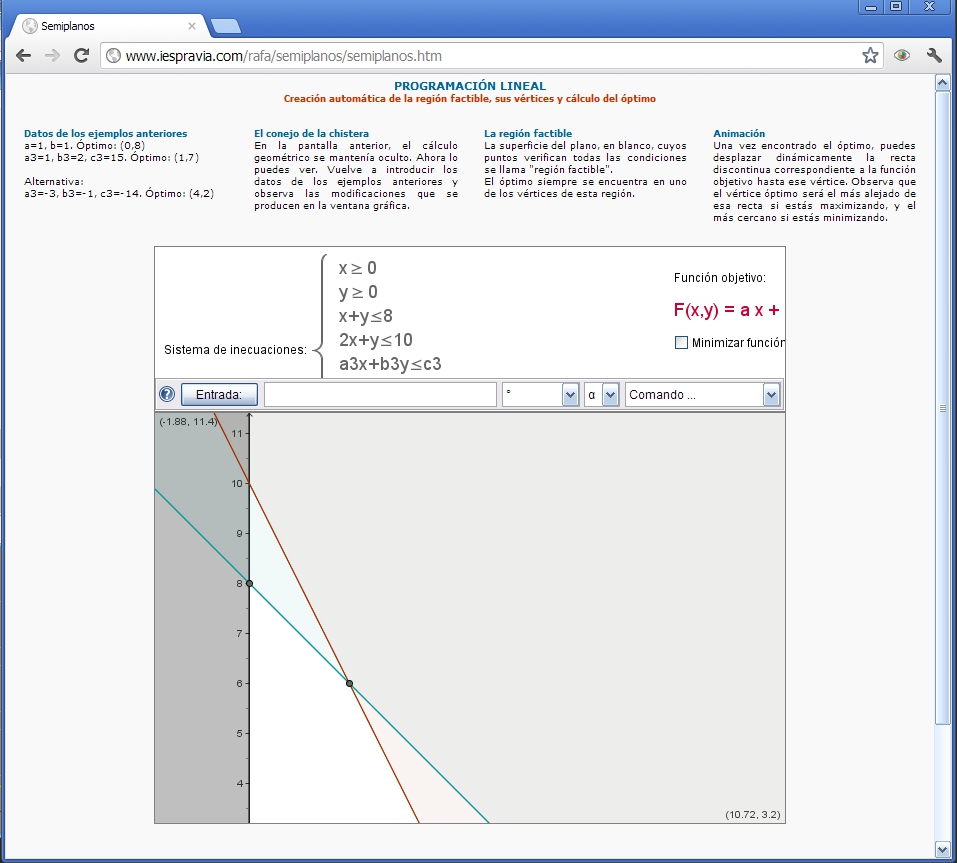
En cuanto a software específico adecuado para estudiar la programación lineal, tal y como se estudia en el Bachillerato de Ciencias Sociales, existen múltiples materiales en Internet con los que trabajar los registros gráfico y algebraico relativos a las inecuaciones lineales con dos variables, pero no hemos hallado gran cantidad de material para el cálculo o representación de los problemas de programación lineal planos. Entre los que están basados en Geogebra, más orientados al estudio de los conceptos algebraicos subyacentes a la programación lineal que a la resolución del problema en sí, existe gran cantidad de páginas web en Internet. Destacamos las siguientes: La primera de ellas contiene gran cantidad de excelente material, tanto para profesores como para alumnos, así como actividades de todo tipo realizadas con Geogebra, pero se aleja del concepto de “calculadora gráfica”, ya que sólo permite representar la región factible. La página del INTEF, por su lado, ofrece diversas actividades interactivas y un ejemplo interactivo de cálculo del óptimo, pero está también bastante alejada en su concepción del concepto de calculadora gráfica, por una razón parecida.
La tercera de las páginas, del profesor Rafael Losada, contiene, junto con las actividades interactivas correspondientes, una construcción en Geogebra que sirve exactamente para resolver algunos problemas de programación lineal en dimensión n = 2. Es un material excelente, aunque no permite la representación de regiones factibles generales.
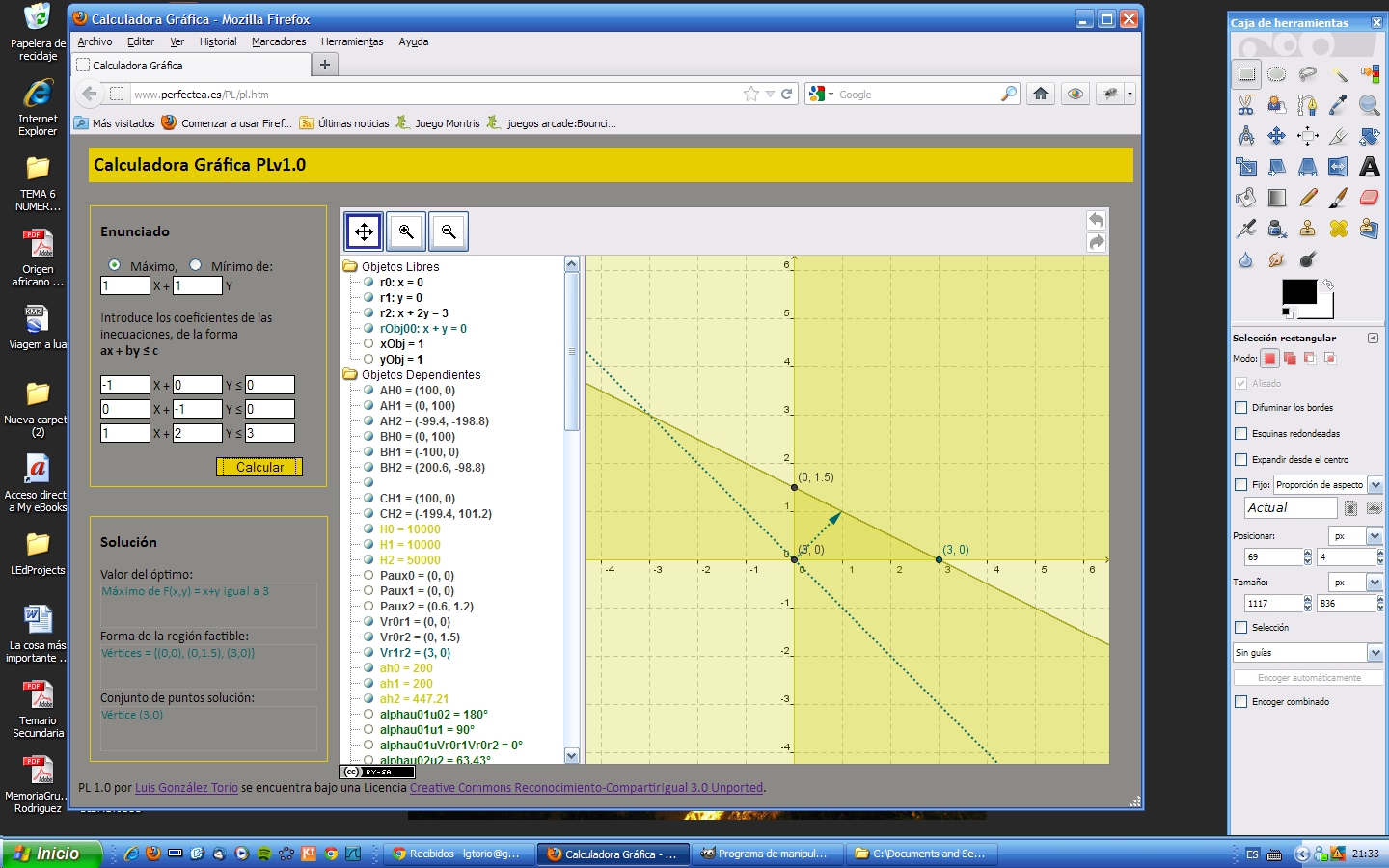
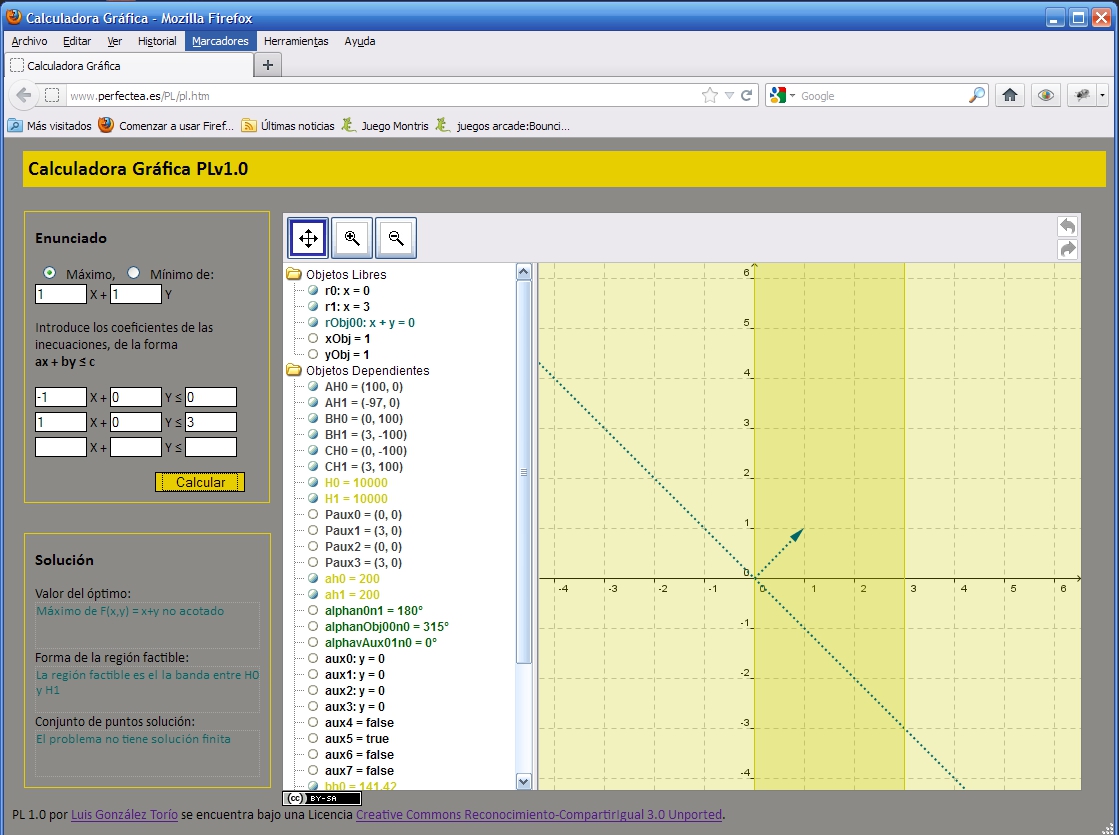
La calculadora gráfica PL (v 1.0)PL es un prototipo de calculadora gráfica y algebraica pensada para resolver problemas de programación lineal en dimensión 2. Está disponible en la siguiente dirección web: http://www.perfectea.es/PL/PL.htm y tiene licencia Creative Commons (Reconocimiento, Compartir igual). Su autor es el de este monográfico. El prototipo acepta regiones factibles definidas con un número de inecuaciones menor o igual a tres, y calcula el máximo o el mínimo de la correspondiente función objetivo gráficamente, detallando también las características de la región factible y el conjunto solución, cuando existe, tanto gráfica como analíticamente (explicitando las causas de la inexistencia de soluciones en cada caso correspondiente). Los siguientes ejemplos gráficos muestran distintos tipos de situaciones que, normalmente, quedan fuera del estudio que se hace en las aulas, debido a que la región factible presenta anomalías. (Y en todo caso, recomendamos utilizar la herramienta para comprobar posibilidades alternativas.)
Pantallazo - PL - region factible acotada unica solucion
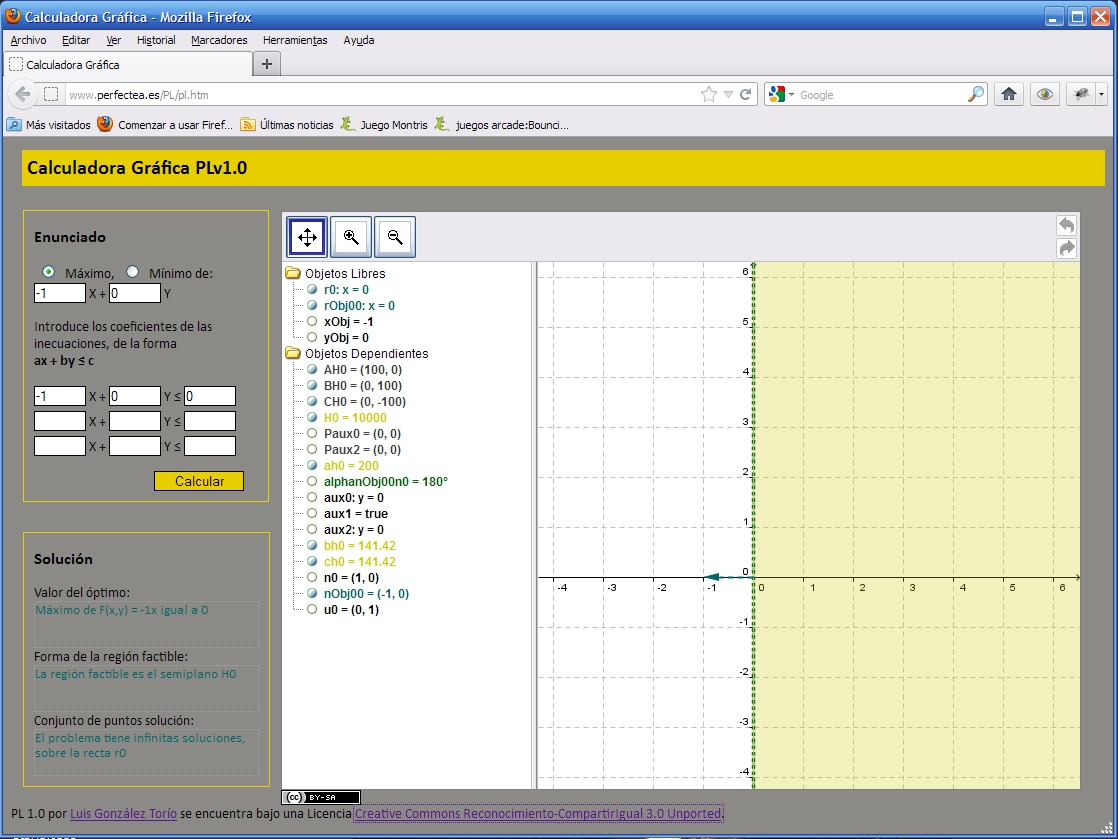
Pantallazo - PL - region factible no acotada infinitas soluciones
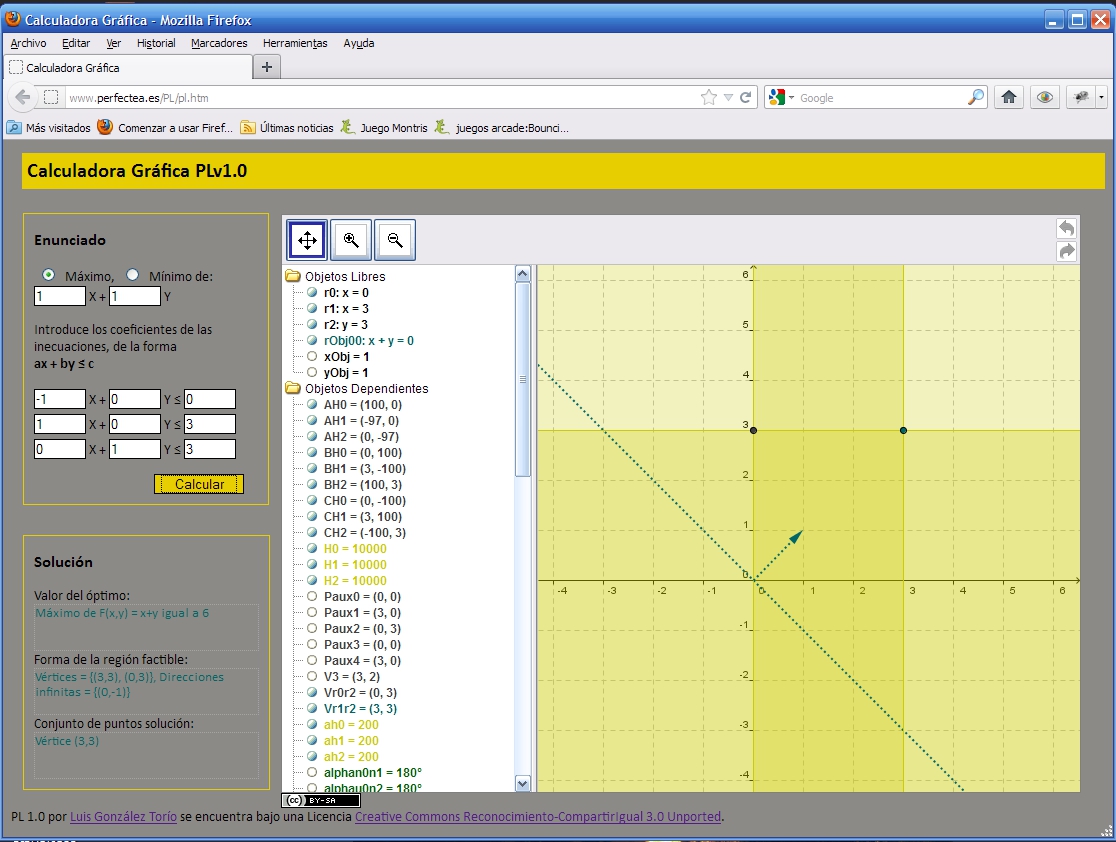
Pantallazo - PL - region factible no acotada unica solucion
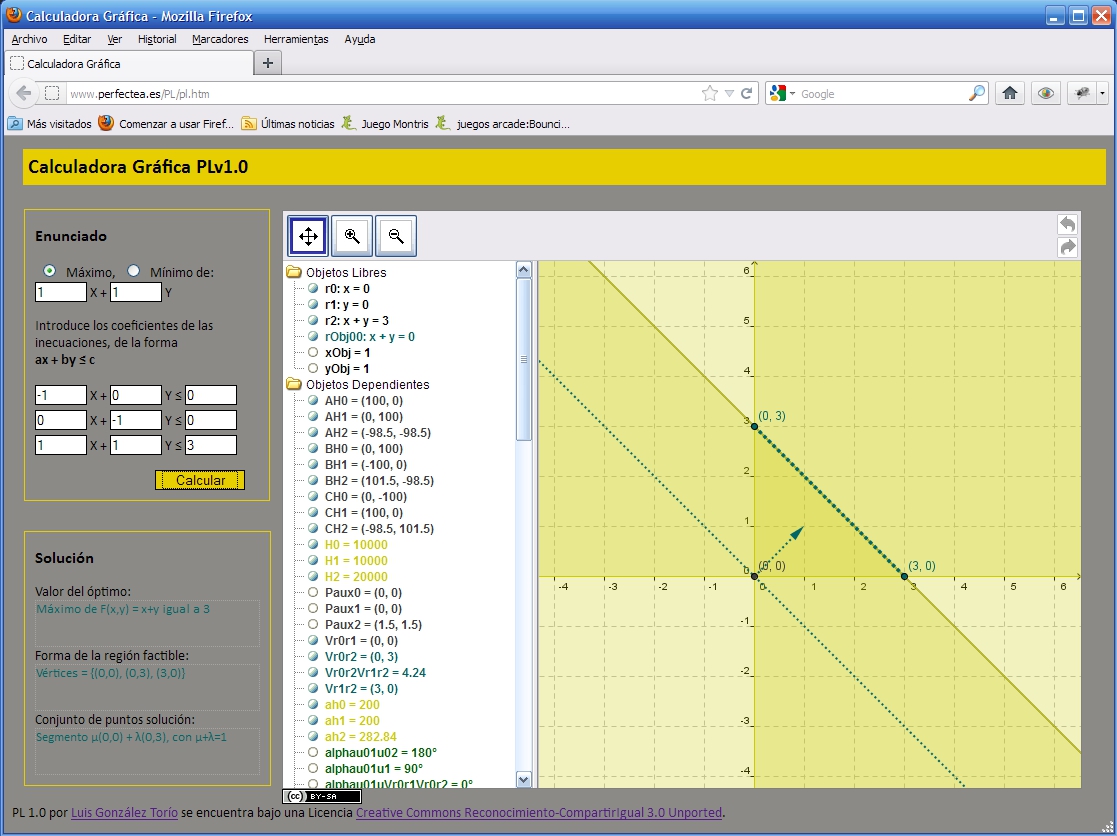
Pantallazo -PL - region factible acotada infinitas soluciones
Pantallazo -PL -region factible no acotada sin solucionj Está diseñado con una interfaz web, que consta fundamentalmente de 3 partes o “ventanas” bien definidas: una primera en la que se introducen los datos del problema a resolver (ventana “Enunciado”), una segunda ventana (ventana “Solución”) donde pueden leerse los datos relativos a la solución del problema, una vez que se ha calculado (óptimo, forma de la región factible y del conjunto de lo soluciones), y una tercera ventana gráfica, donde se muestra la representación gráfica de la solución (ver ilustración 1 del anexo). La ventana gráfica es una ventana abierta por un applet de Geogebra. De hecho, la solución construida por PL es lo que podría llamarse una “pseudoconstrucción” en Geogebra, en el sentido de que todos los cálculos matemáticos que realiza el programa están realizados utilizando Geogebra, aunque el algoritmo utilizado para encontrar la solución está programado en JavaScript. Como resultado, aunque la solución se obtiene mediante una construcción completamente realizada dentro del programa de geometría dinámica, no se garantiza que dicha solución sea resistente a variaciones dinámicas de los objetos libres que la definen, razón por la cual no se ha habilitado más interacción con la ventana gráfica que la necesaria para centrar, mediante movimiento de los ejes y cambio de escala, el dibujo que da lugar a la solución. Por supuesto, sería deseable una construcción de la solución tal que pudiera interactuarse gráficamente con la misma, aprovechando así todas las características propias del software de geometría dinámica. Dicha construcción es posible (y está realizada) si se restringe la forma de la región factible, aunque una única construcción resistente a cualquier variación de los objetos que definen la región factible ha sido imposible de obtener. Por consiguiente, si se desea utilizar la calculadora PL para trabajar la alternancia de registros analítico y gráfico, en el sentido del segundo al primero, debe ser utilizada estableciendo conjeturas acerca de qué inecuaciones definirán regiones con cierta forma que sean comprobadas después, o relegar directamente PL en favor de otro tipo de herramientas más adecuadas a este fin. Conclusiones y bibliografíaConclusionesSi bien existe material didáctico basado en las TIC de gran calidad que puede emplearse para mejorar la enseñanza y aprendizaje de algunos puntos relativos a la programación lineal (estudio de la solución de sistemas de inecuaciones en dos variables, posición relativa de rectas planas e hiperplanos que éstas definen, etc.), no existen muchas herramientas que permitan automatizar el cálculo gráfico y algebraico de un problema típico de programación lineal, concebido como una calculadora, y que permita realizar un andamiaje interesante para esta parte del currículo del Bachillerato. Una calculadora del tipo PL tiene, por el contrario, todas las ventajas de una calculadora gráfica que hemos señalado anteriormente: permite la trivialización, visualización, concentración, experimentación y autoevaluación, y de abordar problemas conceptuales más complejos cuando quizás no se dominan del todo las técnicas básicas empleando la técnica del scaffolding. El profesor puede integrar fácilmente PL en sus clases, sin necesidad de reestructurar metodológicamente sus clases, y empleando material didáctico “clásico”, e incluso puede utilizar PL como herramienta para realizar presentaciones, si dispone de proyector o pizarra digital. Por tratarse de una aplicación web, no requiere instalación previa, ni requiere el aprendizaje (ni para el alumno, ni para el profesor) de ningún tipo de habilidades especiales con el ordenador o de manejo de software, lo que supone un ahorro real de tiempo y esfuerzo. Esta versión cuenta con serias limitaciones, también: sólo permite calcular la solución para problemas con región factible definida por tres inecuaciones, el alumno no puede interactuar con la ventana gráfica (más que para acercar o alejar la construcción), y no puede utilizarse en dispositivos del tamaño de una calculadora gráfica al uso. De hecho, las mejoras y posibles desarrollos para la herramienta pasarían por eliminar estas limitaciones: generalizar la región factible a un número indefinido de inecuaciones, realizar una construcción verdaderamente dinámica (de forma que se pueda interactuar con la pantalla gráfica) y, quizás, obtener una versión para dispositivos móviles. Bibliografía
|