| Graph III |
 |
 |
 |
| SOFTWARE - Software educativo | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Astelehena, 2008(e)ko maiatza(r)en 26-(e)an 15:49etan | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
There are no translations available. Descubre a través de este tutorial esta sencilla herramienta para dibujar gráficas... Graph III (Creación de gráficas)7. Estudio de ecuaciones de segundo gradoHemos visto hasta ahora la representación y estudio de las funciones más simples: constantes y rectas. Ampliemos nuestro conocimiento con el estudio de funciones con polinomios de segundo grado. Toda función con polinomio de segundo grado es de la forma: Asociada a toda función de este tipo existe una ecuación de segundo grado:
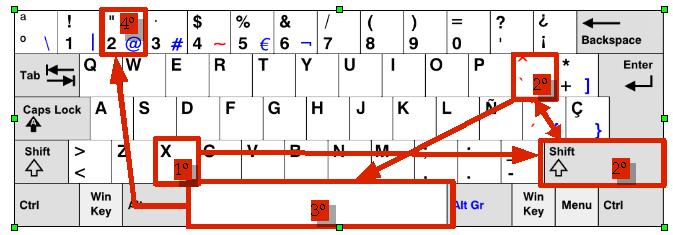
Vamos a estudiar los cuatro apartados más adelante haciendo un ejemplo concreto de cada uno. Pero antes de seguir, lo primero que debemos tener en cuenta es la forma en que tendremos que escribir esta función en nuestro programa. Ese x elevado a 2 tal y como aparece en la ecuación no es posible insertarlo directamente en la casilla Ecuación de la función de la ventana Insertar ecuación. La forma de escribir x elevado a 2 se hace pulsando en el orden que se indican las siguientes teclas: la de x, luego a la vez la de mayúsculas y la del acento circunflejo ^ , despué
Si hemos hecho estos pasos nos aparecerá reflejado en la casilla x^2.
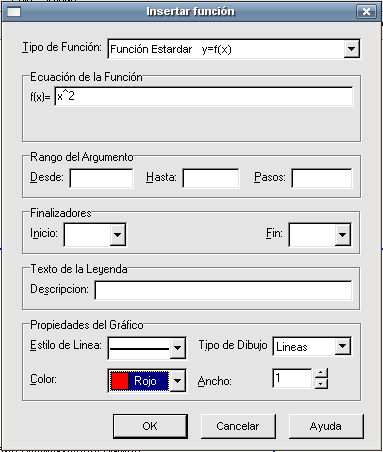
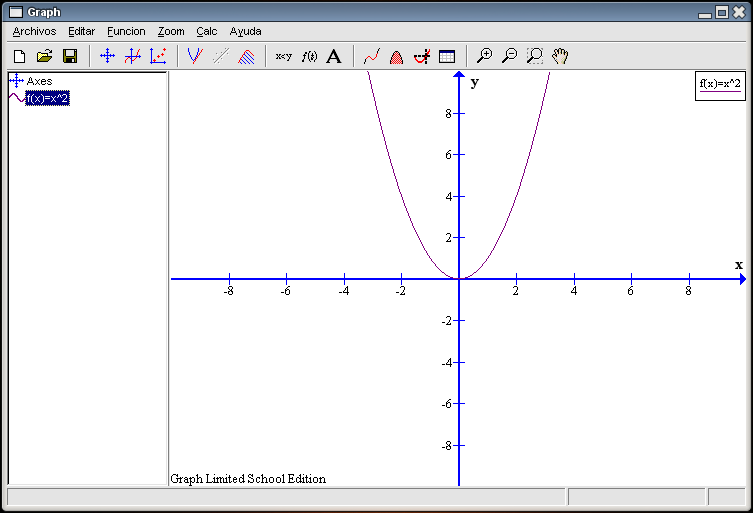
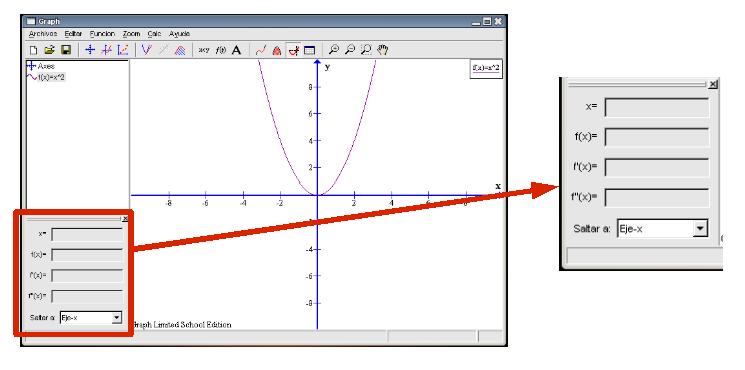
Caso ax2=0Empezaremos con el caso más sencillo de este tipo haciendo que a = 1, por lo que la función tendrá esta forma Creemos una nuevo archivo y al igual que hicimos en ejercicios anteriores para crear esta función, pulsemos en el botón Insertar una nueva función (el quinto por la izquierda de la barra de herramientas) para indicar la ecuación (tal y como hemos visto en la página anterior). Tras pulsar en OK la gráfica será así:
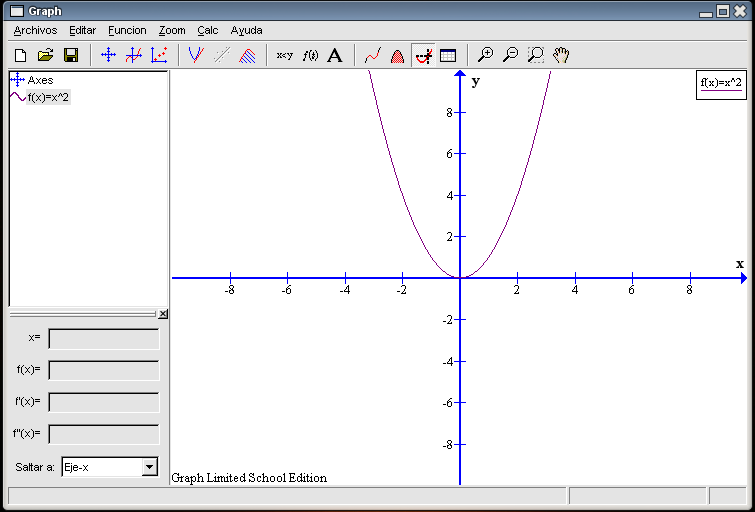
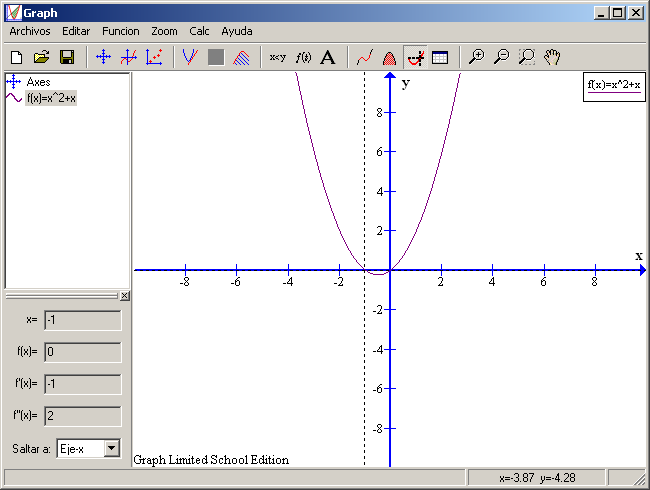
El valor (el punto) que deseamos calcular, y fijándonos en la gráfica, coincide con la intersección del trazado de la función y los ejes de coordenadas. Estos cortes sí que somos capaces de averiguarlos usando las herramientas de que dispone el programa y que hemos visto en casos anteriores. Seleccionamos de la barra de herramientas el botón Evaluar la función seleccionada y elegimos del recuadro inferior izquierdo la opción Eje-x ¿Sale reflejado algún valor? No, las casillas se quedan en blanco. Es un fallo del programa.
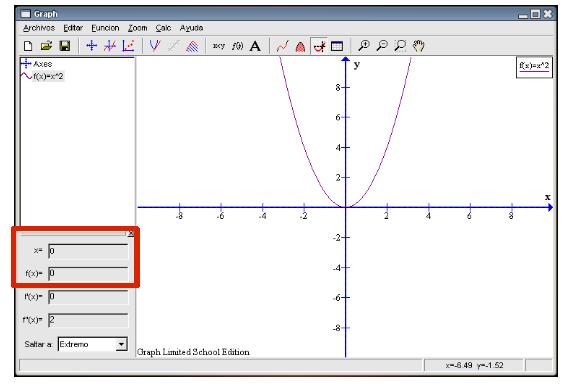
¿Qué podemos hacer? Dejamos pendiente del apartado dedicado a rectas una opción en el recuadro inferior izquierdo llamada Extremo. Ésta nos averigua los posibles mínimos y máximos de la función que estemos estudiando. Procedamos a utilizarla. Teniendo seleccionado de la barra de herramientas el botón Evaluar la función seleccionada, elegimos del recuadro inferior izquierdo la opción Extremo ¿Nos aparece algún valor? Sí, en este caso aparece el punto (0 , 0) como el lugar en que la función toma su mínimo.
Esta es la forma más sencilla pero también podríamos haber utilizado otras. Retomemos la idea anterior de la intersección y pensemos un poco. Para que la gráfica corte al eje X la función tiene que valer cero, es decir También podríamos haberlo calculado utilizando la fórmula tradicional para la resolución de ecuaciones de segundo grado:
En nuestro ejemplo a = 1, b = 0 y c = 0. Sustituyendo en la ecuación y haciendo cada caso por su lado (positivo y negativo) tenemos:
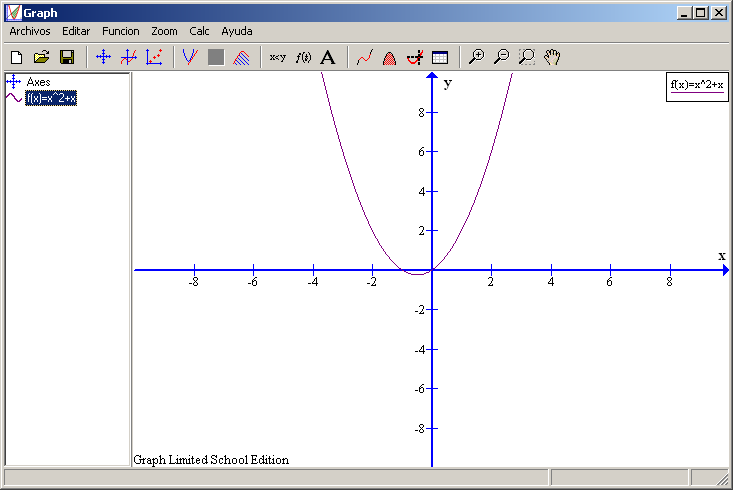
Tenemos dos casos (uno sumando 0 y otro restando 0) que dan el mismo resultado x = 0. Es decir la solución de la ecuación de segundo grado es lo que se llama una raíz doble, dos veces el mismo número. Luego, el punto de corte (que es un número real) de la función con el eje X es la solución a la ecuación de segundo grado. En nuestro caso cuando x = 0 y para dicho valor la función vale En resumidas cuentas podemos decir que: el punto de corte con el eje X coincide con el punto de corte con el eje Y y el valor mínimo de la función. Caso ax2+bx=0Pasemos al estudio de una función en la que ni a ni b son nulos y c = 0 (cuando ocurre esta última igualdad, se suele decir que el término independiente es cero). Para que no sea muy difícil en nuestro caso tanto a como b valdrán 1, por lo que la función tendrá esta forma Creemos una nuevo archivo y pulsemos en el botón Insertar una nueva función (el quinto por la izquierda de la barra de herramientas) para indicar la ecuación. Tras pulsar en OK la gráfica será así:
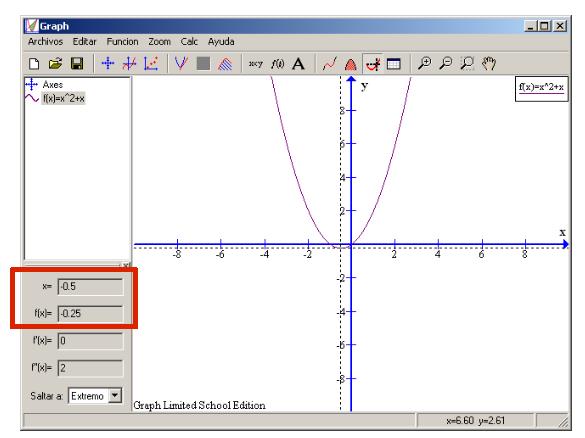
Observamos que es similar a la gráfica anterior: decrece conforme se acerca al eje Y y aumenta según se aleja de él. Como diferencias destacables vemos que corta al eje Y en sólo un punto, al eje X en dos y su mínimo es un punto que no coincide con ninguno de ellos. Calculemos las coordenadas de todos estos puntos. Teniendo seleccionado de la barra de herramientas el botón Evaluar la función seleccionada, elegimos del recuadro inferior izquierdo la opción Extremo. Aparece el punto (-0,5 , -0,25) como el lugar en que la función toma su mínimo.
Con respecto al punto de corte con el eje Y bastará con que elijamos del recuadro inferior izquierdo la opción Función (seguimos teniendo seleccionado el botón Evaluar la función seleccionada) y escribimos 0 en la primera casilla del recuadro inferior. Obtenemos que Por último veamos los puntos de corte con el eje X, o lo que es lo mismo las soluciones de la ecuación Elegimos esta vez la opción Eje-x de la casilla inferior. Pulsamos una vez a la izquierda del eje Y y obtenemos el punto (0 , 0). Si pulsamos a la derecha del eje Y sale como resultado el punto (-1 , 0). En este caso coincide el punto de corte con el eje Y con uno de los que intersecan al eje X.
En nuestro ejemplo a = 1, b = 1 y c = 0. Sustituyendo en la ecuación y haciendo cada caso por su lado (positivo y negativo) tenemos:
Por lo que las coordenadas de los puntos son (0 , 0) y (-1 , 0), tal y como averiguamos antes. Si conocemos las soluciones de una ecuación es posible escribir ésta en función de sus raíces. Si suponemos que una ecuación tiene por soluciones d y e, podemos escribir la ecuación como Escribimos la ecuación tal y como hemos indicado,
Si hacemos la multiplicación final tendremos,
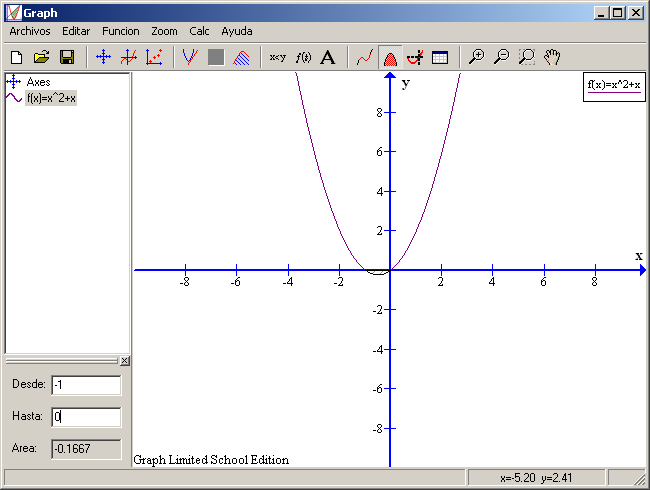
Podemos ver que es la ecuación original. Como punto final del estudio de este apartado y recordatorio de una de las herramienta que hemos visto antes calcularemos un área. Mirando la gráfica podemos observar que hay una región delimitada por el eje X y la función Marcamos la función de la columna de la izquierda y pulsamos en el botón Calcular el área debajo de un segmento de una curva (séptimo por la derecha de la barra de herramientas). Aparece en la parte inferior izquierda un recuadro, en cuya casilla Desde escribiremos -1 y en la de Hasta pondremos 0. Según el programa su área sería de -0,1667 unidades cuadradas. Como sabemos que todas las áreas son positivas, el valor correcto es 0,1667 unidades cuadradas.
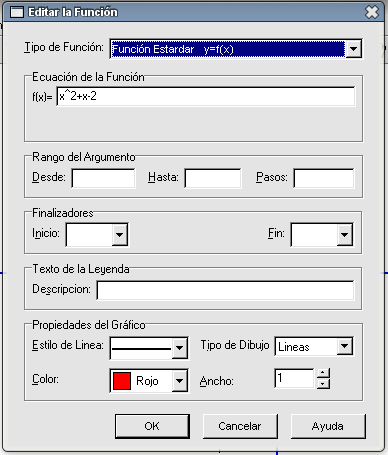
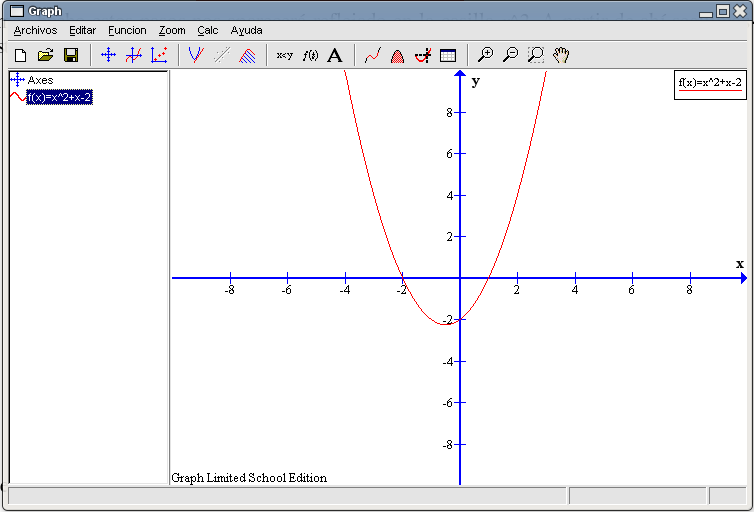
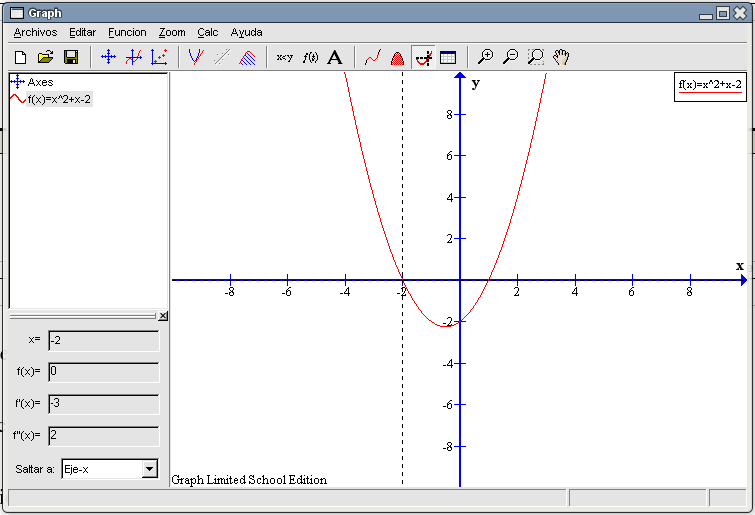
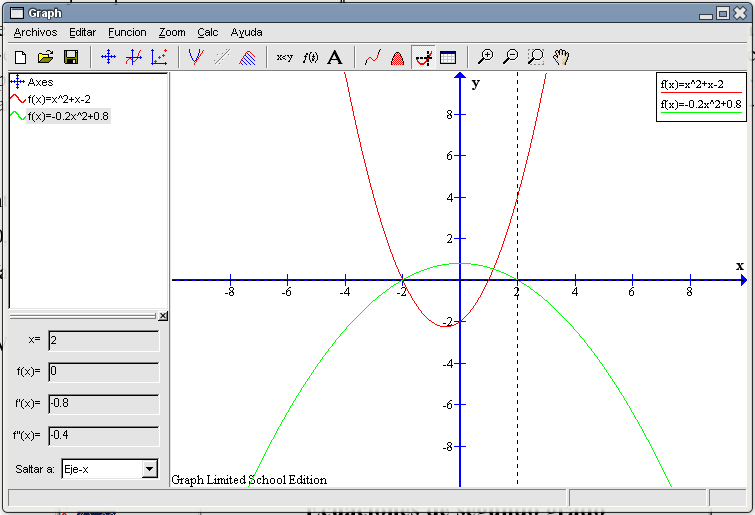
Caso ax2+bx+c=0Nuestra función de segundo grado será la siguiente: La ecuación asociada Como siempre, pulsamos en el botón Insertar ecuación y rellenamos la casilla Ecuación de la función con la ecuación. Tras pulsar en OK nos saldrá la siguiente gráfica:
Podemos observar en la gráfica que esta función siempre toma valores positivos (y a mayor número, mayor valor de la función) salvo para una pequeña parte que se encuentra en la zona negativa del eje Y. Esta zona está comprendida entre los puntos en que la gráfica corta al eje X. Averigüemos dichas intersecciones utilizando la herramienta que ya hemos visto en ejemplos anteriores. Seleccionamos de la barra de herramientas el botón Evaluar la función seleccionada y elegimos del recuadro inferior izquierdo la opción Eje-x. Con respecto al eje Y hay un punto a cada lado, si pulsamos en la parte izquierda nos aparecerá el valor -2 y si nos vamos al lado derecho nos dará como valor 1. Es decir, los puntos de corte con el eje X son (-2 , 0) y (1 , 0).
Estos dos valores (-2 y 1) también podríamos haberlos calculado utilizando la fórmula tradicional para la resolución de ecuaciones de segundo grado:
En nuestro ejemplo a = 1, b = 1 y c = -2. Sustituyendo en la ecuación y haciendo cada caso por su lado (positivo y negativo) tenemos:
Luego, los puntos de corte (que son números reales) de la función con el eje X son las soluciones a la ecuación de segundo grado. Como consecuencia, si una función no corta al eje X su ecuación no puede tener soluciones. Por tanto, también podemos escribir la ecuación asociada a la función de la siguiente forma:
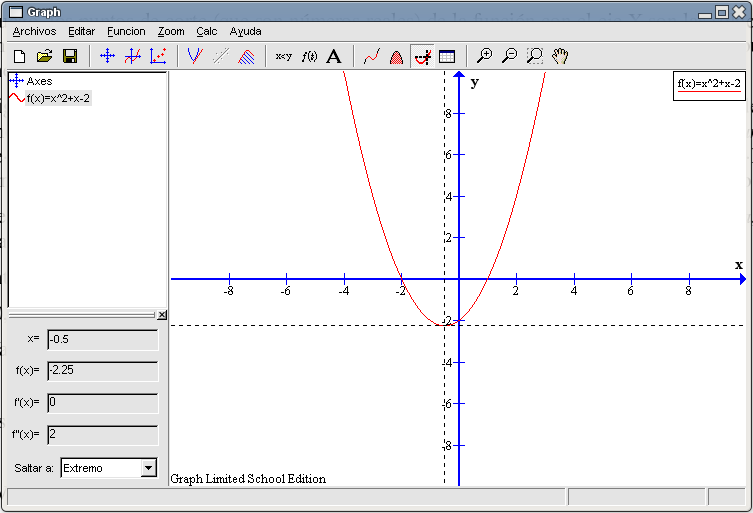
Sigamos estudiando la función y su trazado. La gráfica de esta función tiene un punto situado más bajo que ningún otro, es lo que se llama mínimo absoluto de la función. Vemos que cerca del eje Y la gráfica pasa de decrecer a crecer. Existe un número real cuyo valor en la función es el menor de todos los posibles. El programa nos permite calcular las coordenadas de dicho punto. Teniendo seleccionado de la barra de herramientas el botón Evaluar la función seleccionada, elegimos del recuadro inferior izquierdo la opción Extremo. Pulsamos en cualquier parte de la gráfica y obtenemos el punto (-0,5 , -2,25). El número real -0,5 es el que toma el mínimo valor en esta función, -2,25. Al igual que en casos anteriores calculemos el área de alguna región del plano. La más sencilla es la encerrada por la función entre los puntos de corte con el eje X. Seleccionamos de la barra de herramientas el botón Calcular el área debajo de un segmento de una curva. Como los cortes con el eje X son en -2 y 1, éstos serán los valores con los que rellenaremos las casillas del recuadro inferior izquierdo. El resultado que aparece es -4,5 unidades cuadradas y como ya sabemos de antes, el valor correcto es 4,5 unidades cuadradas.
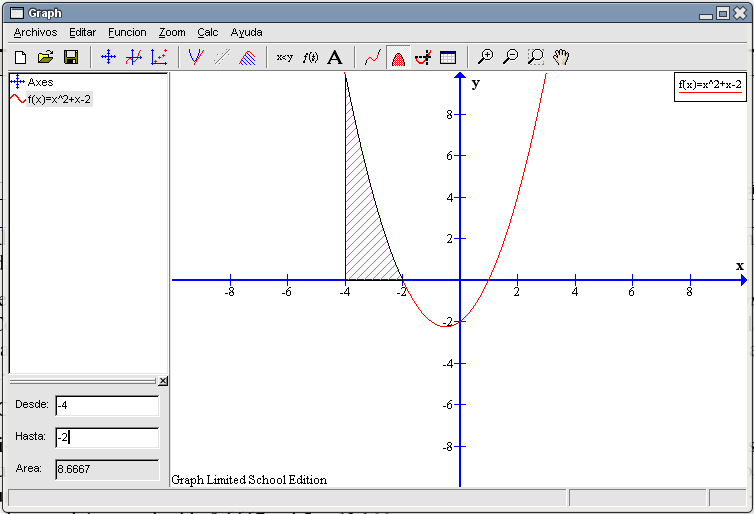
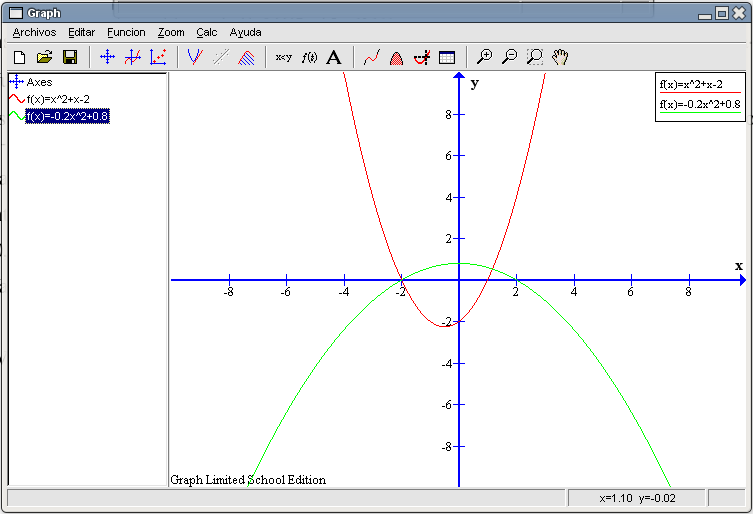
¿Cuánto vale el área definida por la función entre los valores -4 y 1? Si lo hacemos directamente el valor que obtendremos será , pero no es correcto puesto que estamos sumando un área positiva (entre -4 y -2) a un área negativa (entre -2 y 1). Deberemos calcular ambas áreas y luego sumarlas bien. El área entre -4 y -2 mide 8,6667 unidades cuadradas y la situada entre -2 y 1 vale 4,5 u.c., por lo que el área total mide: 8,6667 + 4,5 = 12,1667 unidades cuadradas Caso ax2+c=0Insertemos una nueva función de segundo grado en este archivo y trabajemos con ambas a la vez. Nuestra nueva función es la que tiene por ecuación: La ecuación asociada La gráfica asociada a esta función es la siguiente (en color limón):
Observamos que para valores grandes de x, tanto positivos como negativos, la función siempre vale números negativos muy grandes. Sólo cerca del eje Y la función toma valores positivos. Calculemos los puntos de corte con el eje X que nos definen dicha zona. Teniendo marcada en la zona izquierda de la ventana la función, seleccionamos de la barra de herramientas el botón Evaluar la función seleccionada y elegimos del recuadro inferior izquierdo la opción Eje-x. Con respecto al eje Y hay un punto a cada lado, si pulsamos en la parte izquierda nos aparecerá el valor -2 y si nos vamos al lado derecho nos dará como valor 2. Es decir, los puntos de corte son (-2 , 0) y (2 , 0). Como consecuencia de todo esto, las soluciones de la ecuación
Se nos ha olvidado incluir el coeficiente a que acompaña a
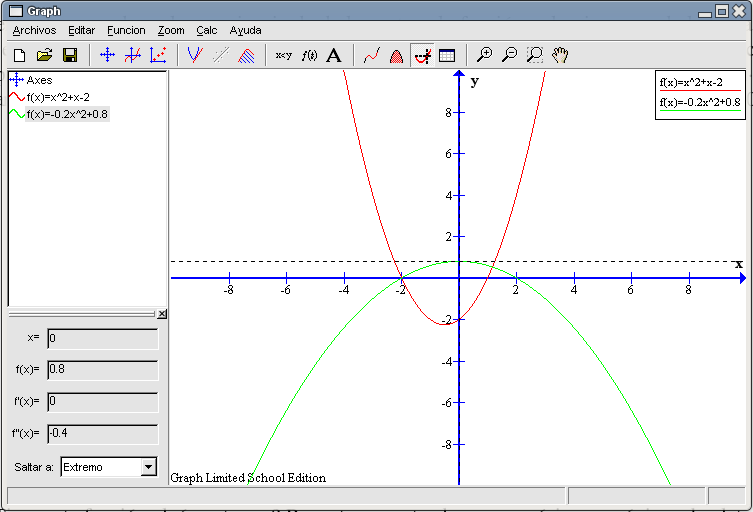
Ésto sí que es correcto. Por tanto la expresión buena es ¿Tiene este función algún extremo? Por extremo entendemos un mínimo o máximo absoluto. Mirando la gráfica, la única opción posible es la existencia de un máximo absoluto, un punto en el que la función llega a valer más que en ningún otro punto. Teniendo seleccionada la función y pulsado el botón Evaluar la función seleccionada, elegimos del recuadro inferior izquierdo la opción Extremo. Pulsamos en cualquier parte de la gráfica y obtenemos el punto (0 , 0,8). El número real 0 es el que toma el máximo valor en esta función (0,8).
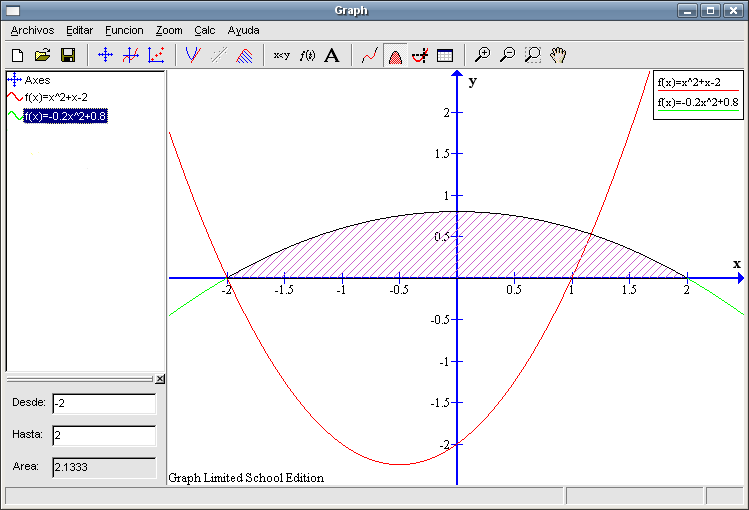
¿Cuánto vale el área encerrada entre los puntos de corte con el eje X? Seleccionamos de la barra de herramientas el botón Calcular el área debajo de un segmento de una curva. Como los cortes con el eje X son en -2 y 2, éstos serán los valores con los que rellenaremos las casillas del recuadro inferior izquierdo. El resultado que aparece es 2,1333 unidades cuadradas.
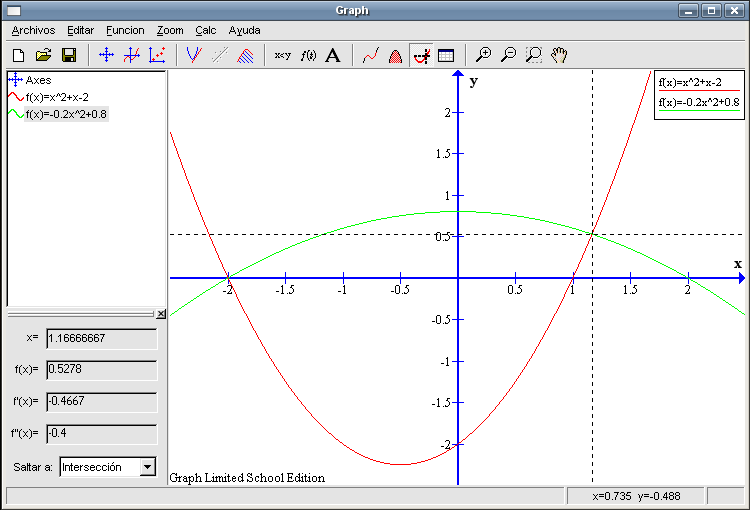
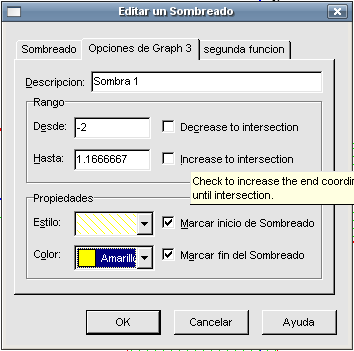
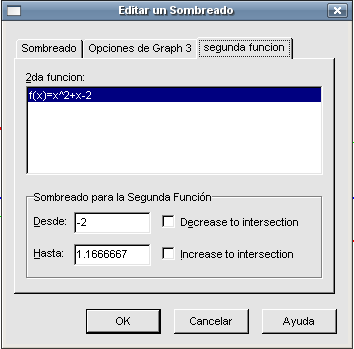
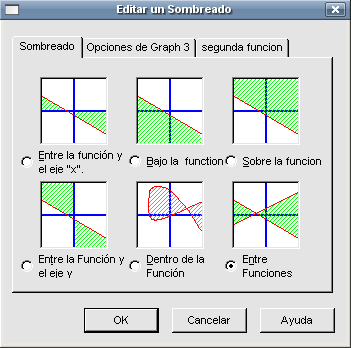
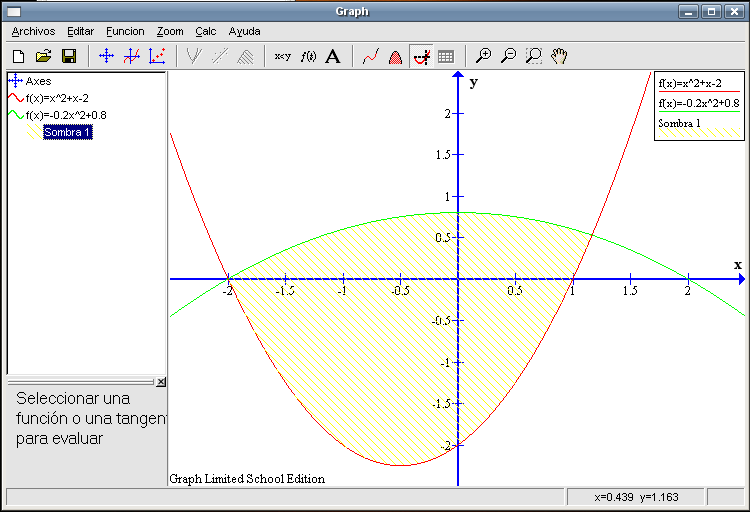
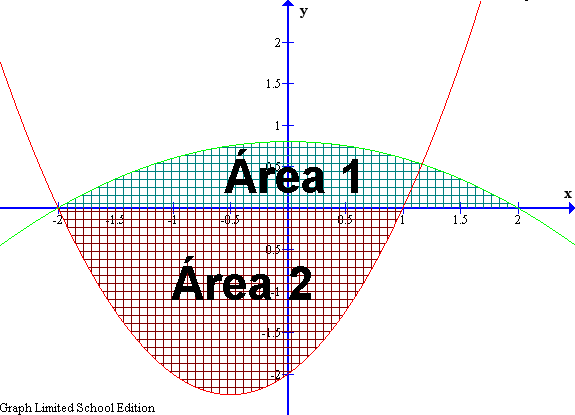
¿Podremos calcular el área encerrada entre las dos funciones que tenemos representadas? Directamente no es posible pero podemos descomponerla en varias partes y luego sumar lo que calculemos. Pero antes de avanzar. sería conveniente sombrear la zona en cuestión para poder visualizar mejor lo que deseamos calcular. Podemos ver que uno de los puntos en los que se cortan las dos gráficas es el (-2 , 0) y nos falta por averiguar cuál es el otro puesto que para sombrear es necesario saber dichos puntos. Teniendo seleccionada la función
Marcamos la función
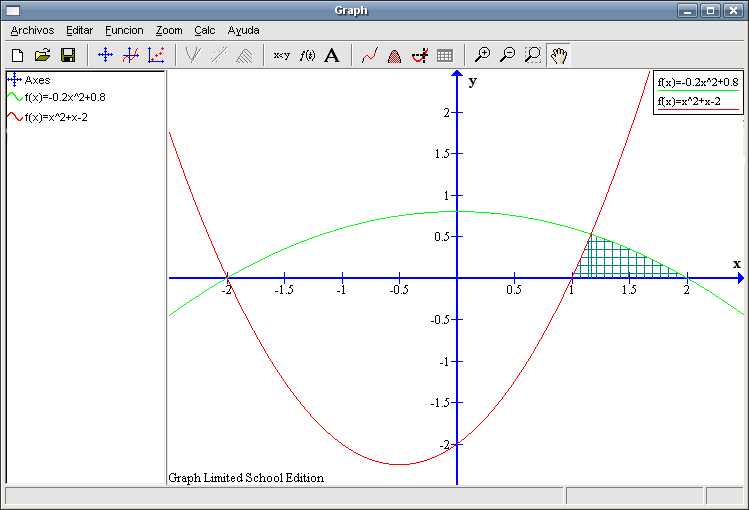
Ya sabemos la forma que tiene el área que deseamos calcular. Sigamos pensando y, aunque se puede calcular de otra forma, vamos a usar cosas que hemos hecho previamente para hallar la medida de la región. En pasos anteriores, hemos calculado un área para la función
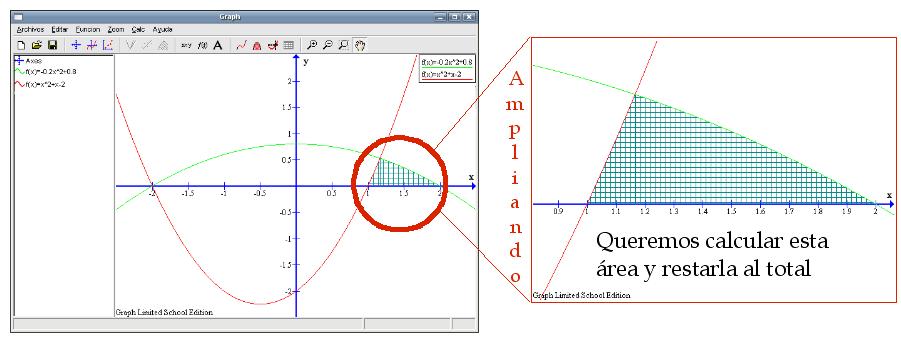
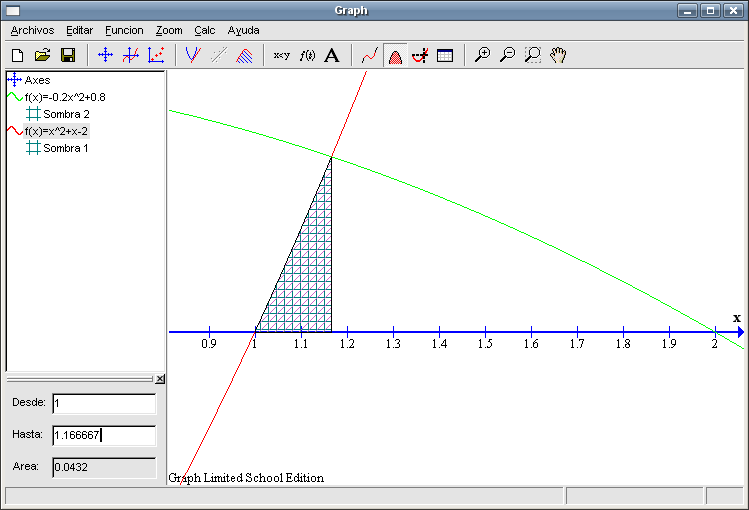
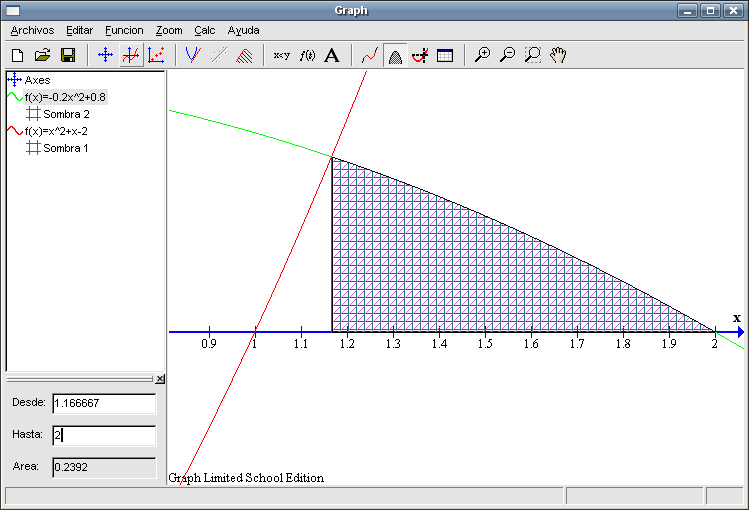
Si sumamos dichas áreas (recuadro a la derecha de la imagen anterior) tenemos más de lo que nos piden, hay una pequeña región a la derecha con forma de triángulo que nos sobra. Calcularemos la medida de esa zona y se la restaremos a la total que tenemos.
Cuando estudiamos las rectas vimos que podíamos descomponer áreas teniendo en cuenta las funciones que la delimitan. En este caso hay una primera parte, desde 1 a 1,166667, que la define la función
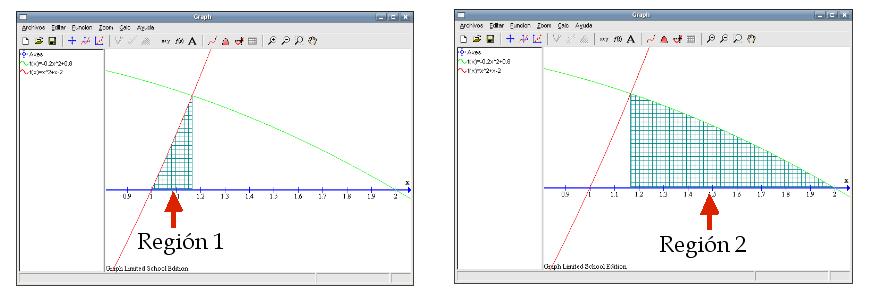
Para calcular la Región 1, seleccionamos de la columna izquierda la función
Hacemos lo mismo para calcular la Región 2: seleccionamos de la columna izquierda la función
Sumando obtenemos que el área de esta pequeña región con forma triangular es de: Área Región = Área Región 1 + Área Región 2 = 0,0432 + 0,2392 = 0,2824 unidades cuadradas Por tanto, y como punto final, el área que deseábamos calcular tendrá de extensión: Área final = Área total - Área Región = 6,6333 - 0,2824 = 6,3509 unidades cuadradas Ejercicio 3Realiza los siguientes ejercicios. Las tramas y colores los dejamos a tu elección. Guarda todos los ficheros en tu carpeta de trabajo con los nombres indicados entre paréntesis.
Como puedes observar las tres primeras parejas (1ª, 2ª y 3ª) son iguales en b y se diferencian en c; tal y como ocurre con las tres siguientes (4ª, 5ª y 6ª) y las tres últimas (7ª, 8ª y 9ª). También podemos verlo de otra manera: la 1ª, 4ª y 7ª son iguales en el término c y se diferencia en b; tal y como ocurre con las parejas 2ª, 5ª y 8ª y por otro lado con la 3ª, 6ª y 9ª. Recordemos que para poder visualizar sólo las funciones que interesen, hay que señalar en la barra de la izquierda cualquiera de las que deben quedar ocultas y pulsar el botón derecho del ratón. En el menú contextual que aparecerá tenemos que desmarcar la opción Visible.
Solución Ejercicio 3
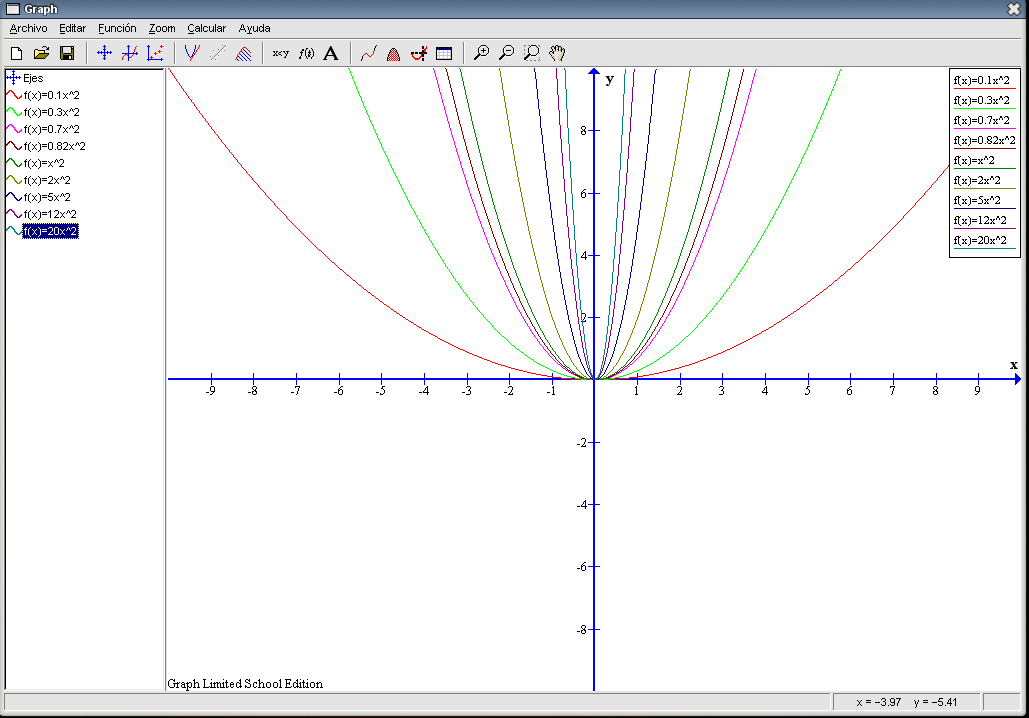 Cuanto más grande se hace a, más estrecha se hace la gráfica. Si vemos la gráfica como la forma de una U (u mayúscula), podemos decir que conforme se agranda a más fina se hace la U. Las nueve funciones cortan a los dos ejes en el mismo punto (0 , 0). Por tanto las soluciones de las ecuaciones asociadas son siempre la misma, en este caso 0, que es una raíz doble. Todas las gráficas quedan en el lado positivo del eje Y. También podemos observar que todas son simétricas con respecto a dicho eje; es decir, que la U queda divida exactamente por la mitad mediante el eje Y.
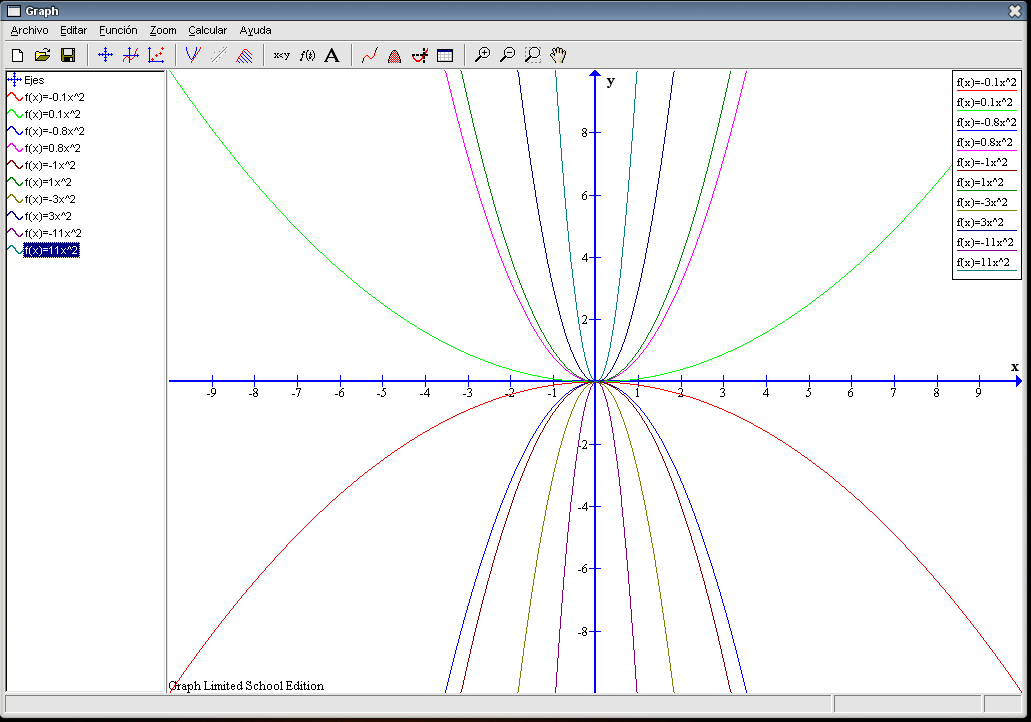 Si a toma un valor positivo la gráfica tiene forma de una U normal (estrechándose si a se hace más grande) y si toma valores negativos la gráfica tiene forma de una U invertida. Si a toma un valor positivo la gráfica queda en la parte positiva del eje Y; si toma un valor negativo la gráfica queda en la parte negativa del eje Y. En todos los casos las gráficas son simétricas con respecto al eje Y. Las diez funciones cortan a los dos ejes en el mismo punto (0 , 0). Por tanto, las soluciones de las ecuaciones asociadas son siempre la misma, en este caso 0, que es una raíz doble.
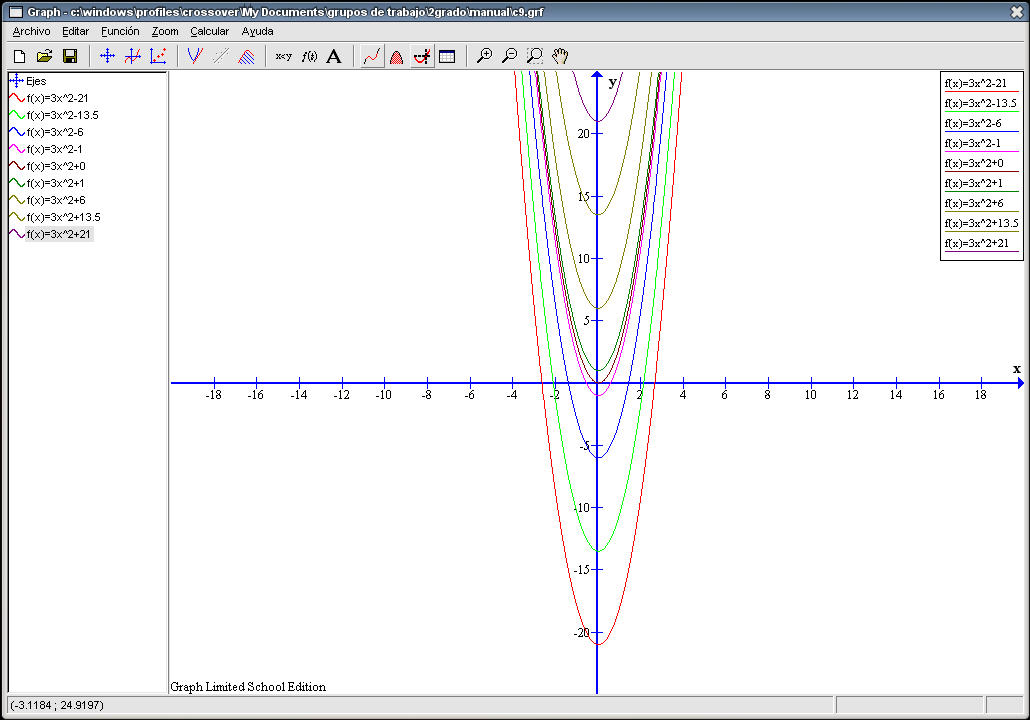 Conforme aumenta c la gráfica va subiendo por el eje Y. La U se desplaza por el eje Y cortándolo a la altura que indica el valor de c. Por ejemplo, si c = -6 la gráfica corta al eje Y en -6. Los puntos (sus coordenadas) de corte de cada una de ellas se indican en la siguiente tabla.
Podemos observar que los puntos de corte con el eje X son simétricos, uno a cada lado del eje Y a la misma distancia (uno negativo y el otro en positivo). Conforme aumenta c los puntos de corte pasan de dos a uno [la raíz doble (0 , 0)] y luego a ninguno. Las funciones cuya ecuación asociada tiene solución son sólo las que poseen puntos de corte con el eje X. En la siguiente tabla aparece la función, su ecuación asociada y las soluciones o raíces.
De la última ecuación podríamos decir que sólo tiene una solución, el cero. En verdad ,la última ecuación tiene lo que se dice una raíz doble. Ésto se debe a la ecuación
tiene una solución cuando consideramos el + del numerador y otra cuando tomamos el del numerador. En este caso por los dos caminos se llega al mismo resultado, cero. Mirando la gráfica global (con todos los gráficos) observamos que sólo las que tienen un valor positivo de c se quedan siempre en el lado positivo del eje Y. El resto siempre tienen una pequeña parte en la zona negativa del eje Y. También podemos observar que todas las gráficas son simétricas con respecto al eje Y, la U queda divida por la mitad por el eje Y.
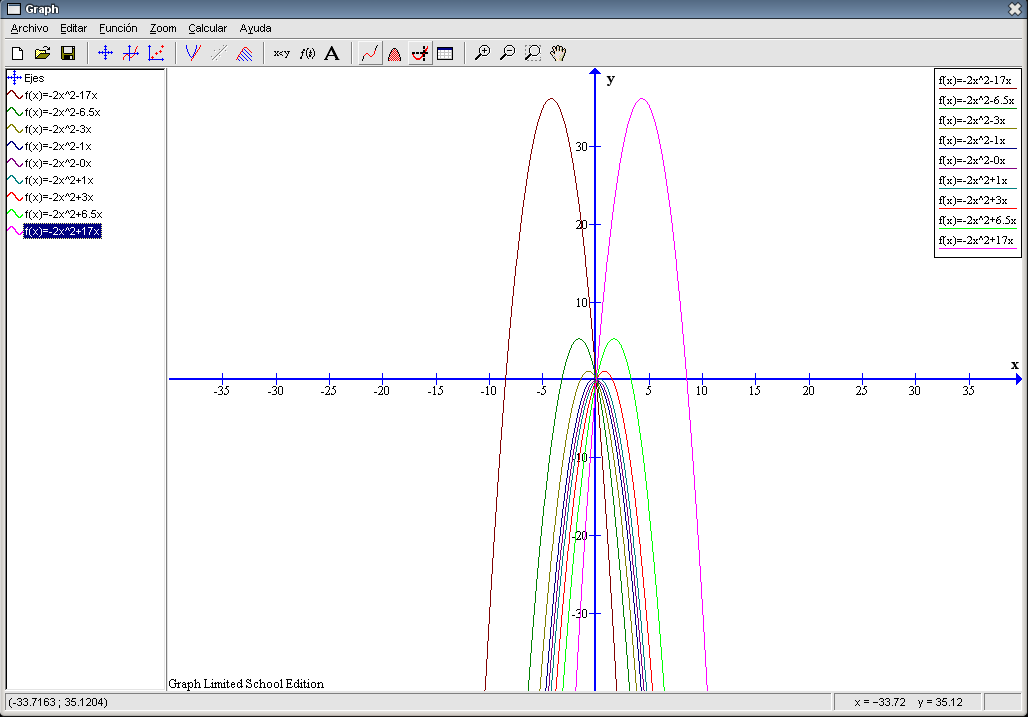
La imagen anterior nos permite contemplar todas las gráficas, pero la mayoría de ellas quedan muy juntas por lo que cuesta distinguirlas bien. En la siguiente captura aparece ampliada la zona en cuestión dejando las funciones 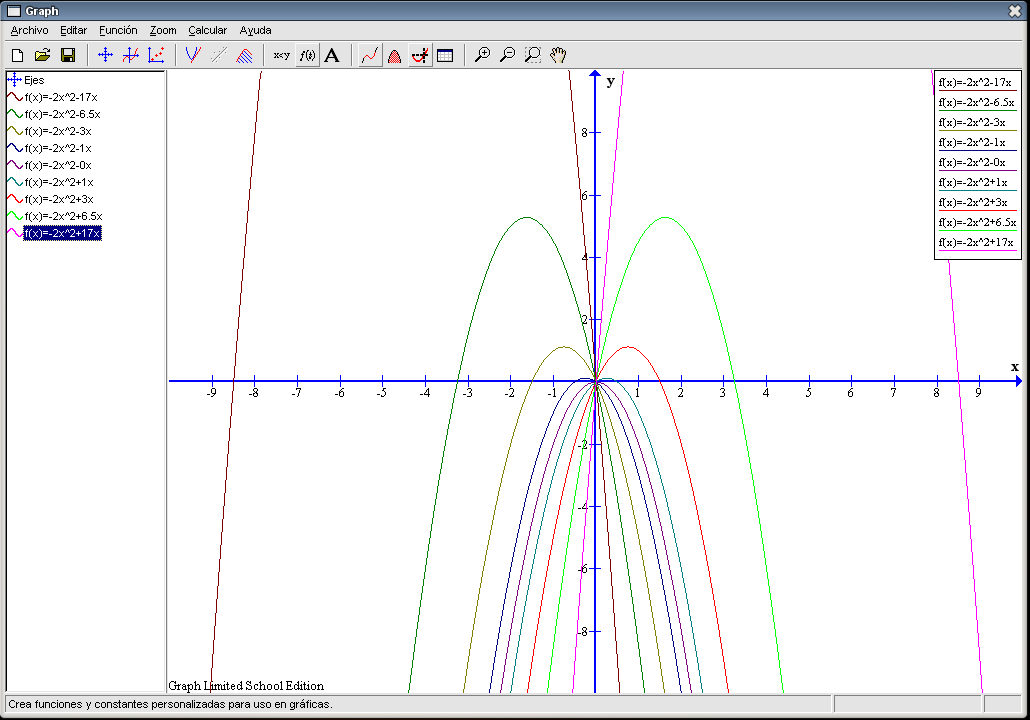
Todas las gráficas tienen forma de una U invertida. Empezamos con la gráfica Las gráficas son simétricas entre ellas con respecto al eje Y. Por ejemplo, la función Los puntos (sus coordenadas) de corte de cada una de ellas se indican en la siguiente tabla.
Podemos observar que los puntos de corte con el eje X son simétricos entre las funciones. El punto correspondiente a la función Tal y como ya vimos con la gráfica, todas pasan por el punto (0 , 0) que es a la vez el corte con el eje Y y con el eje X. En este caso todas las funciones tienen dos puntos distintos de corte con el eje X, salvo la función En la siguiente tabla aparece la función, su ecuación asociada y las soluciones o raíces.
Todas las gráficas tienen partes en las zonas positiva y negativa del eje Y, luego poco podemos decir sobre su situación. Sólo podemos comentar lo anteriormente dicho sobre la relación entre ellas, las gráficas son simétricas entre ellas con respecto al eje Y.
Si representamos las funciones y mostramos todas a la vez, sale un conjunto de trazos de los que no podemos decir mucho, salvo que todas las funciones tienen mínimos absolutos (forma de U). 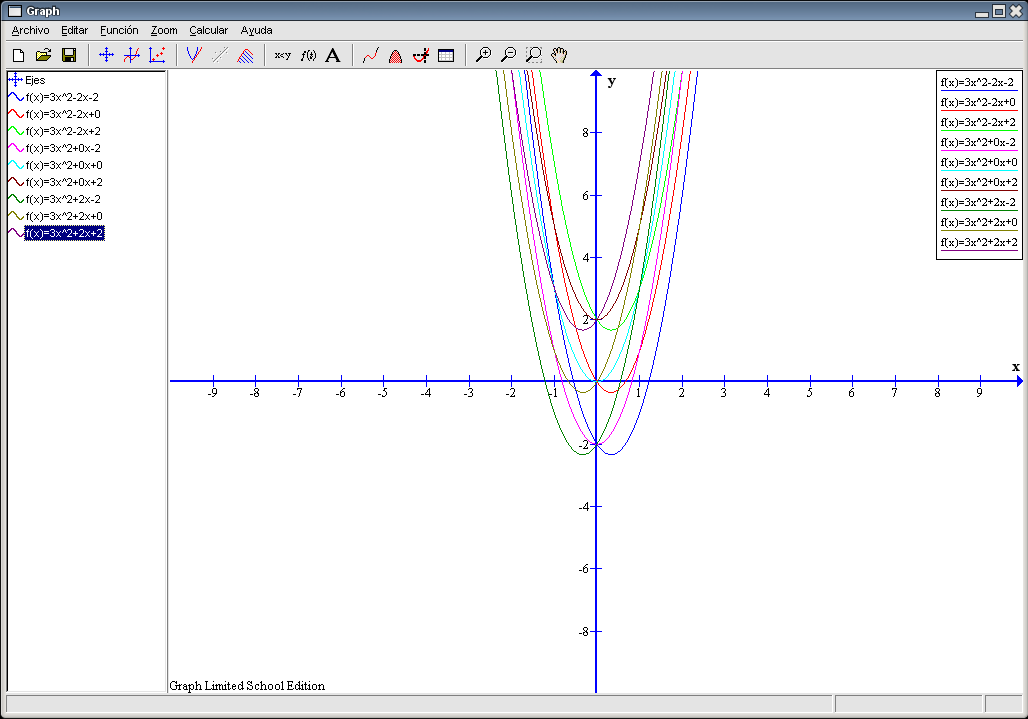
Empecemos con el primer apartado del ejercicio. Ocultamos todas las gráficas salvo las correspondientes a las parejas 1ª, 2ª y 3ª. El resultado es el siguiente: 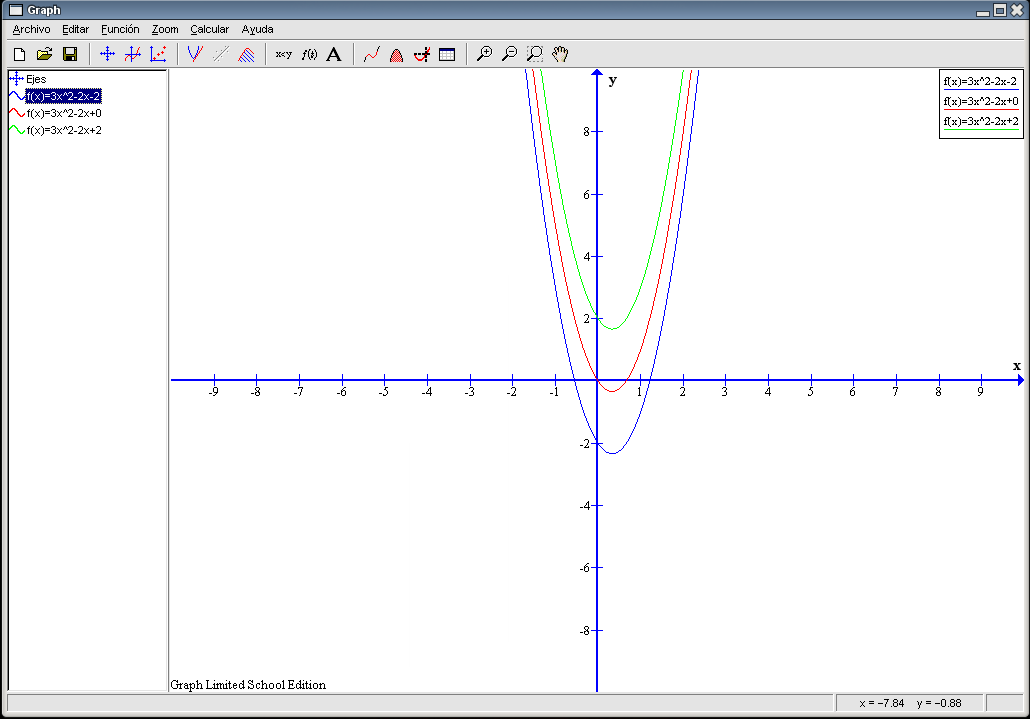
Las tres parejas se diferencian en el último término (c) siendo iguales a y b. Según varía c la U que describe la gráfica sube o baja su posición con respecto al eje Y. Vemos que la gráfica que corresponde a la 3ª pareja ( Observemos que ninguna de las gráficas es simétrica con respecto al eje Y, todas están desplazadas a la derecha de dicho eje. El eje Y no divide por la mitad a la U de la gráfica. Ocultamos estas tres gráficas y hacemos visibles correspondientes a las parejas 4ª, 5ª y 6ª. El resultado es esta imagen: 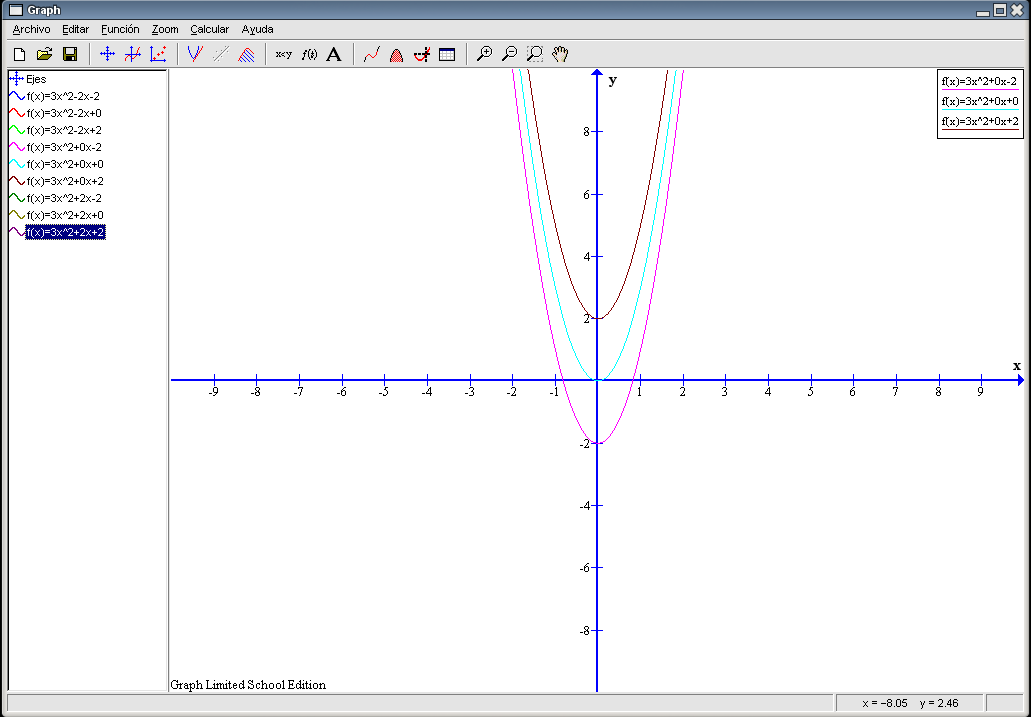
Al igual que antes las tres parejas se diferencian en el último término (c) siendo iguales a y b. Según varía c la U que describe la gráfica sube o baja su posición con respecto al eje Y. Vemos que la gráfica que corresponde a la 6ª pareja ( Observemos en este caso que todas las gráficas son simétricas con respecto al eje Y. El eje Y divide por la mitad a la U de la gráfica. Por último, ocultamos estas tres gráficas y hacemos visibles correspondientes a las parejas 7ª, 8ª y 9ª. El resultado es la siguiente imagen: 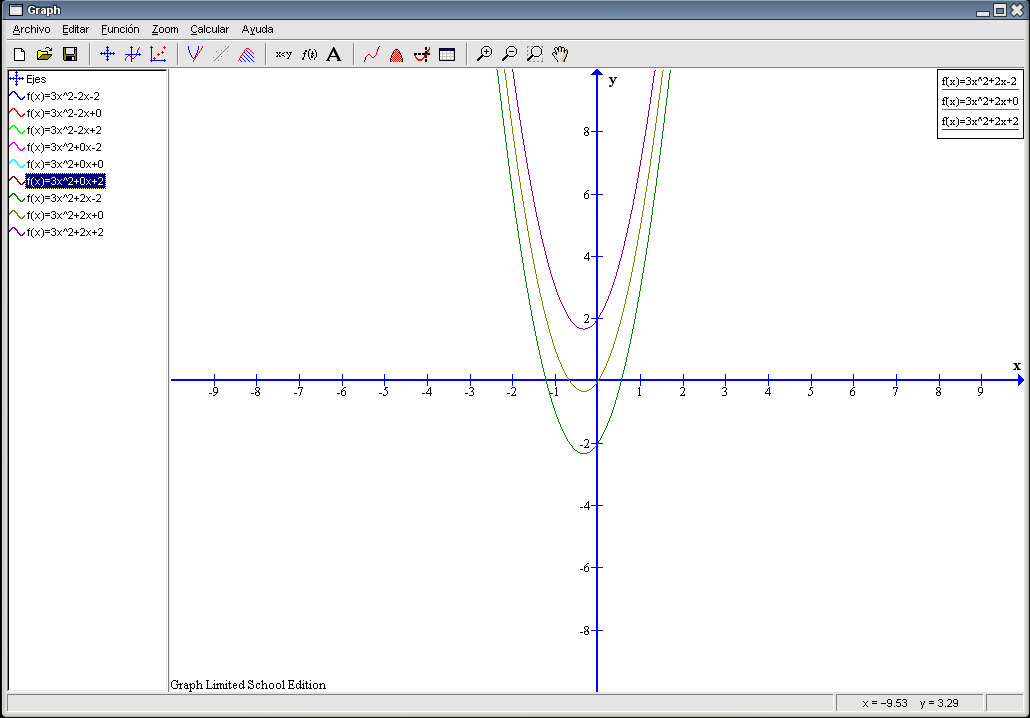
Tal y como antes, las tres parejas se diferencian en el último término (c) siendo iguales a y b. Según varía c la U que describe la gráfica sube o baja su posición con respecto al eje Y. Vemos que la gráfica que corresponde a la 9ª pareja ( Observemos que ninguna de las gráficas es simétrica con respecto al eje Y, todas están desplazadas a la izquierda de dicho eje. El eje Y no divide por la mitad a la U de la gráfica. Como conclusión de este apartado podemos decir que el término c hace que la gráfica suba o baje con respecto al eje Y. Pasemos al segundo apartado del ejercicio. Ocultamos todas las gráficas salvo las correspondientes a las parejas 1ª, 4ª y 7ª. El resultado es el siguiente: 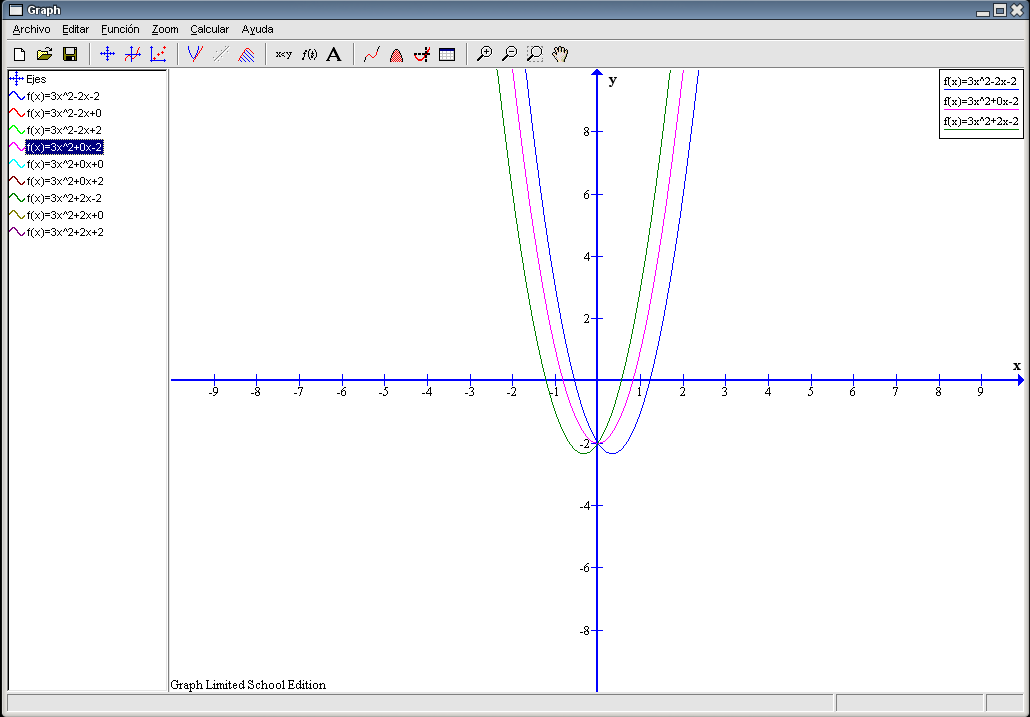
Las tres parejas se diferencian en el segundo término (b) siendo iguales a y c. Si b = 0 la gráfica es simétrica con respecto al eje Y, la U que se traza queda divida por la mitad por dicho eje. En los otros dos casos, la gráfica se desplaza hacia un lado u otro con respecto a dicho eje: si b es positivo hacia la izquierda y si b es negativo hacia la derecha. También podemos decir que las gráficas se desplazan hacia abajo en estas parejas. Observemos que todas cortan al eje X en dos puntos diferentes, quedando cada uno a un lado del eje Y. Ocultamos estas tres gráficas y hacemos visibles correspondientes a las parejas 2ª, 5ª y 8ª. El resultado es esta imagen: 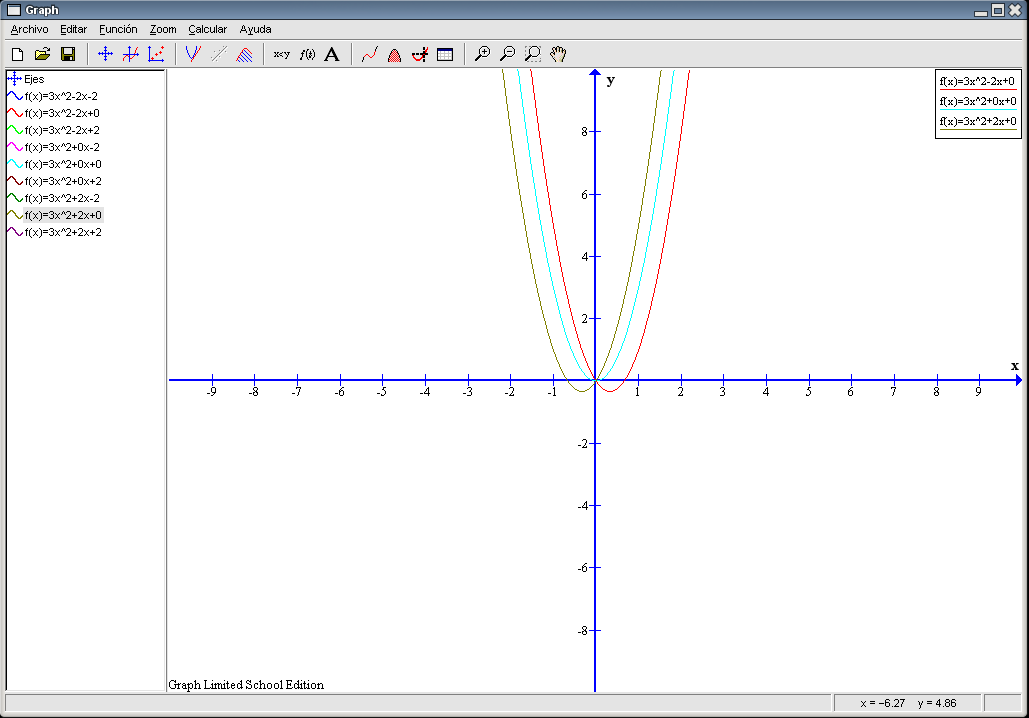
Las tres parejas se diferencian en el segundo término (b) siendo iguales a y c. Si b = 0 la gráfica es simétrica con respecto al eje Y, la U que se traza queda divida por la mitad por dicho eje. En los otros dos casos, la gráfica se desplaza hacia un lado u otro con respecto a dicho eje: si b es positivo hacia la izquierda y si b es negativo hacia la derecha. También podemos decir que las gráficas se desplazan hacia abajo en estas parejas. Observemos que la gráfica de Por último, ocultamos estas tres gráficas y hacemos visibles correspondientes a las parejas 3ª, 6ª y 9ª. El resultado es la siguiente imagen: 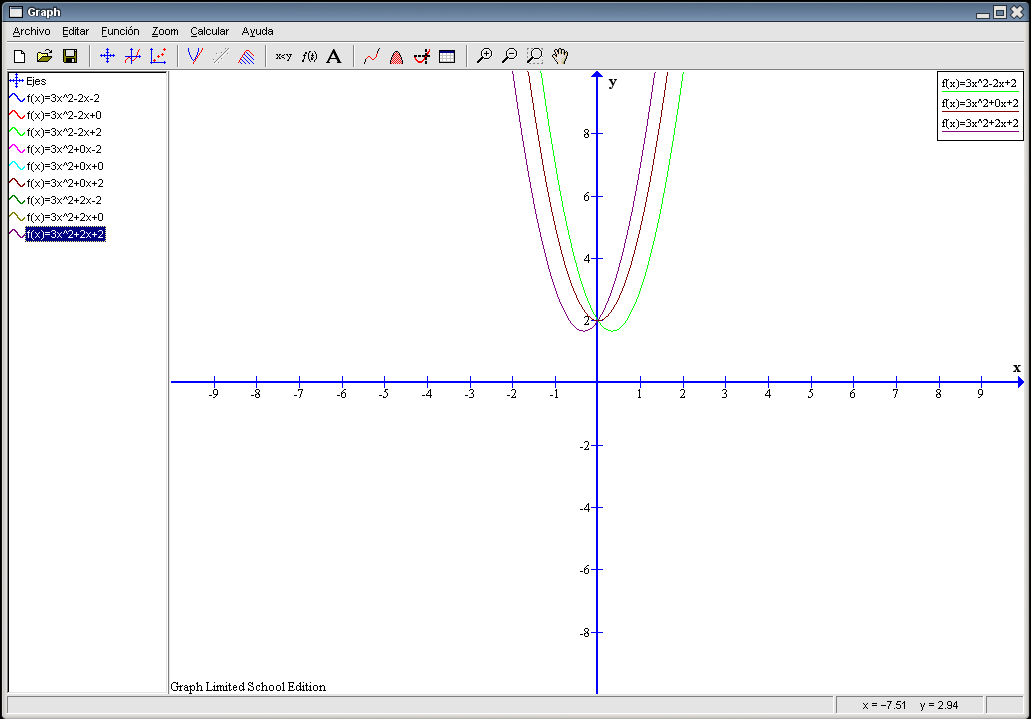
Las tres parejas se diferencian en el segundo término (b) siendo iguales a y c. Si b = 0 la gráfica es simétrica con respecto al eje Y, la U que se traza queda divida por la mitad por dicho eje. En los otros dos casos, la gráfica se desplaza hacia un lado u otro con respecto a dicho eje: si b es positivo hacia la izquierda y si b es negativo hacia la derecha. También podemos decir que las gráficas se desplazan hacia abajo en estas parejas. Observemos que ninguna de las gráficas corta al eje X. Como conclusión de este apartado podemos decir que el término b hace que la gráfica se desplace hacia la izquierda o la derecha con respecto al eje Y. En todos los casos la gráfica se desplaza hacia abajo. Realicemos el tercer apartado del ejercicio. Recordemos un par de cosas:
Siguiendo lo expuesto tenemos en resumen que las coordenadas aproximadas de los puntos de corte son (hemos redondeado en la cuarta cifra decimal por razones de comodidad a la hora de trabajar):
Observemos la repetición que hay en la serie de puntos de corte con el eje Y fruto de variar c entre -2, 0 y 2. Las parejas 4ª, 5ª y 6ª tienen raíces simétricas (son los mismos valores pero cambiados de signo) con respecto al 0 (origen del eje X). Recordemos que sus gráficas eran simétricas con respecto al eje Y. Las parejas 1ª y 7ª tienen las mismas raíces pero cambiadas de signo, al igual que las parejas 2ª y 8ª. Esta relación entre las raíces es consecuencia de la variación de b entre -2, 0 y 2. Para finalizar este ejercicio hagamos el cuarto apartado. Recordemos que para que la ecuación asociada a una función de segundo grado tenga alguna solución, la gráfica debe cortar al eje X. Por tanto las soluciones de las ecuaciones asociadas a estas funciones son (hemos redondeado en la cuarta cifra decimal por razones de comodidad a la hora de trabajar):
Los comentarios que se pueden hacer sobre las relaciones entre las diferentes soluciones son los mismos que se realizaron en el apartado anterior.
Representando la función obtenemos la siguiente gráfica: 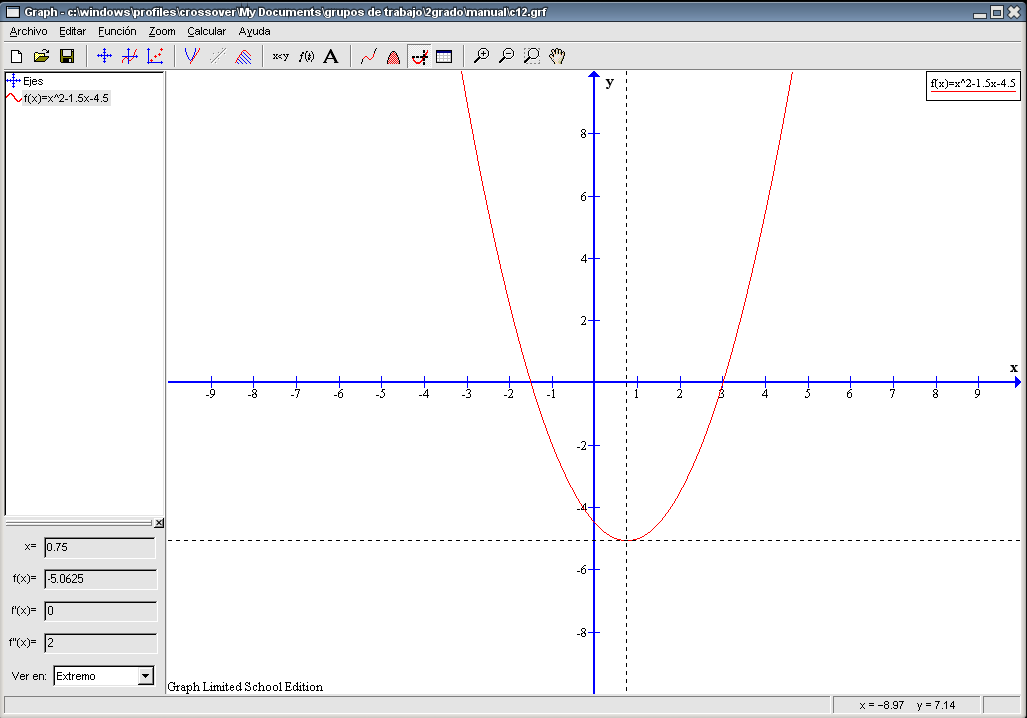
Para calcular el punto de corte con el eje Y, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Función. Escribimos en la primera casilla 0 y obtenemos como resultado en el siguiente recuadro -4,5. Luego las coordenadas del punto de corte con el eje Y son (0 , -4,5). Para calcular los puntos de corte con el eje X, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Eje-x. Pulsamos en cualquier parte de la zona situada a la izquierda del eje Y, obteniendo el punto (-1,5 , 0). Si pulsamos en cualquier lugar de la región situada a la derecha del eje Y, conseguimos el punto (3 , 0). Éstas son las coordenadas de los dos puntos pedidos. Dado que la función Para calcular el extremo seleccionamos la función, pulsamos el botón Evaluar la función seleccionada, elegimos del recuadro inferior izquierdo la opción Extremo. Pulsamos en cualquier parte de la gráfica y obtenemos el punto (0,75 , -5,0625). En este caso y viendo la gráfica podemos decir que este extremo es un mínimo. 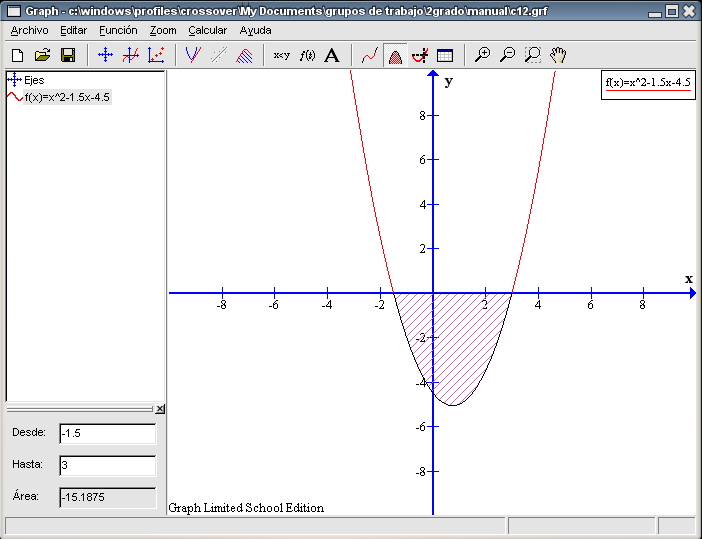
Para calcular el área que nos piden hacemos lo siguiente: seleccionamos de la columna izquierda la función
Representamos la función y obtenemos la siguiente gráfica: 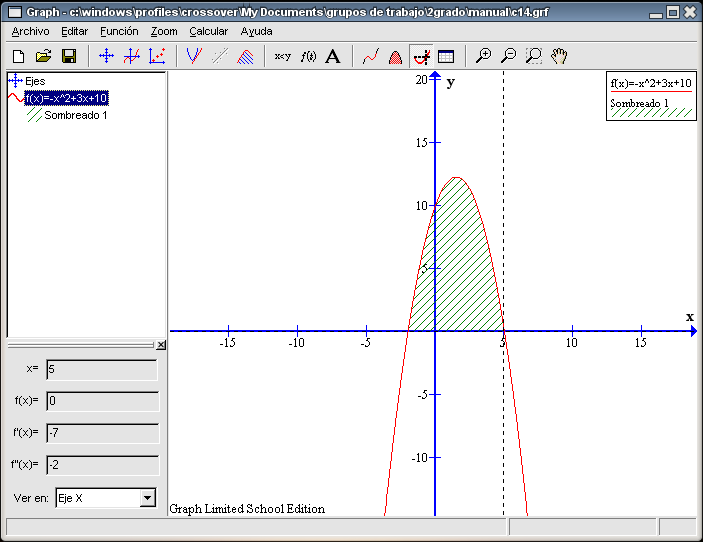
Para calcular el punto de corte con el eje Y, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Función. Escribimos en la primera casilla 0 y obtenemos como resultado en el siguiente recuadro 10. Luego las coordenadas del punto de corte con el eje Y son (0 , 10). Para calcular los puntos de corte con el eje X, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Eje-x. Pulsamos en cualquier parte de la zona situada a la izquierda del eje Y, obteniendo el punto (-2 , 0). Si pulsamos en cualquier lugar de la región situada a la derecha del eje Y, conseguimos el punto (5 , 0). Éstas son las coordenadas de los dos puntos pedidos. Dado que la función Para calcular el extremo seleccionamos la función, pulsamos el botón Evaluar la función seleccionada, elegimos del recuadro inferior izquierdo la opción Extremo. Pulsamos en cualquier parte de la gráfica y obtenemos el punto (1,5 , 12,25). En este caso y viendo la gráfica podemos decir que este extremo es un máximo. Marcamos la función Para calcular el área que nos piden hacemos lo siguiente: seleccionamos de la columna izquierda la función
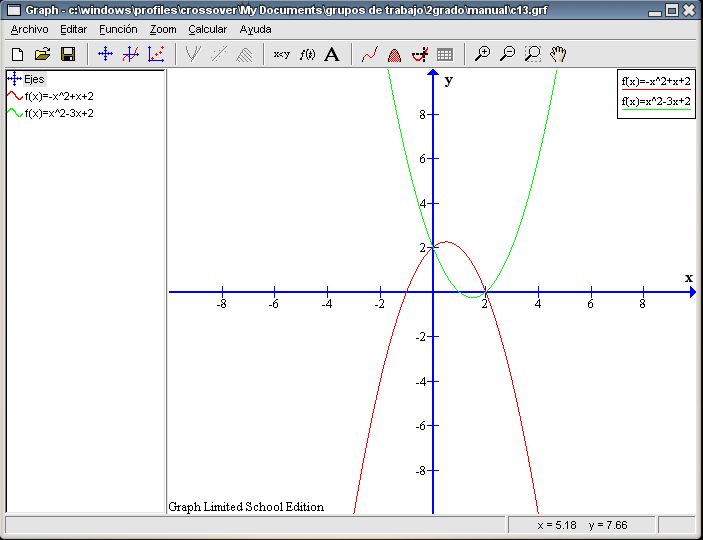
Representamos las dos funciones obteniendo las siguiente gráficas:
Estudiemos primero los puntos de corte de la función Para calcular el punto de corte con el eje Y, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Función. Escribimos en la primera casilla 0 y obtenemos como resultado en el siguiente recuadro un 2. Luego las coordenadas del punto de corte con el eje Y son (0 , 2). Para calcular los puntos de corte con el eje X, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Eje-x. Pulsamos en cualquier parte de la zona situada a la izquierda del eje Y, obteniendo el punto (-1 , 0). Si pulsamos en cualquier lugar de la región situada a la derecha del eje Y, conseguimos el punto (2 , 0). Éstas son las coordenadas de los dos puntos pedidos. Dado que la función ¿Es correcta esta forma de escribir la ecuación? Hagamos los productos indicados y simplifiquemos.
Lo que obtenemos es la ecuación
Éste sí es correcto, concuerda con la ecuación original. Nos queda por averiguar los puntos de corte para la función Para calcular el punto de corte con el eje Y, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Función. Escribimos en la primera casilla 0 y obtenemos como resultado en el siguiente recuadro el número 2. Luego las coordenadas del punto de corte con el eje Y son (0 , 2). En este caso coincide con el punto de corte de la otra función estudiada. Para calcular los puntos de corte con el eje X, seleccionamos el botón Evaluar la función seleccionada y elijamos del recuadro inferior izquierdo la opción Eje-x. Pulsamos en cualquier parte de la zona situada a la izquierda del eje Y, obteniendo el punto (1 , 0). Si pulsamos en cualquier lugar de la región situada a la derecha del eje Y, conseguimos el punto (2 , 0). Éstas son las coordenadas de los dos puntos pedidos. Dado que la función Por si no estamos seguros de esta respuesta, hagamos los productos indicados y simplifiquemos:
El resultado final del desarrollo concuerda con la ecuación original, luego está bien escrita la ecuación Sigamos el estudio de las funciones con el cálculo de sus extremos. Empezaremos con la función Hacemos lo mismo pero con la función Contestados los dos primeros apartados del ejercicio hagamos el tercer punto: calcular el área encerrada por la función Para calcular el área que nos piden hacemos lo siguiente: seleccionamos de la columna izquierda la función 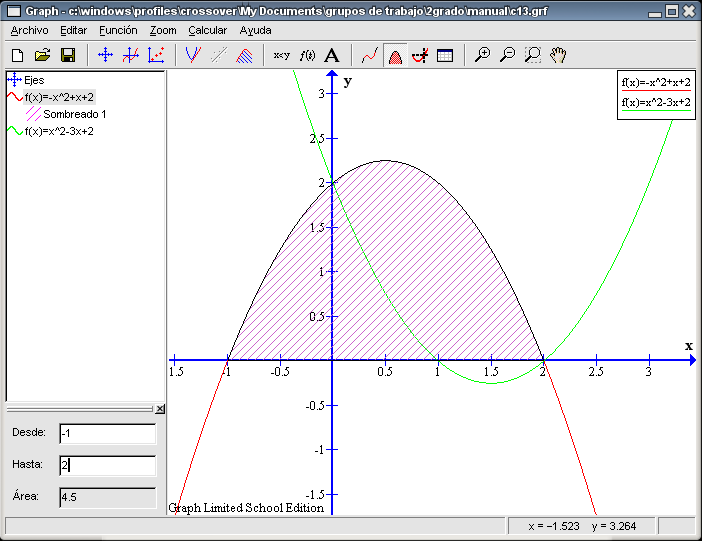
Realicemos el cuarto apartado, calcular el área encerrada por la función Para calcular el área que nos piden hacemos lo siguiente: seleccionamos de la columna izquierda la función 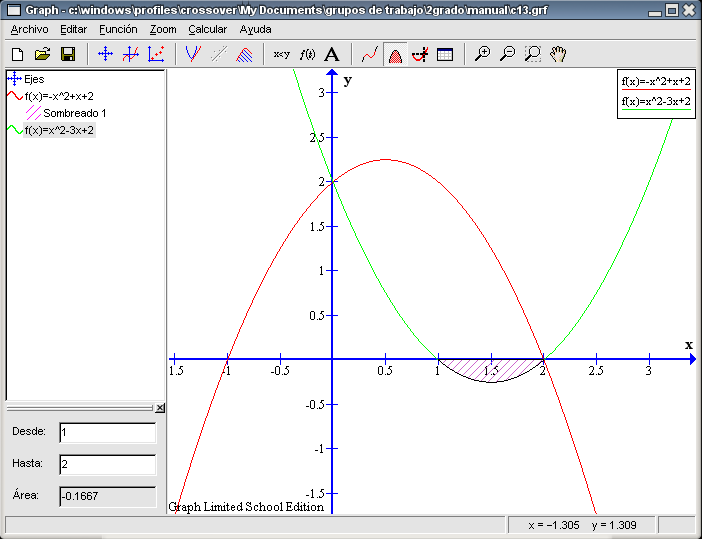
Nos queda por resolver el último apartado del problema: sombrear y calcular el área encerrada entre las intersecciones de las dos funciones. Recordemos que la herramienta Evaluar la función seleccionada nos permite calcular las coordenadas de la intersección de las funciones mediante la opción Intersección. Teniendo señalada cualquiera de las dos funciones (de la columna de la izquierda), elegimos Intersección del menú desplegable del recuadro inferior izquierdo. Pulsamos en cualquier parte a la izquierda del eje Y, en el recuadro aparecerá en la primera casilla un 0 y en la segunda un 2; por tanto el punto (0 , 2) es uno de los puntos de intersección. Ahora pinchamos en cualquier parte a la derecha del eje Y, en el recuadro aparecerá en la primera casilla un 2 y en la segunda un 0; por tanto el punto (2 , 0) es el otro punto de intersección. 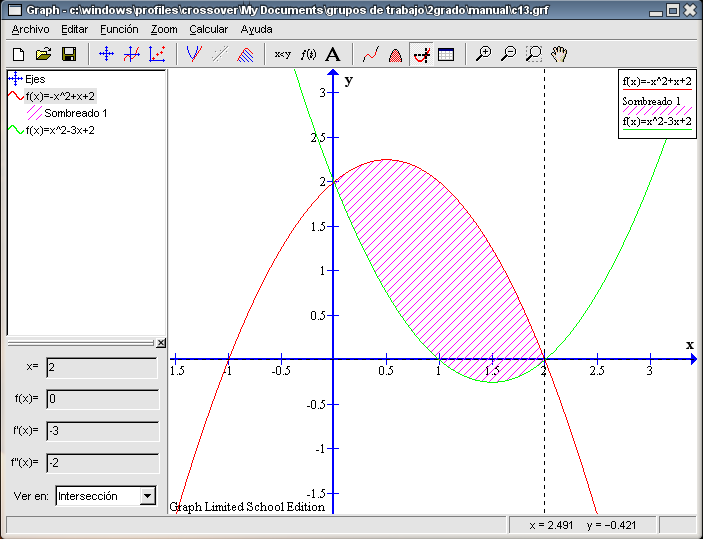 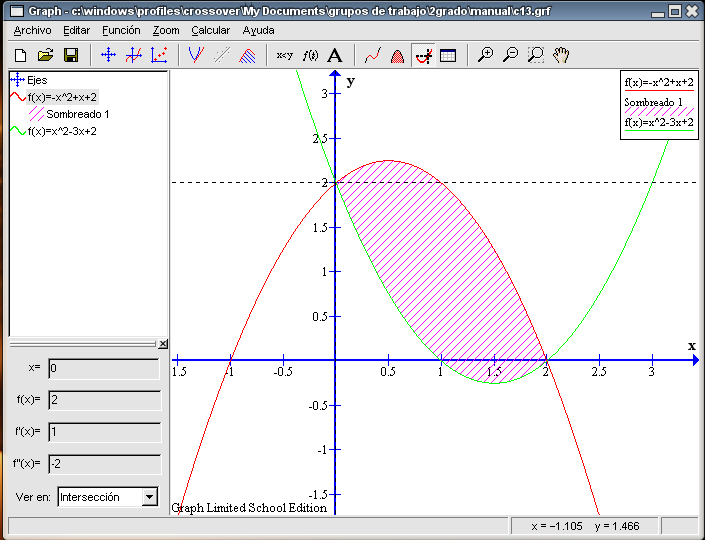
Hemos calculado los dos puntos de intersección que nos van a servir en primer lugar para sombrear la zona cuya área nos piden averiguar. Marcamos la función
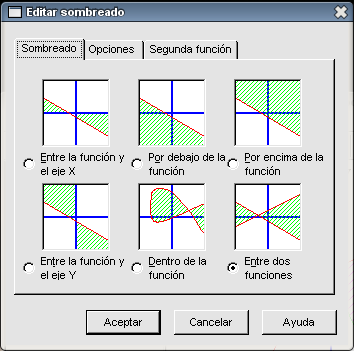 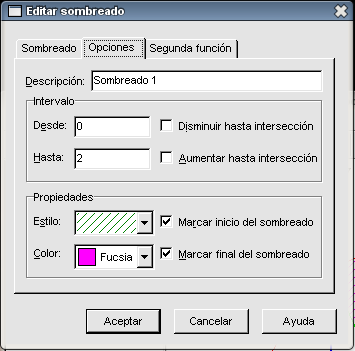 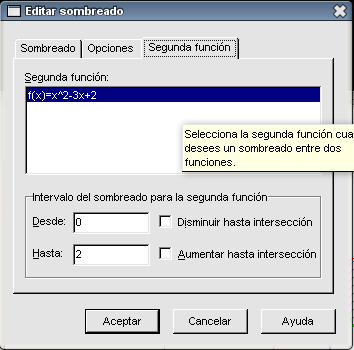
El resultado es el siguiente: 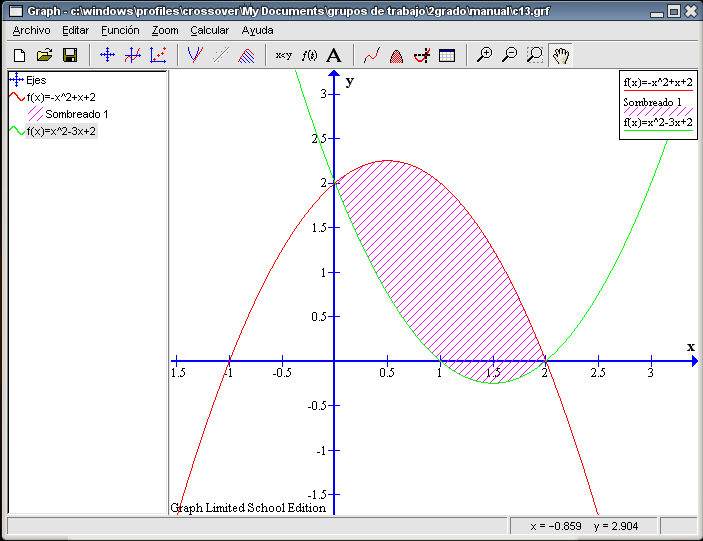
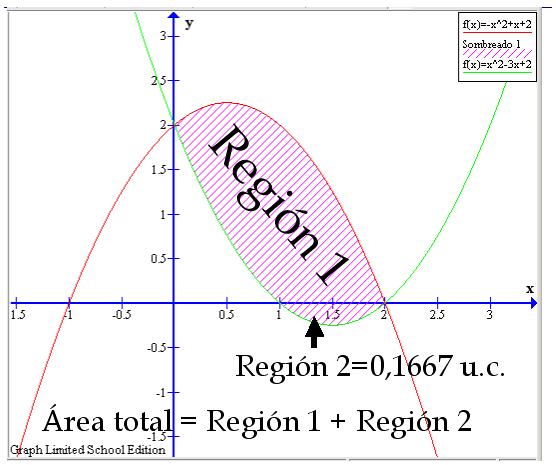
No es posible calcular directamente el área que nos piden, por lo que habrá que pensar un poco y dividir la región en partes que sí podamos trabajarlas con el programa. Vamos a seguir la misma técnica que vimos cuando trabajamos en la última parte dedicada a las ecuaciones de segundo grado. De toda la zona que nos piden averiguar, sabemos lo que vale el área una pequeña región que se encuentra por debajo del eje X de coordenadas. La hemos calculado en el apartado anterior y vale 0,1667 unidades cuadradas. En la siguiente imagen hemos llamado Región 2 a esta parte y al resto la hemos nombrado como Región 1. Nos falta por encontrar lo que vale esta región.
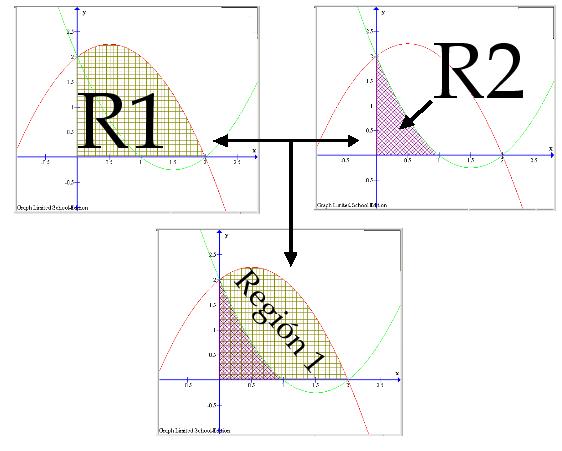
La Región 1 es posible verla como la diferencia entre otras dos zonas y que podemos calcular fácilmente con el programa. Observando las dos siguientes imágenes podemos deducir que el valor de la Región 1 es quitarle a la zona llamada R1 la parte correspondiente a R2. Estas dos (R1 y R2) son calculables utilizando el programa y las funciones que hemos trazado.
Pasemos a calcular las áreas de R1 y R2. La región R1 está definida por la función 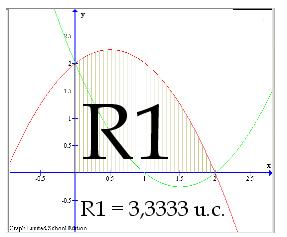
Para calcular el área que nos piden hacemos lo siguiente: seleccionamos de la columna izquierda la función Averigüemos el valor de la región R2. Esta región R2 está definida por la función Para calcular el área que nos piden hacemos lo siguiente: seleccionamos de la columna izquierda la función 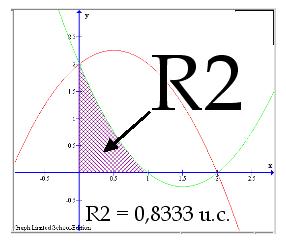 Por tanto el valor de la Región 1 es: Por tanto el valor de la Región 1 es:Región 1 = R1 R2 = 3,3333 0,8333 = 2,5 unidades cuadradas Como conclusión el valor del Área total que nos pedían es:
Área total = Región 1 + Región 2 = 2,5 + 0,1667 = 2,6667 unidades cuadradas
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||