| Graph II |
 |
 |
 |
| SOFTWARE - Software educativo |
| dimarts, 20 de maig de 2008 22:54 |
|
There are no translations available. Descubre a través de este tutorial esta sencilla herramienta para dibujar gráficas... Tutorial Graph II (Creación de gráficas)5. Primeros pasosLa primera vez que abramos el programa, nos aparecerá una pequeña ventana con la sugerencia del día, una indicación para trabajar con el programa. Si no queremos que aparezca esta ventana cada vez que iniciemos el programa, habrá que desmarcar la casilla que aparece en la parte inferior de dicho recuadro.
Cuando arranque el programa nos aparecerá una ventana similar la siguiente: 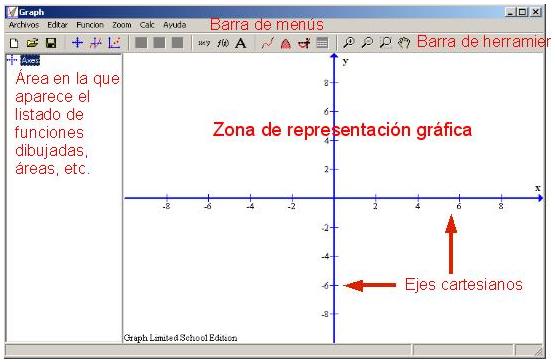
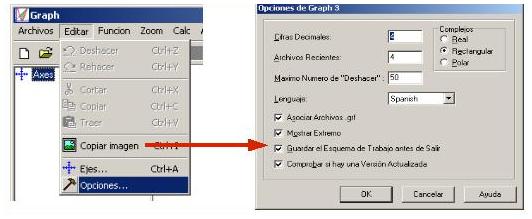
Si deseamos configurar el programa (por ejemplo cambiar el idioma de trabajo) tendremos que irnos a Editar Opciones (en inglés Edit Options).
La mayoría de los valores que aparecen por defecto son válidos para el trabajo diario por lo que no será necesario cambiar nada de la ventana. Ojo, la opción Mostrar Extremo no está relacionada con los posibles extremos de una función. Es una mala traducción y en verdad lo que nos permite es elegir si queremos que, al situar el cursor sobre algún objeto nos muestre una pequeña indicación de para qué sirve. 5.1. Barra de menúsLa barra de menús del programa nos sirve para acceder a todas las funciones que posee. En nuestro caso consta de seis opciones: Archivos, Editar, Función, Zoom, Calc y Ayuda.
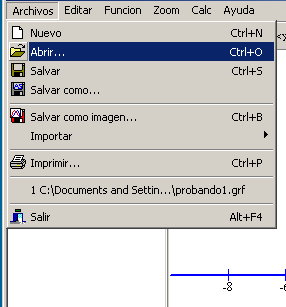
El submenú Archivos nos permite trabajar con los ficheros que generamos con el programa: crear uno nuevo; abrirlos; guardarlos o salvarlos con otro nombre; exportar la gráfica (salvar como imagen de mapa de bits o metafile); importar una serie de datos o un gráfico creado previamente; imprimir; abrir algún documento reciente y salir del programa.
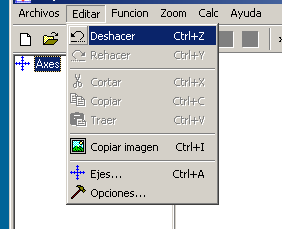
El submenú Editar nos permite: deshacer o rehacer alguno de los pasos que hemos hecho en nuestro trabajo; cortar, copiar y pegar lo seleccionado; Copiar la imagen (la gráfica) en el portapapeles (para luego por ejemplo pegarla en nuestro procesador de texto); modificar los ejes de la gráfica (Ejes) y las opciones generales del programa (Opciones).
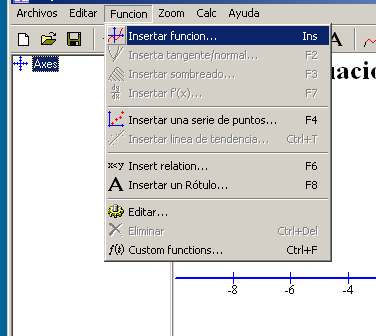
El submenú Función nos permite: crear una función para su representación gráfica, insertar la tangente en un punto de la gráfica, sombrear alguna parte del gráfico, dibujar una serie de puntos (datos), insertar una función que describa una serie de puntos, insertar una relación entre las variables o un rótulo, editar o borrar una función creada, o generar funciones propias (diferentes de las que ya contiene el programa).
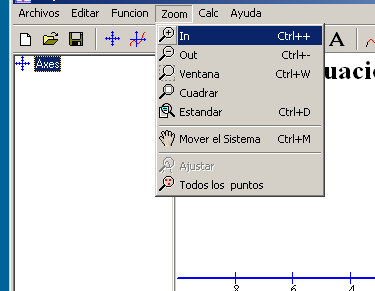
El submenú Zoom nos permite: ampliar, alejar, ampliar una parte señalada (ventana), hacer que los ejes se vean con la misma medida (cuadrar), volver a la representación inicial (estándar), mover libremente los ejes, ajustar la gráfica a nuestra ventana y mostrar todos los puntos.
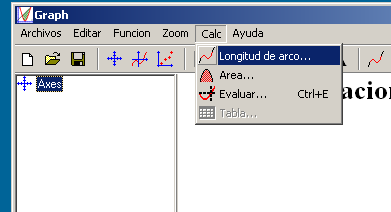
El submenú Calc nos permite: medir la longitud de la gráfica entre dos puntos, calcular un área, conocer el valor de la gráfica en un punto (evaluar) y en una serie de ellos (tabla).
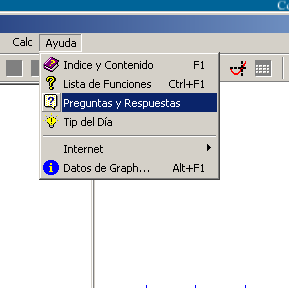
El submenú Ayuda nos permite saber más de este programa: su manual, la lista de funciones que reconoce por defecto, preguntas frecuentes, indicaciones varias, acceso a su página web y la versión de programa.
5.2. Barra de herramientasLa barra de herramientas nos permite acceder a las funciones más utilizadas de los menús del programa. Por orden, de izquierda a derecha y según las divisiones, son:
Nota aclaratoriaNuestro lenguaje científico (español) utiliza la coma (,) como separador para la parte decimal de un número. Por ejemplo: 3,1415 ; 2,12121 ; ... El programa trabaja con la notación científica anglosajona por lo que en vez de usar la coma (,) utiliza el punto (.) para separar la parte decimal. Por ejemplo: 3.1415 ; 2.12121 ; ... Este manual está escrito siguiendo la notación española, por lo que a la hora de trabajar con el programa habrá que cambiar la coma decimal por el punto.
6. Estudio de casos sencillos: constantes y rectas6.1. ConstantesEmpecemos a trabajar con nuestro programa haciendo un ejemplo sencillo mediante una función que valga siempre un mismo valor: a cada punto de la recta real se le asigna siempre como imagen el mismo número, una constante. Nuestra primera función va a ser aquella que a todo punto de la recta real le asigna el número 3, es decir Pulsamos en el botón Insertar una nueva función (el quinto por la izquierda de la barra de herramientas) y nos aparecerá una nueva ventana en la que podremos indicar los parámetros de la función deseada: ecuación, desde que punto a que punto deseamos dibujar la gráfica (el rango), etc. En este caso haremos lo siguiente:
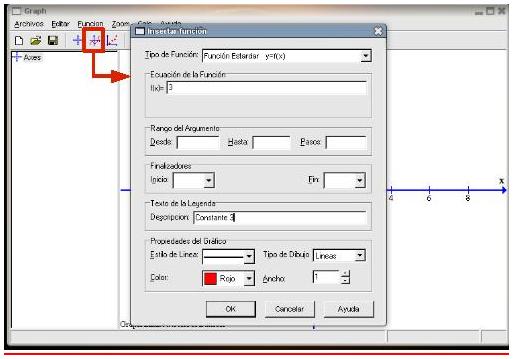
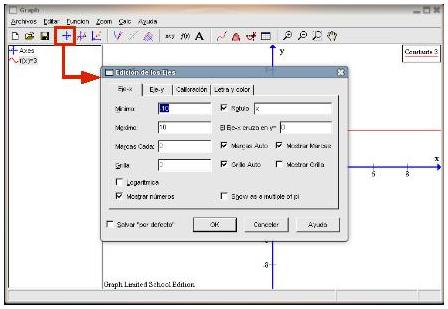
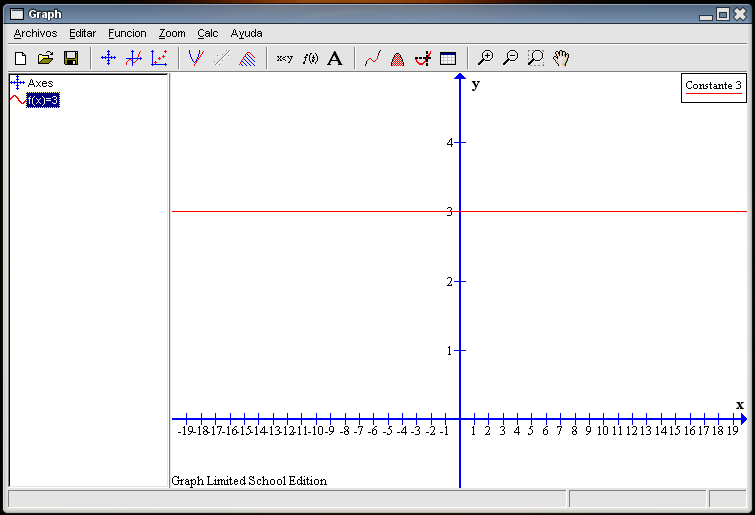
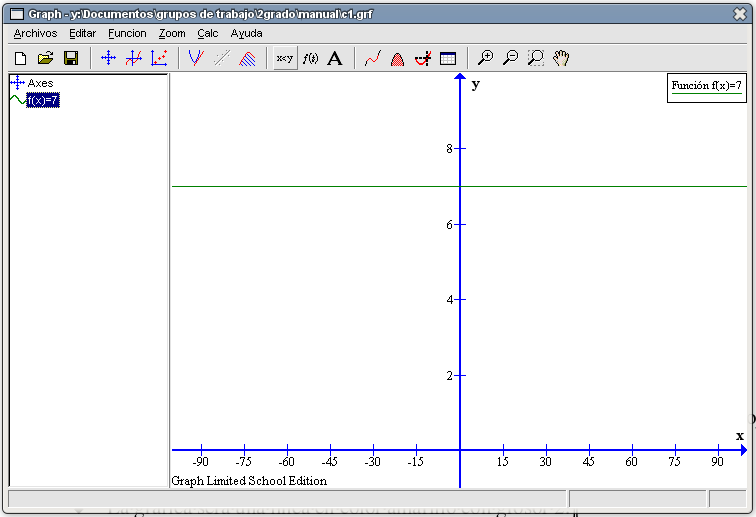
Cuando tengamos rellenos los campos indicados bastará con pulsar en el botón OK para que el programa genere la gráfica. El resultado será similar al que se muestra en la siguiente captura de pantalla. 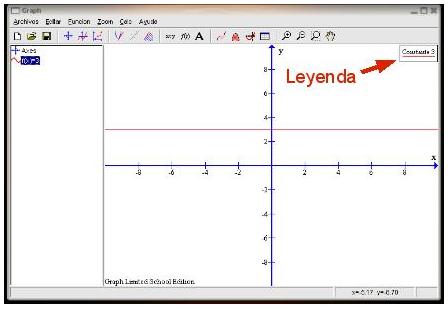 Como podemos observar en la columna izquierda de la ventana aparece la función que hemos trazado y en la parte derecha de la ventana aparece en un rectángulo lo que escribimos en la casilla Texto de la Leyenda. Los ejes que aparecen por defecto, tanto para la variable independiente X como para la variable dependiente Y, van de -10 a 10 haciendo una marca cada 2 unidades. Vamos a modificarlos para que, por ejemplo, sean así:
Pulsamos en el botón de Editar las propiedades de los Ejes (cuarto por la izquierda de la barra de herramientas). También podríamos llegar al mismo sitio utilizando en la barra de menús Editar Ejes... Aparecerá la siguiente ventana:
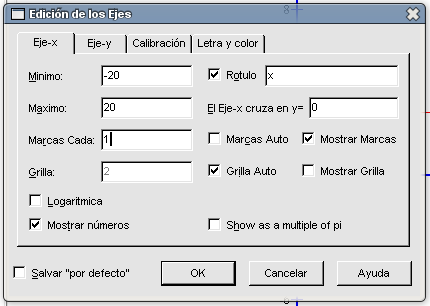
En la pestaña correspondiente al eje X cambiaremos en la casilla Mínimo, -10 por -20; y en la casilla Máximo, 10 por 20. Para que nos muestre una marca cada unidad, quitamos la señal de Marcas Auto y en la casilla Marcas Celda cambiaremos 2 por 1.
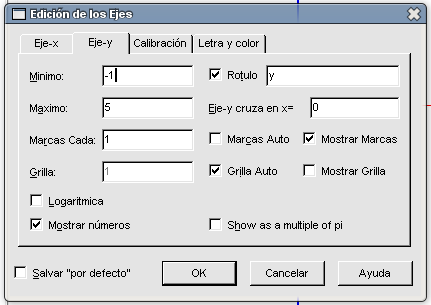
Si hubiéramos elegido para Y como valor mínimo 0 en vez de -1, no aparecerían reflejados los números del eje X.
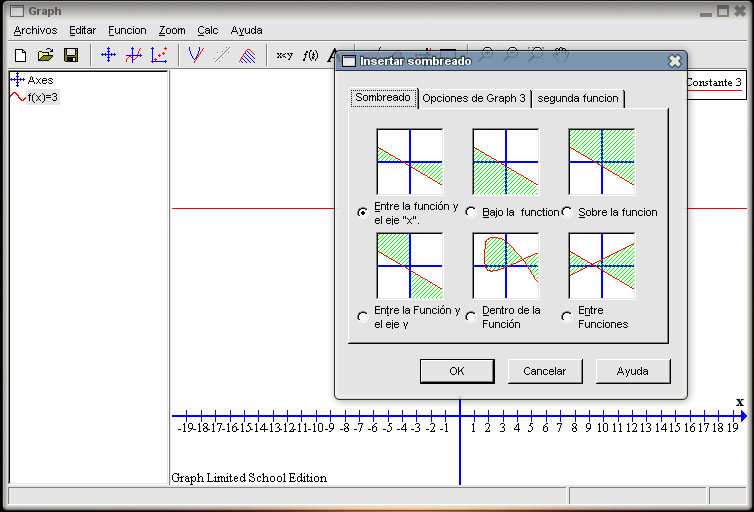
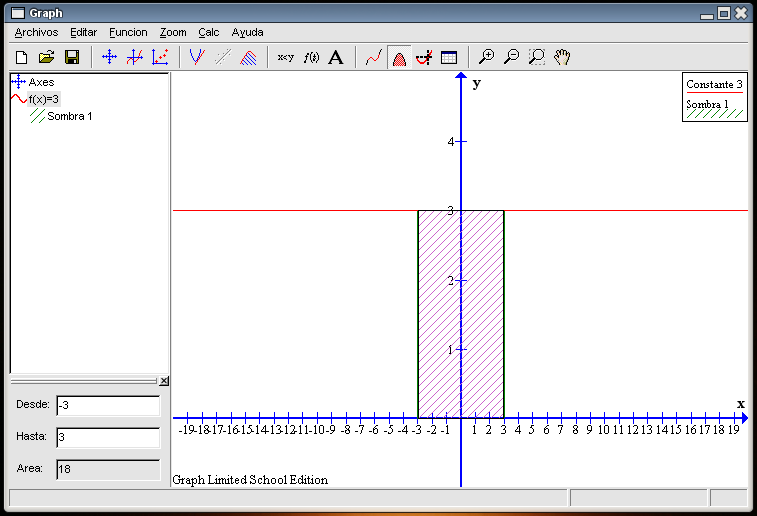
El programa nos permite sombrear partes de la función. Por ejemplo, vamos a sombrear desde el punto -3 al punto 3, el área comprendida entre la función y el eje X. Pulsamos el botón Agregar Sombreado a una Función (noveno desde la izquierda en la barra de herramientas). También podríamos hacer en la barra de menús Función Insertar sombreado. Aparecerá la siguiente ventana:
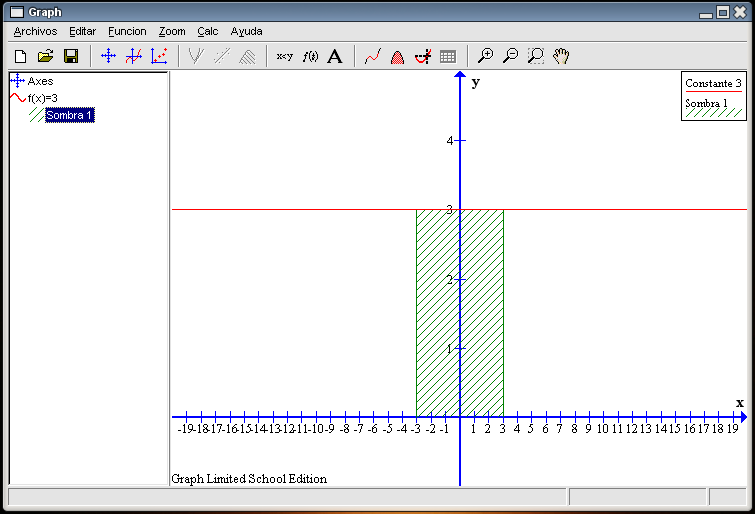
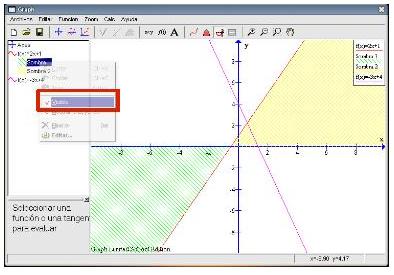
Como lo que deseamos es sombrear la zona entre la función y el eje X, no tenemos que modificar lo que aparece por defecto en la pestaña Sombreado. Para indicar que sólo queremos la zona comprendida entre -3 y 3, en la siguiente pestaña Opciones de Graph 3 rellenaremos las casillas correspondientes al Rango tal y como aparece en la imagen de la derecha. El área se rellenará con líneas oblicuas de color verde, marcándose con una línea tanto el comienzo como el final de la misma. Tras pulsar en el botón OK, la gráfica quedará igual a la que se muestra en la siguiente imagen. La sombra insertada, Sombra1, aparece reflejada en la columna de la izquierda y en la leyenda de la gráfica. Si nos equivocamos en algo, podemos rectificar señalando en la columna de la izquierda Sombra1 y pulsar el botón derecho del ratón. Aparecerá el menú contextual y elegiremos la última opción Editar.
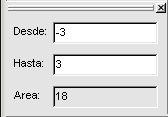
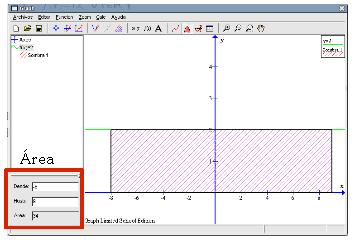
Ya que tenemos sombreada una parte de esta gráfica calculemos el área encerrada en ella. Podemos observar que es un rectángulo cuya base mide 6 unidades (de -3 a 3) y su altura mide 3 unidades (de 0 a 3). El área de esta figura geométrica (un rectángulo) se calcula multiplicado la base por la altura, por lo que en este caso su valor es 6 x 3 = 18 unidades cuadradas. Utilizando el programa también se puede calcular dicha área. Podemos elegir en la barra de herramientas el botón Calcular el área debajo de un segmento de una curva (séptimo por la derecha), o utilizar el menú Calc Área. Teniendo seleccionada la función (en la columna de la izquierda), en la parte inferior izquierda de la ventana principal aparecerá un nuevo recuadro. 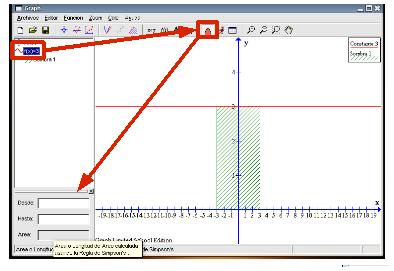 Nuestra área buscada va desde el punto -3 al 3, por lo que:
En la última casilla, Área, se reflejará el tamaño total: 18 unidades cuadradas; resultado que coincide con el que calculamos usando la fórmula tradicional. Observemos que la zona sombreada cambia de color (un tono violeta) para indicar el área que se ha calculado.
Ejercicio 1Para cada una de las siguientes funciones constantes crea su gráfica. Guarda todos los ficheros en tu carpeta de trabajo con los nombres que se indican entre paréntesis.
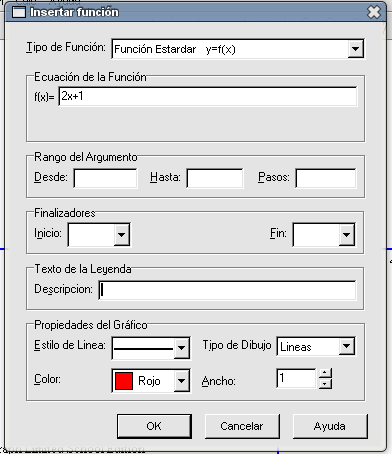
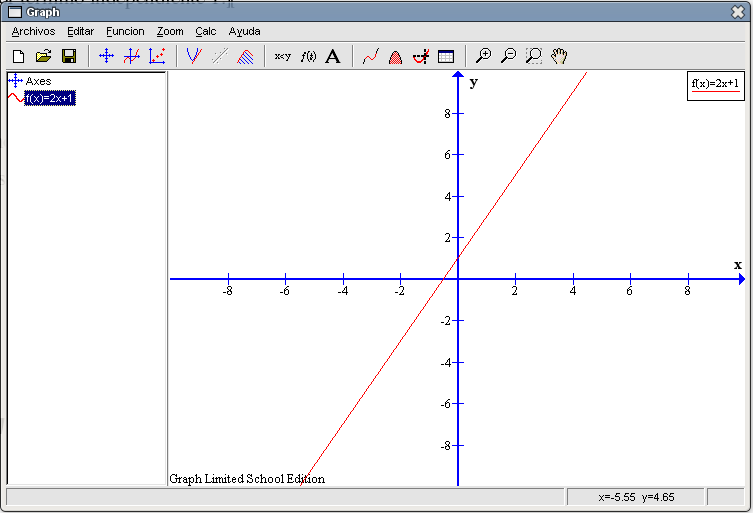
6.2. RectasPasemos a representar gráficamente un par de rectas y conocer un poco más de las posibilidades que nos brinda este programa. Nuestra primera recta va a ser la que tiene por ecuación Creemos una nuevo archivo y al igual que hicimos antes para crear una función constante, pulsemos en el botón Insertar una nueva función (el quinto por la izquierda de la barra de herramientas) para indicar la ecuación de nuestra recta. Sólo rellenaremos la casilla de Ecuación de la Función con el texto
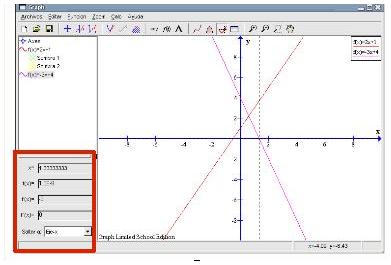
Teniendo seleccionada la ecuación en la columna de la izquierda, pulsemos en el botón Evaluar la función seleccionada (sexto por la derecha en la barra de herramientas). También podríamos acceder a esta función mediante Calc Evaluar.
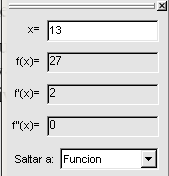
Si quisiéramos saber lo que vale la función para un punto bastaría con escribir dicho valor en la primera casilla y directamente en las siguientes nos aparecería el valor de: la función, la primera derivada y la segunda derivada. Por ejemplo, para el punto Retomemos el origen de la cuestión, averiguar los puntos de corte. Para el corte con el eje Y bastará con escribir 0 en la primera casilla. Obtendremos en el segundo recuadro que
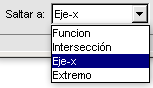
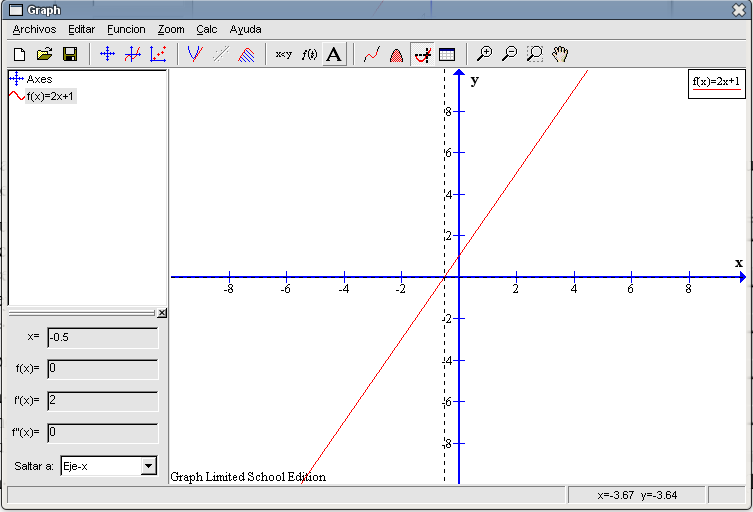
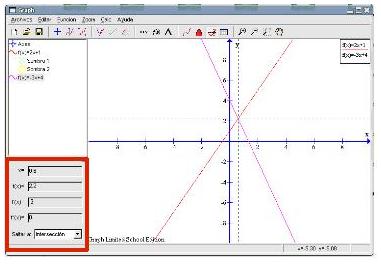
Para el corte con el eje X desplegaremos el menú del final de este recuadro y elegiremos la tercera opción, Eje-x. Al pulsar con el cursor en cualquier parte de la gráfica aparecerá reflejado el valor que buscábamos (-0,5) y en la gráfica se traza una línea vertical de trazos discontinuos que pasa por el punto en cuestión. El punto de corte con el eje X es (-0,5 , 0). Al igual que hicimos con las funciones constantes sombrearemos ciertas partes de esta gráfica y calcularemos algún área. Podemos observar que la gráfica tiene:
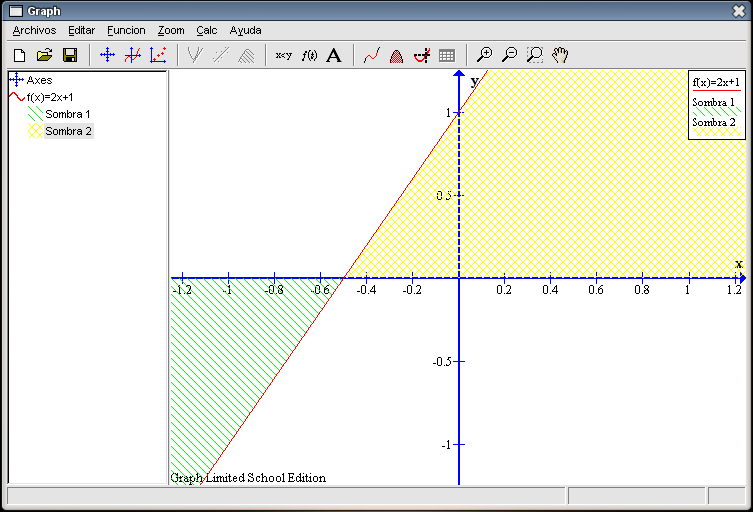
Vamos a sombrear de forma diferente cada una de estas zonas. Por ejemplo, la primera será con líneas oblicuas en color limón y la segunda con rejilla en color amarillo.
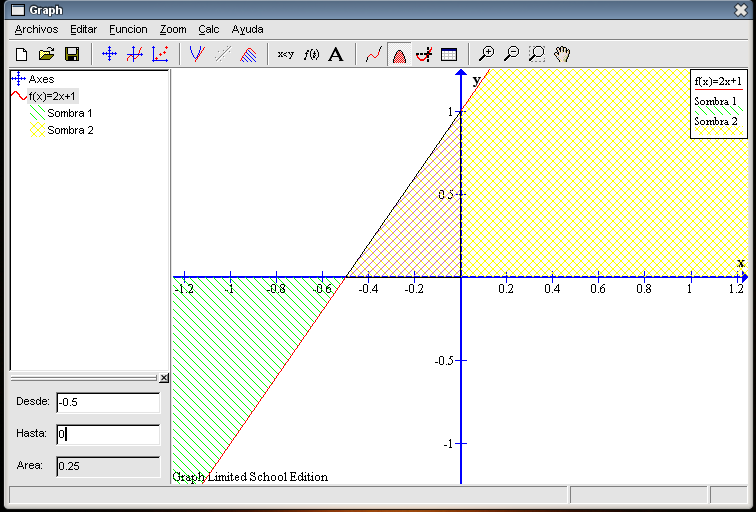
Observando la gráfica (la siguiente imagen es una ampliación) podemos ver que se forma un pequeño triángulo entre la recta y los ejes de coordenadas ¿Cuál será su área?
Gracias en parte a lo que hemos calculado previamente, sabemos que la base de este triángulo va desde el punto (-0,5 , 0) al (0 , 0). Luego, utilizando la herramienta de Área con los valores -0,5 y 0 obtenemos que la extensión de este triángulo es de 0,25 unidades cuadradas.
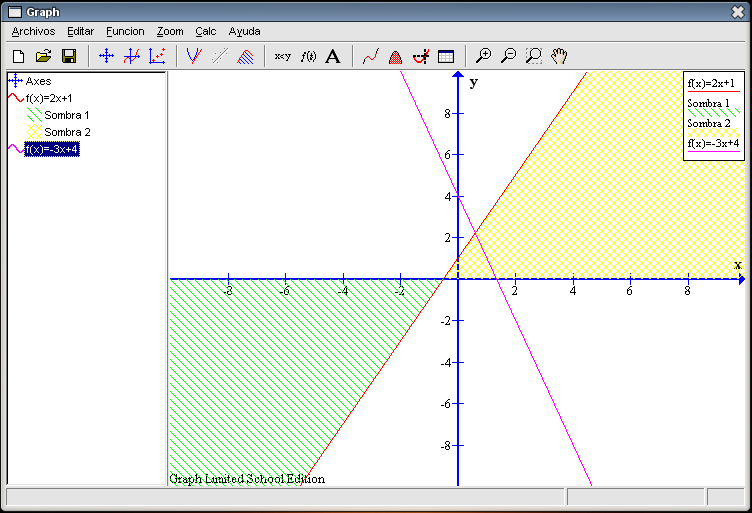
¿Utilizando el programa se podría calcular, por ejemplo, el área que ocupa la Sombra1? La verdad es que no. Mirando la gráfica observamos que no tiene ningún límite inferior, por lo que no es posible rellenar la casilla Desde. Sabemos que su área es infinita puesto que se extiende sin fin por la parte negativa del eje de las X. Vamos a complicar un poco este estudio insertando una nueva recta en esta gráfica y calculando algunos datos. Nuestra segunda recta va a ser la que tiene por ecuación Al igual que antes, pulsamos en el botón Insertar una nueva función (el quinto por la izquierda de la barra de herramientas) para indicar la ecuación de nuestra recta. Sólo rellenamos la casilla de Ecuación de la Función con el texto
Las dos sombras que hemos calculado antes nos pueden molestar mientras trabajamos, por lo que las haremos invisibles. Para ello señalamos, por ejemplo, Sombra1 de la columna de la izquierda y pulsamos el botón derecho del ratón, apareciendo el menú contextual del cual desmarcaremos la opción Visible. Haremos lo mismo con Sombra2.
Calculemos los puntos de corte de la nueva recta:
La opción Evaluar la función seleccionada nos permite calcular algo más. Te habrás dado cuenta que aparte de Función y Eje-x hay otras dos posibilidades: Extremo e Intersección. Probemos esta última dejando para más adelante la otra. Mirando la gráfica observamos que las dos rectas se cortan en un lugar del plano. Hay un punto de intersección entre ellas que tendrá unas coordenadas y que averiguaremos usando la opción Intersección. Teniendo pulsada cualquiera de las dos funciones (columna de la izquierda), elegimos Intersección del menú desplegable y pulsamos en cualquier parte de la gráfica. El resultado buscado, el punto de corte, es (0,6 , 2,2) y aparece marcado en la gráfica mediante la intersección de dos líneas rectas de trazo discontinuo.
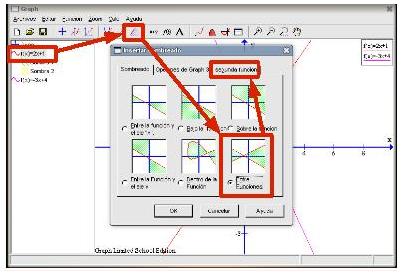
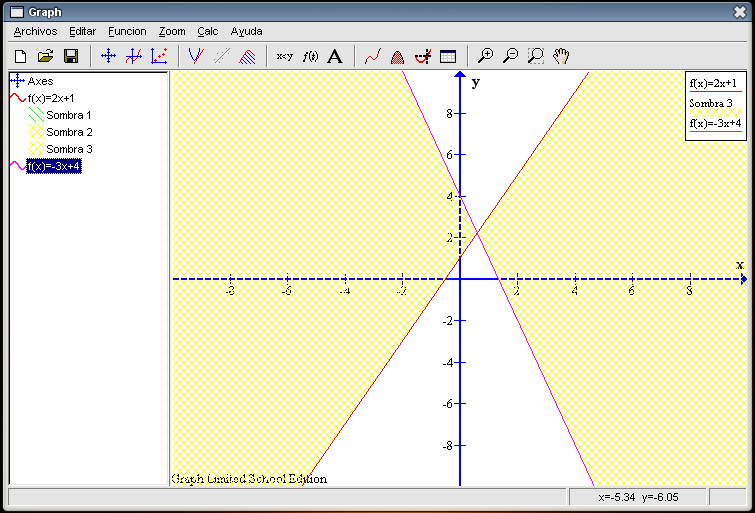
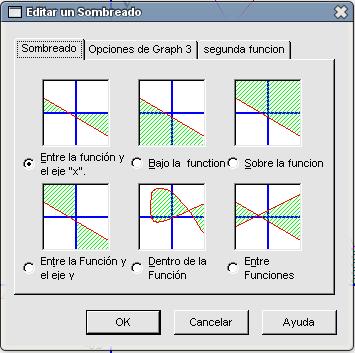
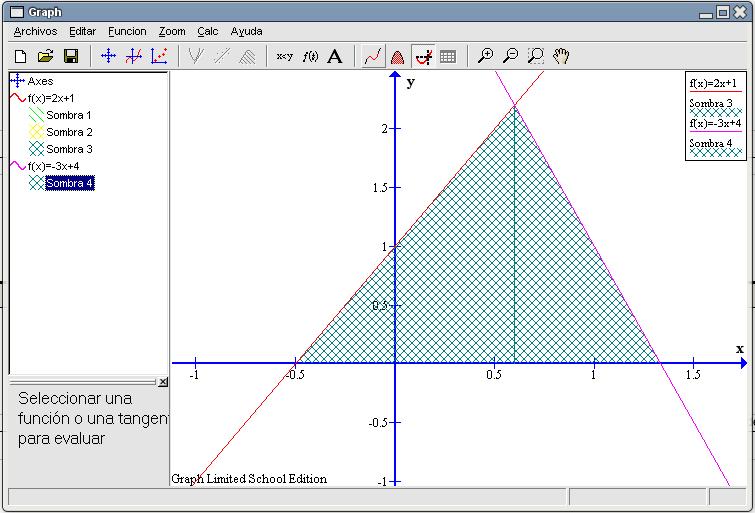
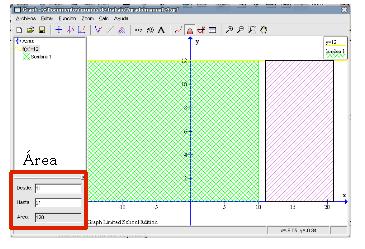
El punto de intersección junto con los respectivos cortes de las rectas con el eje X forman una figura geométrica conocida como triángulo. Para poder verla bien vamos a sombrear dicha zona del plano: señalamos la ecuación de la primera recta en la columna de la izquierda, pulsamos en el botón Agregar sombreado a una función (noveno por la izquierda de la barra de herramientas), en la pestaña Sombreado elegimos la opción Entre funciones y en la pestaña Segunda Función marcamos la otra recta.
Esto no es lo que queremos, ha señalado las zonas comprendidas entre ambas funciones. Habrá que idear otra forma que nos permita sombrear esa región. El triángulo podemos verlo como la unión de otros dos: uno es la zona que comprende la recta Marcamos la recta
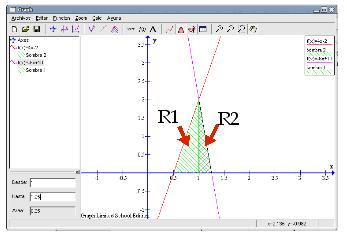
El resultado es el siguiente (ampliando la zona):
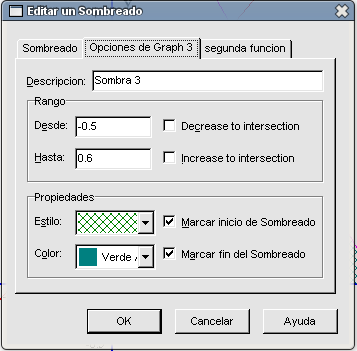
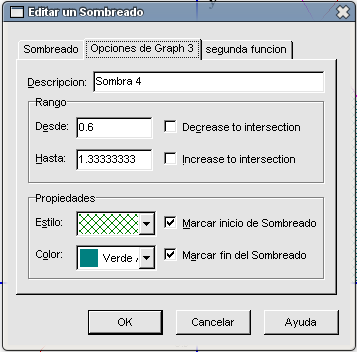
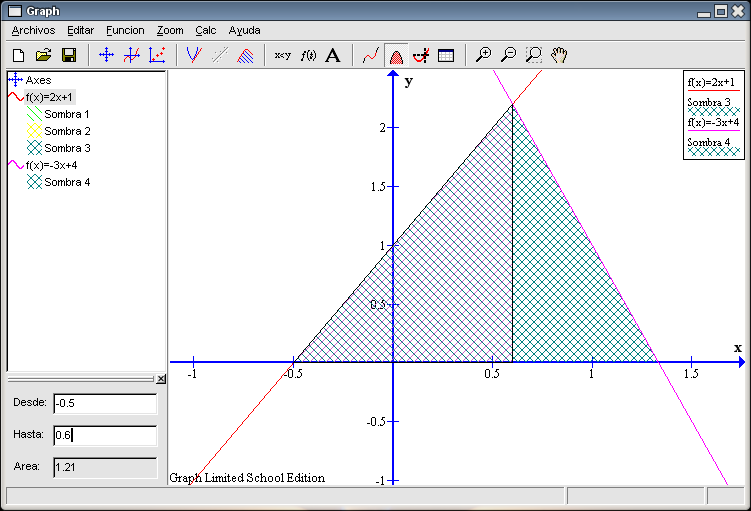
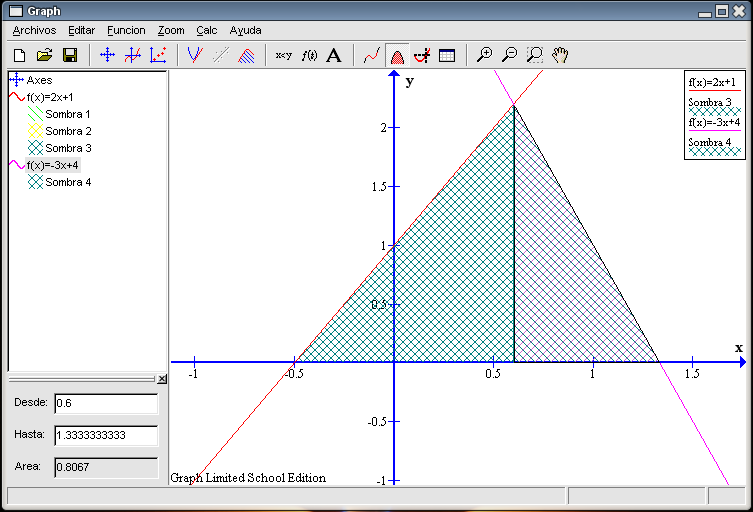
Esta idea de dividir el triángulo principal en dos también nos va a servir para calcular su área: hacemos primero la zona entre -0,5 y 0,6 para la recta Marcamos la recta
1,21 + 0,8067 = 2,0167 unidades cuadradas. Ejercicio 2Para cada una de las siguientes funciones crea su gráfica y realiza lo indicado. Las tramas y colores los dejamos a tu elección. Guarda todos los ficheros en tu carpeta de trabajo con los nombres que se indican entre paréntesis.
SolucionesEjercicio 1
Ejercicio 2
Los puntos de corte con los ejes son (0 , 2) y (4 , 0). f(8) = -2 ; f(-15) = 9,5 ; f(20) = -8 ; f(-23) = 13,5. El área entre 0 y 4 vale 4 unidades cuadradas; entre -9 y -2,5 vale 31,6875 unidades cuadradas. El área entre -4 y -2 vale 7 unidades cuadradas; entre 0 y 8 si lo calculamos directamente sale como resultado 0. Como el área entre 0 y 4 sale positiva (y vale 4 unidades cuadradas) y el área entre 4 y 8 sale negativa (y vale -4 unidades cuadradas), al sumarlas se anulan y por eso sale 0. En verdad el área es siempre positiva (no hay nada en la vida real que tenga un área negativa) por lo que el resultado correcto es 8 unidades cuadradas: 4 de ellas provienen de 0 a 4 y las otras 4 provienen de 4 a 8. 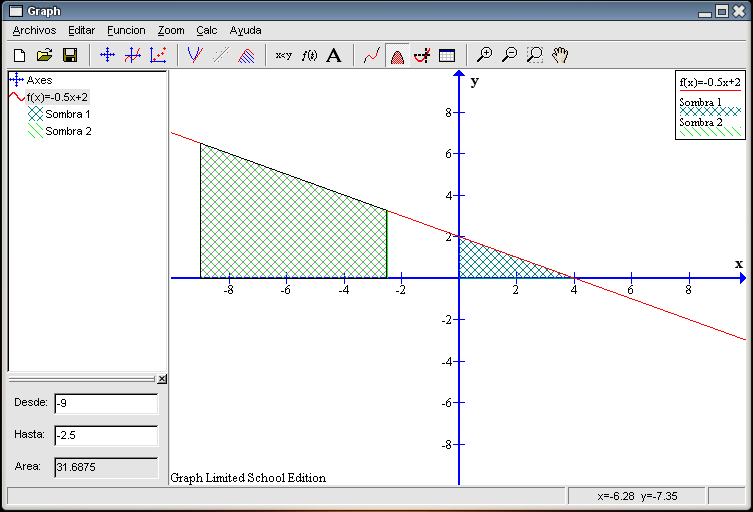
Los puntos de corte para Los puntos de corte para El punto de intersección tiene de coordenadas (1 , 2). El área (R1) para la recta El área (R2) para la recta
Por tanto, el área del triángulo es de: 0,5 + 0,25 = 0,75 unidades cuadradas.
Los puntos de corte para Los puntos de corte para Las coordenadas aproximadas del punto de corte son (2,222222 , -1,6667) El área (R1) para la recta El área (R2) para la recta 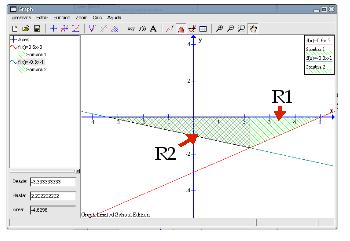
Por tanto, el valor aproximado del área del triángulo es: 2,3148 + 4,6296 = 6,9444 unidades cuadradas.
|