CREACIÓN DE ESCENAS INTERACTIVAS. AUXILIARES
4.9.6. Actividad 4.6
Actividad 4.6
>> Abramos la escena incompleta "trabajo".
> Si pulsamos aceptar podemos comprobar el funcionamiento del algoritmo (procedimiento de integración numérica de Simpson).
ADVERTENCIA: Procure que Xin<Xfin; de lo contrario tendrá un mensaje de error.
> Para un valor de n=10000 se alcanza un resultado similar al de la integración analítica.
> Si hemos operado sin errores hemos debido obtener una escena como
> En realidad, los algoritmos se utilizan mucho en Descartes. Antes los hemos visto utilizar en la animación de escenas y, enseguida, veremos también su uso en otro tipo de variables, las funciones. También debemos señalar que hay algoritmos en los que no hay parte inicio ni parte mientras. En ellos, la parte hacer se realiza una sola vez.
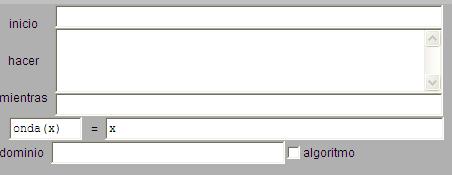
>> Nos planteamos realizar una escena capaz de realizar la superposición de dos ondas. Después de abrir "ondas" observemos sus controles para comprender su significado. El de A1, A2, w1 y w2 es obvio. El control d nos mide el desfase de movimientos. En configuración (hacemos clic de botón derecho) señalamos gráficos y pinchamos en la primera curva. En ella se habla de una función no definida todavía. Entramos en Auxiliares + para agregar una función de nombre onda. Aparecerá una ventana de diálogo:
> En su configuración se pueden ver tres controles (los límites de x y el número de intervalos entre ambos valores) y un gráfico de tipo texto que mostraría el valor de una variable no definida que llamamos trabajo. En auxiliares pulsaremos + para agregar un algoritmo que llamaremos integral. Vamos a ver cómo llenamos su contenido.
| En la línea de inicio |
x=Xin; trabajo =0 |
Así hemos escrito dos nuevas auxiliares separadas por un punto y coma: la posición x que varía entre los extremos del intervalo y el trabajo, inicialmente nulo |
| En hacer |
trabajo=trabajo+100*x*(Xfin-Xin)/n x=x+(Xfin-Xin)/n |
Aumenta la variable trabajo con el producido en cada pequeño intervalo e incrementa la variable x |
| En mientras | x<=Xfin | El algoritmo finaliza cuando x llega al final del interval |
> Si pulsamos aceptar podemos comprobar el funcionamiento del algoritmo (procedimiento de integración numérica de Simpson).
ADVERTENCIA: Procure que Xin<Xfin; de lo contrario tendrá un mensaje de error.
> Para un valor de n=10000 se alcanza un resultado similar al de la integración analítica.
> Si hemos operado sin errores hemos debido obtener una escena como
> En realidad, los algoritmos se utilizan mucho en Descartes. Antes los hemos visto utilizar en la animación de escenas y, enseguida, veremos también su uso en otro tipo de variables, las funciones. También debemos señalar que hay algoritmos en los que no hay parte inicio ni parte mientras. En ellos, la parte hacer se realiza una sola vez.
>> Nos planteamos realizar una escena capaz de realizar la superposición de dos ondas. Después de abrir "ondas" observemos sus controles para comprender su significado. El de A1, A2, w1 y w2 es obvio. El control d nos mide el desfase de movimientos. En configuración (hacemos clic de botón derecho) señalamos gráficos y pinchamos en la primera curva. En ella se habla de una función no definida todavía. Entramos en Auxiliares + para agregar una función de nombre onda. Aparecerá una ventana de diálogo:

>La estructura similar a la de un algoritmo nos sirve en este caso. En la parte donde está el nombre escribamos, en vez de onda(x) la expresión onda(A,w,d,t) y, al otro lado de la igualdad, sustituimos la x por A*sen(w*t+d). La función está definida. Si volvemos a gráficos, vemos que en las curvas se aplica esta misma función para cada curva y para la resultante. Pulsemos aceptar y comprobemos el resultado.
El uso de funciones también es muy conveniente cuando las operaciones para dar valor a una variable son complicadas.
Podemos ver la actividad resuelta
El uso de funciones también es muy conveniente cuando las operaciones para dar valor a una variable son complicadas.
Podemos ver la actividad resuelta