CREACIÓN DE ESCENAS INTERACTIVAS. AUXILIARES
4.9.5. Actividad 4.5
Actividad 4.5
>> Vamos a afrontar el problema de introducir muchos vectores en una escena. Observemos la escena incompleta "Muchos vectores".
> Entrando en su configuración (hacemos clic de botón derecho), notamos que, en controles, hay dos componentes, x e y, numéricos. En gráficos está definida una familia de 12 flechas (número de pasos), con orígenes orx[s] y ory[s], extremos en finx[s]y finy[s], con el parámetro s variando entre 0 y 11. Mirando en auxiliares, vemos que están definidos estos vectores, aunque sin darles valores. En auxiliares, pulsamos + para agregar un componente de tipo algoritmo, que llamaremos valores. Se abre una ventana como esta:
> Entrando en su configuración (hacemos clic de botón derecho), notamos que, en controles, hay dos componentes, x e y, numéricos. En gráficos está definida una familia de 12 flechas (número de pasos), con orígenes orx[s] y ory[s], extremos en finx[s]y finy[s], con el parámetro s variando entre 0 y 11. Mirando en auxiliares, vemos que están definidos estos vectores, aunque sin darles valores. En auxiliares, pulsamos + para agregar un componente de tipo algoritmo, que llamaremos valores. Se abre una ventana como esta:
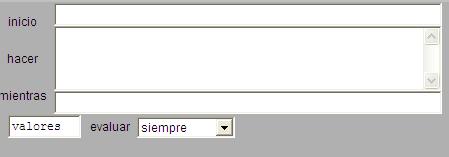
En inicio escribimos s=0 (empezamos con el vector 0). En hacer escribimos: orx[s]= (s-4)/3
ory[s]= (s-4)/3
finx[s]=orx[s]+x
finy[s]=ory[s]+y
s=s+1
Así damos valores a orígenes y extremos de la flecha cero y pasamos a la siguiente con la última línea (s=s+1).
Finalmente, en el apartado mientras escribimos s<= 11
Así significamos que cuando s sea 11, estaremos en el último vector y se detendrá el algoritmo. Pulsemos aceptar.
Nos habrá quedado algo como esta actividad resuelta.
>> Un algoritmo puede servir también para realizar cálculos complejos. Supongamos que deseamos que el ordenador calcule el trabajo que hace la fuerza F=100·X cuando una partícula va desde el punto inicial Xin hasta el punto final Xfin. Como la fuerza es variable a lo largo de x no podemos simplemente multiplicar F por el desplazamiento (Xfin-Xin). Como el ordenador, igual que nuestros alumnos, no sabe integrar. El procedimiento más intuitivo es dividir el desplazamiento en fragmentos muy pequeños, en los que F sea prácticamente constante.
ory[s]= (s-4)/3
finx[s]=orx[s]+x
finy[s]=ory[s]+y
s=s+1
Así damos valores a orígenes y extremos de la flecha cero y pasamos a la siguiente con la última línea (s=s+1).
Finalmente, en el apartado mientras escribimos s<= 11
Así significamos que cuando s sea 11, estaremos en el último vector y se detendrá el algoritmo. Pulsemos aceptar.
Nos habrá quedado algo como esta actividad resuelta.
>> Un algoritmo puede servir también para realizar cálculos complejos. Supongamos que deseamos que el ordenador calcule el trabajo que hace la fuerza F=100·X cuando una partícula va desde el punto inicial Xin hasta el punto final Xfin. Como la fuerza es variable a lo largo de x no podemos simplemente multiplicar F por el desplazamiento (Xfin-Xin). Como el ordenador, igual que nuestros alumnos, no sabe integrar. El procedimiento más intuitivo es dividir el desplazamiento en fragmentos muy pequeños, en los que F sea prácticamente constante.