4.5. Funciones y sucesiones
>Funciones.
Como en Matemáticas, una función es el resultado de realizar ciertas operaciones con una variable. En Descartes, detrás del nombre de la función, va un paréntesis y, separadas por comas, las variables de que depende. Las funciones asignan un número real a cada valor de su variable (o a cada conjunto de valores de sus variables). Las funciones tienen un identificador (o nombre), una o más variables (que no son más que una lista de identificadores) y una expresión en términos de esas variables. Por ejemplo, la fuerza de fricción del aire sobre un cuerpo depende de su tamaño, velocidad y coeficiente de forma y se podría definir como F(r, v, k) donde r, v y k corresponden a las variables indicadas.
Estos son ejemplos de funciones de una variable con sus identificadores y sus variables:
|
expresión |
identificador |
variable |
| f(x)=sen(3*x+2) | f | x |
| g(y)=A*exp(-(y^2)/(s^2)) | g | y |
| Area(radio)=(pi*radio^2)/2 | Area | radio |
Estos son ejemplos de funciones de dos o más variables con sus identificadores y sus variables:
|
expresión |
identificador |
variables |
| f(x,y)=raíz(x^2+y^2) | f | x,y |
| Fun(x,y,z) | Fun | x,y,z |
| Volumen(a,b,c)=4*pi*a*b*c/3 | Volumen | a,b,c |
Los nombres específicos de las variables de una función no son importantes, sólo sirven para identificar las variables dentro de la expresión y asignarles allí un papel.
Las funciones se evalúan nada más cuando son llamadas explícitamente (por ejemplo por un algoritmo, por un gráfico, por la animación o por la constricción de un control gráfico que se mueve).
El panel de configuración de una función tiene este aspecto:
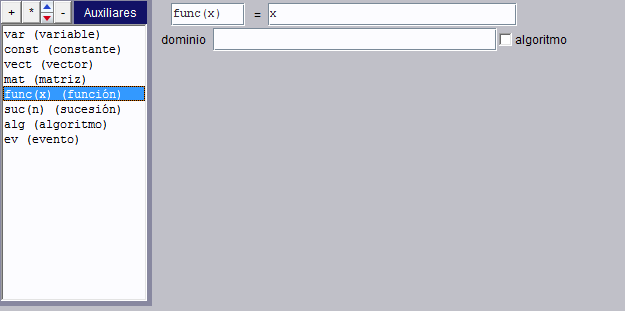
|
id
|
Es el identificador del auxiliar. En el caso de una función o algoritmo debe incluir los parámetros de los que dependa escritos entre paréntesis y separados por comas. Por ejemplo: f(x,y,x). |
|
evaluar |
Es un selector con dos posibles valores: siempre o una_sola_vez. Permite definir si la constante, la expresión del vector o el algoritmo deben evaluarse cada vez que el usuario modifica un control o sólamente una vez al iniciarse la escena. Es importante seleccionar una_sola_vez cuando sea factible para que el funcionamiento de la escena sea más rápido. |
|
dominio |
Es una expresión booleana que determina el dominio de la función. Cualquier intento de evaluar la función fuera de su dominio lanzará una excepción, con lo cual, por ejemplo, su gráfica no se dibuja en los puntos que no están en el dominio. El valor por defecto es vacío, lo cual se interpreta como que el dominio no está restringido. |
|
algoritmo |
Selector que indica si la función, para evaluarse, debe usar un algoritmo; es decir, si necesita los cálculos indicados en "inicio", "hacer" y "mientras". |
|
inicio
|
En el campo "inicio" puede escribirse una serie de asignaciones y llamadas a algoritmos separadas por ; Todo lo que haya en este campo se ejecuta al inicio del cálculo. |
|
hacer
|
En el campo "hacer" puede escribirse una serie de asignaciones y llamadas a algoritmos separadas por saltos de línea. Lo que hay en "hacer" se ejecuta repetidamente mientras la condición "mientras" sea válida. |
|
mientras
|
En el campo "mientras" se debe escribir una expresión booleana.
Lo que hay en "hacer" se ejecuta repetidamente mientras la |
El campo donde aparece el identificador de la función (a la izquierda del signo = ) debe incluir los identificadores de las variables entre paréntesis y separados por comas, para dar sentido a la expresión que aparece al lado derecho. La expresión que aparece a la derecha del signo = puede ser, o incluir, un término condicional, por ejemplo:
func(x)=(x<0)?0:1.
es la función que vale 0 para x<0 y 1 para x>=0. Una expresión booleana vale 1 cuando es verdadera y 0 cuando es falsa por lo cual la función anterior también podría escribirse como
func(x)=(x>=0),
o bien usando la función indicadora ind, también podría escribirse como:
func(x)=ind(x>=0),
Al final de esta página se ofrece una lista de todas las funciones matemáticas y los operadores que reconoce el analizador de expresiones de Descartes, aparte de las que se definen explícitamente en cada escena. Estas funciones y operadores pueden usarse en cualquier sitio donde Descartes espera una expresión, incluyendo el campo de texto de un control numérico.
El dominio puede ser una expresión booleana en términos de las variables de la función. El programa utiliza el dominio para decidir si intenta evaluar la función. Si en un punto la expresión del dominio no se cumple, la evaluación no se intenta y el programa genera una excepción, con lo cual, si se está dibujando por ejemplo la gráfica de esta función, el dibujo que corresponde a este punto no se realiza y se pasa al siguiente. Cuando el campo del domino está vacío se considera que el dominio de la función no tiene restricciones, es decir, cualquier conjunto de valores de sus variables está en el dominio.
Cuando el programa intenta evaluar una función en un punto donde tiene una singularidad, se genera una interrupción, igual que si el punto no estuviera en el dominio. Por lo tanto no es necesario excluir del dominio de una función sus puntos singulares, el programa ya lo hace automáticamente. Sólo hay que especificar el dominio si se desea restringir el dominio natural de una función.
A veces no se puede definir una función solamente mediante una expresión, sino que su evaluación requiere un proceso más complicado. En estos casos el autor puede marcar algoritmo, con lo cual la evaluación de la función realiza antes el algoritmo definido en los campos de texto etiquetados con inicio, hacer y mientras (consultar Algoritmos para el significado de estos términos). En estos campos el autor puede describir el algoritmo de evaluación de la función. El siguiente ejemplo muestra cómo puede una función utilizar un algoritmo. Se trata de una función Fact(x) factorial que calcula el del mayor entero menor o igual que x, para x>=0.
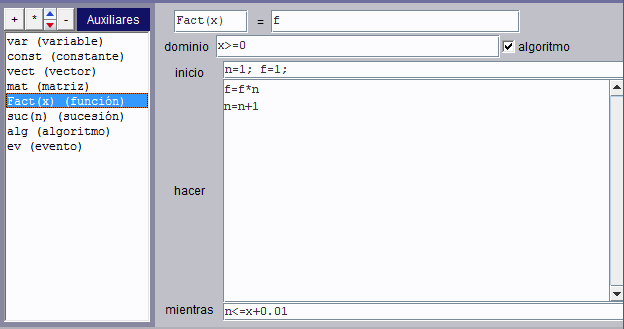
El algoritmo que se define en este panel se ejecuta cada vez que se quiere evaluar la función, por lo cual los valores calculados en el algoritmo pueden utilizarse para definir el valor de la función.
Las funciones pueden tener cualquier número de variables, incluso cero. Para evaluar una función sin variables se debe escribir un par de paréntesis después de su nombre (por ejemplo func()). Las funciones sin variables pueden servir como algoritmos de cálculo que devuelven un valor real. También puede haber funciones que no devuelven ningún valor, las cuales pueden usarse como algoritmos que admiten parámetros. En el ejemplo siguiente se presenta una función de siete variables Euler(x,y,vx,vy,ax,ay,dt) llamada Euler, que en realidad es una implementación del método de integración de Euler para calcular la posición de una partícula que parte de la posición (x,y) con una velocidad (vx,vy) y que se mueve con aceleración constante (ax,ay) durante un tiempo dt y mientras y>0.
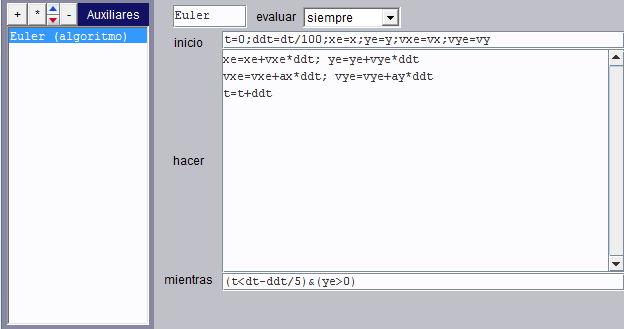
Esta función puede llamarse desde cualquier otra función, desde un algoritmo o desde la animación y al llamarla no hay que asignarla a una variable, basta escribir su nombre y los parámetros que se le pasan separados por comas
Una sucesión es un tipo especial de función, definida sólo para una variable entera. Si la variable no es entera, la sucesión dará un mensaje de error.
Se presentan como complemento las actividades 4.6, 4.7 y 4.8.
En Descartes hay funciones predefinidas. En la siguiente lista están algunas de las más importantes:
Funciones de una variable (x):
sqr sqr(x)=x*x
sqrt sqrt(x)=raíz cuadrada de x
raíz sqrt(x)=raíz cuadrada de x
exp exp(x)=exponencial natural de x=e^x
log log(x)=logaritmo natural de x
log10 log10(x)=logaritmo base 10 de x
abs abs(x)=valor absoluto de x
ent ent(x)=mayor entero n tal que n<x
sgn sgn(x)=signo de x (1 si x>0,-1 si x<0,0 si x=0)
ind ind(b)=indicadora de b (1 si b=true, 0 si b=false)
sin sin(x)=seno de x
sen sen(x)=seno de x
cos cos(x)=coseno de x
tan tan(x)=tangente de x
cot cot(x)=cotangente de x
sec sec(x)=secante de x
csc csc(x)=cosecante de x
sinh sinh(x)=seno hiperbólico de x=(exp(x)-exp(-x))/2
senh senh(x)=seno hiperbólico de x=(exp(x)-exp(-x))/2
cosh cosh(x)=coseno hiperbólico de x=(exp(x)+exp(-x))/2
tanh tanh(x)=tangente hiperbólica de x=sinh(x)/cosh(x)
coth cot(x)=cotangente hiperbólica de x=cosh(x)/sinh(x)
sech sech(x)=secante hiperbólica de x=1/cosh(x)
csch csch(x)=cosecante hiperbólica de x=1/senh(x)
asin asin(x)=ángulo cuyo seno es x
asen asen(x)=ángulo cuyo seno es x
acos acos(x)=ángulo cuyo coseno es x
atan atan(x)=ángulo cuyo coseno es x
Funciones de dos variable (x,y):
min min(x,y)=mínimo de x e y
max max(x,y)=máximo de x e y
También hay un número aleatorio con distribución uniforme en el intervalo [0,1]:
rnd
>Sucesiones
Una sucesión es una función con dominio en los enteros (negativos y no negativos). Por tanto si se intenta evaluar con la variable distinta de un entero, da el error: "función no definida".
El panel de edición de una sucesión es idéntico al de una función y por tanto permite especificar su dominio, que siempre será un subconjunto de los números enteros, y también permite definir sus valores a través de un algoritmo.
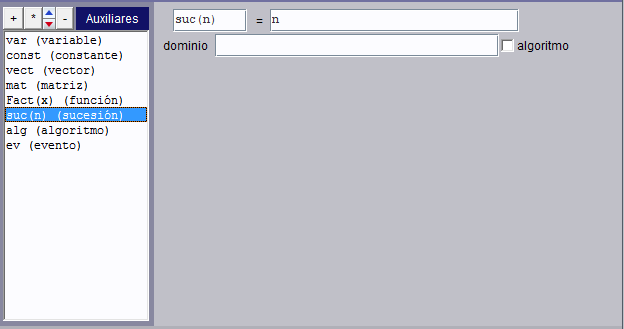
|
id
|
Es el identificador del auxiliar. En el caso de una función o algoritmo debe incluir los parámetros de los que dependa escritos entre paréntesis y separados por comas. Por ejemplo: f(x,y,x). |
|
expresión
|
Es un campo de texto donde debe escribirse la expresión mediante la cual se define el valor de la constante, variable o función |
|
dominio |
Es una expresión booleana que determina el dominio de la función. Cualquier intento de evaluar la función fuera de su dominio lanzará una excepción, con lo cual, por ejemplo, su gráfica no se dibuja en los puntos que no están en el dominio. El valor por defecto es vacío, lo cual se interpreta como que el dominio no está restringido. |
|
algoritmo |
Selector que indica si la función, para evaluarse, debe usar un algoritmo; es decir, si necesita los cálculos indicados en "inicio", "hacer" y "mientras" |
Pondremos un ejemplo muy sencillo de función, para que se vea como funcionan en las escenas.
Las sucesiones funcionan igual que las funciones, pero teniendo en cuenta que las variables deben de tener valores enteros.
Tenemos una función que lo que hace es redondear la cifra introducida. Observese como se construye la escena.
Ahora pondremos un ejemplo de utilización de sucesiones. Mediante una escena se realizará la representación gráfica de la sucesión de números impares (2n+1).