Recursos didácticos 2.0 para matemáticas
 |
Educación Primaria 2º y 3º ciclo |
 |
Matemáticas |
 |
José Ignacio Miguel Díaz |
 |
|
El material didáctico consiste en esencia en una serie de applets interactivos creados con el programa "Geogebra", para trabajar el área de matemáticas, fundamentalmente el bloque de geometría, en el segundo y tercer ciclo de educación primaria. En cada applet aparecen diferentes figuras y elementos geométricos sobre los que podemos interactuar para cambiar su forma, situación en el plano, etc., permitiendo que el alumnado estudie y deduzca las características de esos elementos geométricos mediante el movimiento de los mismos, procedimiento imposible de realizar con los recursos estáticos, es decir, con imágenes en papel. También podemos utilizar estas figuras sencillamente para realizar explicaciones en nuestras clases, sin más que pinchar en el enlace correspondiente, ayudados de un proyector conectado al ordenador o muchísimo mejor con la ayuda de una PDI. Posteriormente describiremos algunos ejemplos de utilización de los applets, con diferentes niveles de aplicación. El único requisito necesario es una conexión a Internet y tener instalado Java.
Las actividades han sido creadas con el programa “Geogebra”, software libre para matemáticas. Este programa tiene múltiples opciones que no son adecuadas para la etapa de Educación Primaria, puesto que esta etapa no ha sido su objetivo inicial, pero siempre podemos realizar las adaptaciones adecuadas que nos permitan trabajar con este software, ya que la interactividad que nos ofrece es lo suficientemente importante como para que hagamos ese esfuerzo. No obstante, si lo que deseamos es sencillamente utilizar las aplicaciones interactivas ya creadas para apoyo de nuestras explicaciones en clase, no necesitamos en absoluto conocer este programa, aunque sin duda alguna el saber utilizarlo nos abre muchas más posibilidades de trabajo en el aula.
JUSTIFICACION
¿Qué creen que nos dirán los alumnos sobre la imagen que está a continuación? Imaginemos que ya hemos estudiado las definiciones y características de diferentes figuras geométricas en el plano y además hemos comprobado que la gran mayoría del alumnado de la clase ya las conoce; vamos a comprobar la puesta en práctica de esos conocimientos adquiridos. Para ello dibujamos en la pizarra o pasamos una fotocopia con la figura que mostramos a continuación, para que el alumnado nos diga su nombre.
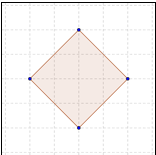La imagen tiene como fondo una trama cuadriculada para ayudar al alumnado a emitir una respuesta correcta y evitar cualquier tipo de confusión o interpretación errónea, por lo que en principio no debería de existir ningún tipo de dificultad para que emitiesen la respuesta correcta, pero seguro que ya sabemos el error que van a cometer y la respuesta que van a dar, a pesar de que “sepan” las características de las dos figuras geométricas: cuadrado y rombo. ¿A qué se debe que la mayoría del alumnado cometa el mismo error? Seguro que se podrían poner muchos ejemplos similares. Creo que el trabajar en geometría con imágenes estáticas, sean del tipo que sean, está condicionando los aprendizajes del alumnado, incluso sin percatarnos de ello, y en contenidos relacionados con la geometría esto puede tener una importancia decisiva.
DIFERENTES NIEVELES DE UTILIZACIÓN DE LOS MATERALES
Los materiales se pueden utilizar en diferentes niveles que pasamos a describir en orden de menor a mayor dificultad y necesidades formativas del profesorado:
Primer nivel.- Utilización de los applets como base de la explicación en clase. Basta disponer de un ordenador, proyector y conexión a Internet. También hemos de tener instalado Java como decía anteriormente. No se necesitan más recursos, aunque si trabajamos con PDI, las explicaciones pueden resultar más explícitas, pues el alumnado ve mucho mejor la forma de interactuar con los elementos geométricos.
Segundo nivel.- En este segundo nivel podemos plantear a nuestro alumnado actividades de investigación. Se trata de utilizar como estrategia el aprendizaje por descubrimiento guiado, pues en todo momento nosotros sabemos el funcionamiento del applet y los posibles descubrimientos que puede realizar el alumnado. Los recursos técnicos y formativos son los mismos que en el nivel anterior, salvo que ahora el alumno va a interactuar con el applet y por tanto necesitará un ordenador. También hemos de organizar la actividad de clase pensando en la forma en la que el alumnado va a trabajar con ese applet: elaboración de preguntas, (algunos applets tienen incorporados varios ejemplos), conclusiones, trabajo en equipo, etc. El cambio en los aprendizajes del alumnado puede ser importante, puesto que los conocimientos se van a adquirir mediante una investigación activa, probando, deduciendo, ..., y no solamente “viendo”, lo que representa un cambio sustancial en los mismos. Se trata pues de una paso más en ese camino desde el "saber" al "saber hacer".
Tercer nivel.- Se trataría de crear nuestros propios applets. Evidentemente se necesita un nivel de formación un poco mayor, puesto que ya debemos conocer el programa Geogebra, pero si lo vemos interesante, lo cierto es que no resulta difícil, pues se trata de un programa muy intuitivo. En este caso ya necesitaremos algo de formación y un poco más de tiempo de dedicación, aunque la ventaja será que podremos hacer nuestras propias construcciones y a gusto de nuestras necesidades personales. El programa, como ya hemos comentado anteriormente, es software libre y nos permite crear applets para cualquier nivel educativo.
Cuarto nivel.- El alumnado realiza sus propios applets. Se trata sin duda alguna del nivel más ambicioso, pero muy asequible tanto para el profesorado como para el alumnado en general. Para ello deberemos mostrar al alumnado algunas de las características del programa y enseñarles a crear y exportar sus propios applets. Además es conveniente pensar en la ubicación de los mismos, puesto que la motivación del alumnado será mucho mayor si ve publicadas sus actividades. El blog de clase puede ser una buena opción. En nuestro caso hemos utilizado Blogger y el alumnado ha colocado sus propias creaciones en su blog personal, que está unido al blog de clase.
UBICACION DE LOS RECURSOS DE GEOMETRIA
Los applets están en dos páginas web:
Los applets presentes en esta página han sido realizados con Geogebra. En estos momentos hay unos cuarenta applets interactivos, la mayoría de geometría para el tercer ciclo del educación primaria, pudiendo utilizarse también adaptar algunos para el segundo ciclo.
Esta página ya tiene algunos años, pero se mantiene pues hay bastantes usuarios de la misma. El planteamiento didáctico es el mismo, pero está realizado con un programa de geometría dinámica denominado “Cabri”, también muy interesante, pero que no es de software libre.
En cuanto se les muestra a los alumnos algún applet, rápidamente se ven atraídos por el programa, ya que pueden mover las figuras, cambiarles el tamaño, modificar su ubicación, interactuar sobre sus elementos notables, etc. De ahí a que posteriormente realicen sus propias construcciones, solamente hay un paso y cuando las en su blog y comprueban que sigue manteniendo esa interactividad, ya no tenemos que hacer mucho más para conseguir motivarles y que se sientan atraídos por esta herramienta. En todo caso e independientemente del nivel de trabajo que hayamos seleccionado de los cuatro mencionados anteriormente, hemos de tener en cuenta que los aprendizajes del alumnado serán más ricos cuanto más experimenten, construyan y analicen por ellos mismos.
En nuestro caso concreto hemos trabajado en los cuatro niveles mencionados anteriormente, siendo el último de ellos, es decir, la elaboración de applets por parte del alumnado el que nos parece más interesante.
Para que el alumnado pudiese construir sus propios applets, lo primero que hicimos fue descargar e instalar el programa “Geogebra” en sus ordenadores y actualizar “Java”. Posteriormente les comentamos muy brevemente el funcionamiento del mismo: sus características, la forma de construir una línea, un polígono y poco más. Posteriormente iban construyendo diferentes figuras geométricas de manera que, a la vez que iban adquiriendo y practicando con diferentes elementos geométricos, también vamos profundizando en el conocimiento del programa: barra de herramientas, modos de exportar, etc. No obstante una de las características del programa es su interactividad inmediata, lo que es sin duda alguna una valiosa herramienta de motivación ya que les permite construir figuras, jugar con ellas, cambiar la forma, descubrir posibilidades, etc., cuestiones que no pueden hacer, o desde luego sería de forma mucho más laboriosa y engorrosa, con figuras estáticas.
Para iniciar al alumnado en el trabajo con este programa hemos diseñado el "Proyecto Geotico", que consiste básicamente en tomar como centro de interés un robot: "Geotico", para posteriormente crear con Geogebra diferentes figuras relacionadas con el mismo. En el proyecto comenzamos construyendo una figura simétrica al robot "Geotico", basado en cuadriláteros, posteriormente dibujamos su nave, "la nave de Geotico", que ya está formada por diferentes polígonos irregulares, su familia, en la que las figuras deben tener unas dimensiones (cuadrículas) determinadas, la parcela de terreno, sobre la que tuvieron que construir diferentes cuadriláteros para medir su superficie, ya que ésta es un polígono irregular, etc. Mediante la construcción de estas figuras vamos trabajando los contenidos de geometría que nos interesan.
También realizaron otras figuras como circunferencias con sus elementos notables, clases de triángulos, de forma que se puedan mover sus vértices pero que deben seguir perteneciendo a esa clase determinada, trabajos con alturas, mediatrices, etc. y además, cuando ya tenían un cierto conocimiento del programa, también realizaron construcciones geométricas "libres", normalmente con movimiento, como composiciones artísticas.
EJEMPLOS DE ACTIVIDADES
EL ROBOT GEÓTICO
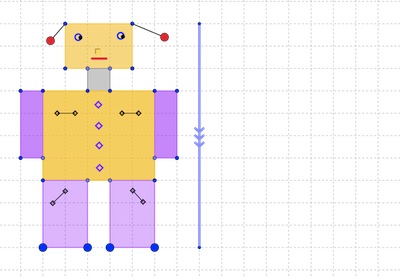
Se trata de familiarizarse con la herramienta. Como se puede ver en la figura, el robot estará formado por cuadrados y rectángulos. Los alumnos han de realizar un robot simétrico a la parte de la derecha. En el applet, si pinchamos en la nariz del robot aparece su simétrico a la derecha, con lo que pueden hacer la comparación con la figura que hayan realizado.
LA PARCELA GEÓTICA
Partimos de una parcela con forma de polígono irregular y tenemos que calcular cuantas cuadrículas tiene, es decir, la superficie de la misma. El problema será el medir o contar el número de cuadrículas que no están enteras, para lo cual los alumnos han de construir diferentes cuadrados y rectángulos que, colocados sobre esas cuadrículas incompletas formen otras figuras que nos permitan medir esa zona. En la figura vemos la parcela original y la solución del problema.
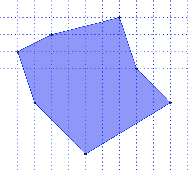
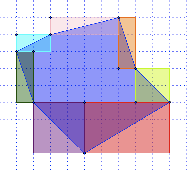
Medida de la parcela:
- Parcela = mitad de tres + mitad de cuatro + mitad de quince + mitad de nueve + mitad de tres + mitad de dos + mitad de cuatro + cuadrículas enteras de la zona central.
- Parcela = 1,5 + 2 + 7,5 + 4,5 + 1,5 + 1 + 2 + 21
- Parcela = 20 + 21 = 41 cuadrículas.
Ejemplo de resolución del trabajo de las parcelas:
Ejemplo de resolución del trabajo sobre la circunferencia:
