3 ESO

Aprender a dibujar el espacio y el volumen (III)

Perspectiva cónica (II)

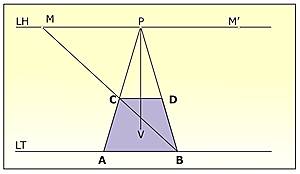	Trazado de la planta del cubo (un cuadrado) en perspectiva cónica frontal

Resolveremos la perspectiva explicando el desarrollo del problema en dos pasos, en los que desarrollaremos las operaciones necesarias.

Paso 1

Situada la distancia entre la línea de tierra y la línea de horizonte en la que señalaremos el punto P, trazaremos a partir de P un segmento perpendicular a la línea de tierra con la distancia P-V y abatiremos esta distancia para hallar los medidores M y M' sobre la línea de tierra.

Una vez hallados estos puntos, hemos de situar la planta del cubo en perspectiva. Para ello, situaremos el segmento A-B en la línea de tierra con la orientación que marca el planteamiento del ejercicio en el sistema diédrico. En este caso, el observador mira desde el centro del cubo. Seguidamente, trazaremos dos rectas que fuguen al punto P desde A y B respectivamente. Por último, para calcular la profundidad del cubo, uniremos el punto B con el medidor M para hallar el punto intersección C. Para completar la planta trazaremos una recta desde C paralela la línea de tierra que originará el punto D. El cuadrado dado en la planta se transformará en un trapecio isósceles debido a la profundidad perspectiva.