Función radical - 1
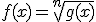 , para n entero
El dominio de la función depende del índice n:
, para n entero
El dominio de la función depende del índice n:
- Si
n es un número par, el dominio es el
intervalo en el que
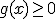 .
<
.
< - Si n es un número impar, el dominio es
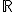 .
.
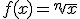 , recuerda que las
raíces se pueden escribir como exponentes fraccionarios,
, recuerda que las
raíces se pueden escribir como exponentes fraccionarios, 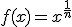 .
Estas
funciones irracionales son funciones
potenciales con exponente fraccionario.
.
Estas
funciones irracionales son funciones
potenciales con exponente fraccionario.
Activa la casilla de “función inversa” para representar la gráfica de la función inversa de la función irracional.
Activa la casilla de verificación para visualizar la función inversa.
La barra de Entrada te permite introducir el valor exacto del índice. Para ello, lo único que debes hacer es escribir el índice igual al número, por ejemplo n=2.
1. Calcula el dominio de las funciones:
a.
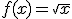
b.
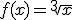
c.
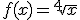
2. La función inversa de una función f(x) es otra función, f-1, tal que para cualquier valor de x de su dominio se cumple que f(x)=b, entonces f-1(b)=x, por lo tanto, sus gráficas será simétricas respecto a la recta y=x.
a. Calcula la función inversa de
, represéntala gráficamente.
b. Calcula la función inversa de
, represéntala gráficamente.
c. Calcula la función inversa de
, para n par. Represéntala gráficamente.
d. Calcula la función inversa de
, para n impar. Represéntala gráficamente.
3. Explica que función se obtiene para n=1. ¿Por qué?

Esta obra está bajo una licencia de Creative Commons.