Función de proporcionalidad inversa. Hipérbola
Enunciado
Las funciones racionales son aquellas funciones que se obtienen de un cociente de polinomios:
,
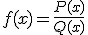siendo el grado de 
Un caso particular es la Función
de proporcionalidad inversa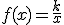 
, con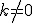 
. Su gráfica es una hipérbola.
Con ayuda de la aplicación estudia las propiedades de las funciones racionales.
Qué hacer
Moviendo el deslizador verde puedes cambiar el valor de la constante de proporcionalidad inversa "k"
Desplaza el punto amarillo, sobre el eje de abcisas, para calcular la imagen de la función para x0.
El número que está dentro del rectángulo naranja representa el área de dicho rectángulo que es la constante de proporcionalidad inversa
Preguntas
1. Representa
gráficamente la función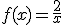 
, calculando la tabla de valores:
|
x |
-10 |
-5 |
-2 |
-1 |
0 |
1 |
2 |
5 |
10 |
|
f(x) |
|
|
|
|
|
|
|
|
|
a. ¿Tiene algún punto de discontinuidad?
b. ¿Corta a los ejes de coordenadas?
c. ¿Tiene asíntotas horizontales? ¿Y verticales?
d. La función es ¿creciente o decreciente?
2. Repite el
ejercicio anterior para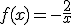 
3. Si A(x0,f(x0)) en un punto de la gráfica de una función de proporcionalidad inversa, sabiendo que el producto de sus coordenadas es 5, es decir que el producto de x0 por f(x0) sea igual a 5 ¿Cuál es la ecuación de la función? Represéntala gráficamente.
4. Averigua la ecuación de una función de proporcionalidad inversa que pasa por el punto A(2,1).
Esta obra está bajo una licencia de Creative Commons.