Proyecto correspondiente a la Práctica IV
El objetivo del proyecto es que edites las páginas Punto-pendiente.htm y Punto-pendiente_2.htm de la carpeta Ejercicios, con las que has trabajado durante las tres primeras prácticas, y que modifiques las escenas que contienen siguiendo las especificaciones siguientes.
Recuerda que si lo deseas puedes acceder a las Actividades Guiadas donde te indicamos las soluciones a cada ejercicio.
Vas a trabajar con las seis escenas de las páginas Punto-pendiente y Punto-pendiente (2). Además de las propuestas que se hacen para cada escena a continuación, en cada una de ellas debes incluir junto al nombre de la escena tus iniciales. Observa en cada caso el contenido del campo codebase y comprueba que si lo cambias no se ve la escena.
Primera escena
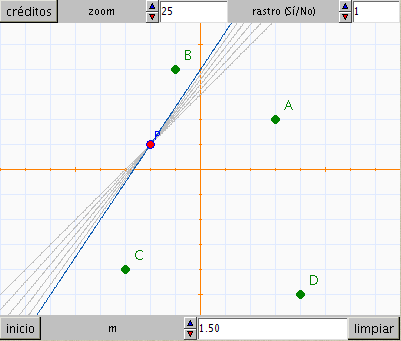
Define un control, que puedes llamar rastro
que permita elegir en la escena si se desea que la recta deje o no
rastro al cambiar la pendiente o la posición del punto.
Segunda escena
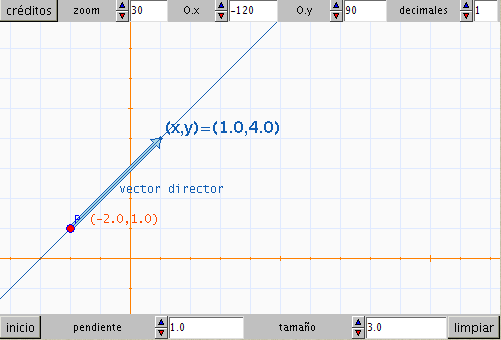
Utiliza la función f que está definida en auxiliares
para escribir la ecuación que representa la recta que pasa por P y
tiene de pendiente m, sustituyendo la ecuación que hay en gráficos
por una que utilice la función f.
Define en el panel de auxiliares una constante que tome el valor de P.x+t, que aparece en varias instrucciones de gráficos, y sustituye la suma P.x+t por esa constante en todas las expresiones donde aparezca.
Define un control d que afecte y permita modificar los decimales de todos los números que aparecen en la escena, coordenadas y controles.
Aumenta el tamaño de la escena para que
quepan bien los nombres de los controles superiores.
Tercera escena
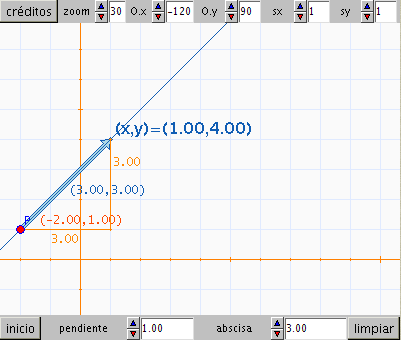
Utiliza de nuevo la función f para escribir en gráficos
la ecuación que representa la recta que pasa por P y tiene de pendiente
m, como en el ejercicio anterior. Usa también la función f para definir
un vector de nombre e, de dos
dimensiones con las coordenadas del punto (x,y),
extremo del vector director.
Usa las componentes del vector e en todas las expresiones que proceda del panel gráficos.
Para evitar que el valor del segmento horizontal se acerque o se aleje al segmento al aumentar o disminuir la escala hazlo proporcional a la escala, define una constante s que indique la separación en cada caso.
Define dos controles sx y sy
que permitan que se dibujen o no los segmentos amarillos.
Cuarta escena
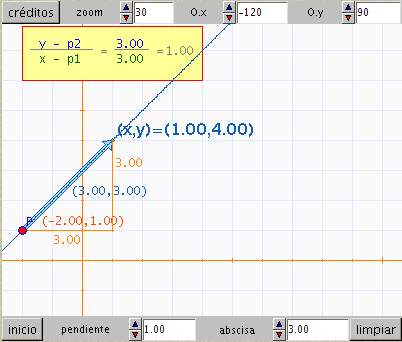
Define las funciones: a(x)=((x*30)-120-Ox)/escala y b(x)=((x*30)-90+Oy)/escala para obtener las coordenadas de los vértices del rectángulo que enmarca el texto de la escena de forma absoluta, es decir, sin que dependan del zoom (escala) ni de la posición de los ejes (Ox y Oy).
Aplica estas funciones a las coordenadas que definen dicho rectángulo en la instrucción polígono del panel de gráficos.
Activa en esta instrucción la casilla fondo para que el rectángulo no se redibuje al usar los pulsadores de los controles numéricos o desplazar el control gráfico.
Como en la escena anterior haz que la posición del valor del
segmento inferior no dependa del zoom.
Quinta escena
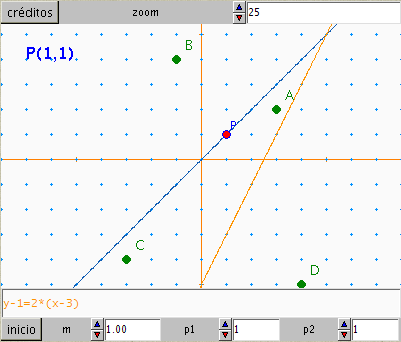
Para conseguir que el control P se mueva sólo por
los puntos de la cuadrícula define en auxiliares
las variables: P.x=ent(P.x) y P.y=ent(P.y),
donde ent es la función parte entera y (P.x,P.y)
son las coordenadas del control gráfico P. Como los
valores de las coordenadas de P son números enteros asigna cero
decimales a todos los valores de las coordenadas que aparecen
en la escena y al incremento de los controles P.x
y P.y asígnales el valor 1.
Define dos constantes w
y h que contengan los valores de ancho
(widht) y alto (height) de la escena. Define
también dos constantes nx y ny
que permitan dibujar la familia de puntos que forman la cuadrícula en
los puntos de coordenadas enteras, sea cual sea el zoom de la escena y
que dependan de los valores de w y h,
para ello modifica la instrucción sucesión en el
panel de gráficos, teniendo en cuenta las
constantes nx y ny. Activa la
casilla fondo de esta instrucción para que la
representación sea más rápida.
Sexta escena
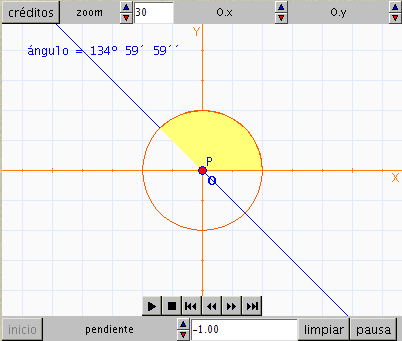
Define la constante pi como 3.14159
y úsala en las expresiones que proceda.
Define una nueva función atg que obtenga, a partir del valor de la tangente, los valores de los ángulos en el intervalo (0,180), en grados sexagesimales; en lugar de la función arco tangente (atan), que los obtiene en el intervalo (-pi,pi) en radianes. Utiliza en la nueva función en lugar de la función atan, para que las representación del arco de color blanco sea correcta también cuando las pendientes son negativas. Utiliza la orden relleno del arco. Elimina las instrucciones del arco azul y de la semirrecta gris.
Sustituye el arco rojo por una circunferencia completa, con centro en el punto P, radio 2 y el color rojo oscuro.
Comprueba que una variable puede actuar como una función si depende de x, por ejemplo, si se define r = m*(x-P.x)+P.y y se escribe la ecuación y=r el valor de r se calcula para cada x y, por lo tanto, se representa la recta correspondiente.
Escribe los nombres de los ejes (X e Y) y del origen de coordenadas (O) junto a los ejes, de forma que se actualice al desplazar los ejes.
Define un algoritmo para determinar el ángulo en grados minutos y segundos, para que se escriba el ángulo de esta manera.
Define una animación que haga variar el
valor de la pendiente para que recorra los valores de -10
a 10.
Las actividades propuestas en este proyecto se corresponden con las desarrolladas en las Actividades Guiadas. Si lo deseas puedes seguir las indicaciones que se dan allí o consultar en la documentación de Descartes alguno de los pasos que no hayas sabido resolver.
Después de finalizar el proyecto puedes pasar a la actividad no guiada y finalmente a la página de Evaluación.





