Proyecto correspondiente a la Práctica III

El objetivo del proyecto es crear una carpeta que debe contener las carpetas y archivos necesarios para poder visualizar escenas de Descartes en cualquier ordenador.

Dicha carpeta deberá contener dos páginas html más la carpeta imágenes comunes. La estructura de carpetas debe permitir la correcta carga de la página con las imágenes en el navegador.

La primera página será punto_pendiente.html, que has editado en las dos primeras prácticas del curso. La segunda se llamará punto_pendiente2.htm.

En la página punto_pendiente.html debes modificar las dos escenas que contiene (Primera escena y Segunda escena) e introducir dos nuevas (Tercera escena y Cuarta escena). La página punto_pendiente2.html debe contener dos escenas (Quinta escena y Sexta escena).

Las modificaciones en las escenas y en el contenido de las dos páginas son las que te indicamos a continuación:

Primera escena

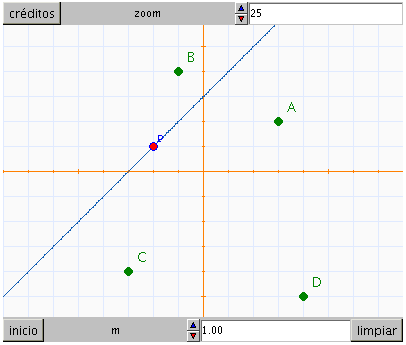
La primera escena debe tener el aspecto de la figura, donde se han añadido los puntos A, B, C y D que se definen con coordenadas constantes. También debes proponer dos nuevas actividades:

2.- Dibuja el haz de rectas paralelas que tienen de pendiente 1, 2 y 1/2.
3.- Dibuja el haz de rectas que pasa por cada uno de los puntos A, B, C y D.

Segunda escena

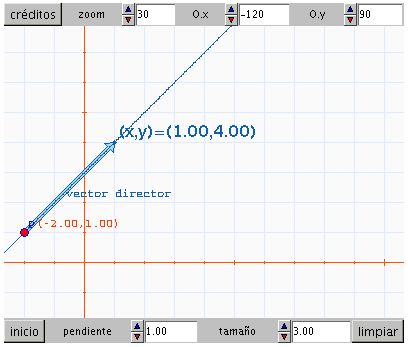
En esta segunda escena los puntos P y (x,y) deben tener colores similares a los que se aprecian en la imagen anterior y al modificar su posición o la pendiente se deben actualizar las coordenadas.

Observa la recta difuminada que pasa por ambos puntos. El control tamaño debe indicar la diferencia de abscisas entre los puntos (x,y) y P, es decir, x=P.x+tamaño.

Tercera escena

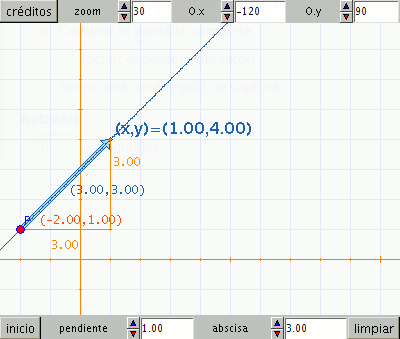
En esta escena, similar a la anterior, debes añadir los segmentos correspondientes a las coordenadas del vector director, sus respectivos valores numéricos junto a cada segmento y las coordenadas del vector junto a él.

Añade también el siguiente enunciado:

Relación entre las coordenadas del vector director y las coordenadas de los puntos P y (x,y)
Las coordenadas del vector director son los números que hay que sumar a las coordenadas del origen para obtener las del extremo.

Y también incluye la siguiente propuesta de trabajo para el alumno:

5.- Comprueba que las coordenadas del extremo menos las del origen dan las coordenadas del vector director, sean cuales sean los puntos y la pendiente que elijas.

Cuarta escena

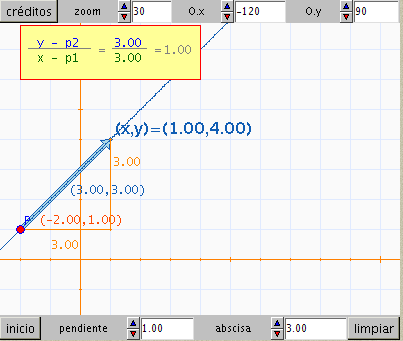
El enunciado de la escena debe ser:

Relación entre cualquier vector director de una recta y su pendiente (m)
El cociente de la ordenada entre la abscisa de cualquier vector director de una recta concreta siempre da el mismo resultado.

Y la propuesta de trabajo:

6.- Observa las coordenadas del vector de dirección e intenta encontrar una relación entre esas coordenadas y la pendiente de la recta. (Elige una pendiente y prueba con distintos puntos de la misma recta. Después comprueba tus hipótesis con diferentes rectas).

Quinta escena

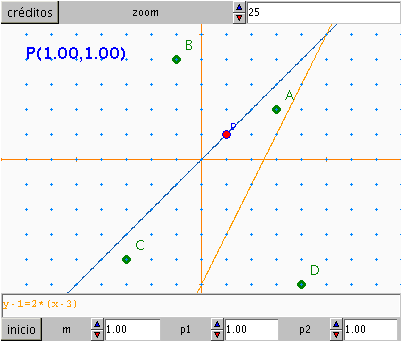
En esta escena debe aparecer difuminada la recta que pasa por P(p1,p2) y tiene la pendiente indicada. Debe haber otra recta que es la que tiene su ecuación en la escena, que ha de ser editable para que el alumnado escriba la ecuación, se escribirán en la parte superior las coordenadas del punto P y en lugar de la cuadrícula habitual se pondrá la cuadrícula de puntos.

El enunciado de esta escena es:

Ecuación de la recta que pasa por P y tiene de pendiente m
En la actividad anterior habrás obtenido que el cociente de la ordenada entre la abscisa de cualquier vector director es precisamente la pendiente de esa recta. Por lo tanto si (p1,p2) son las coordenadas de P, (x,y) es un punto cualquiera de la recta y m su pendiente se verifica que:

Y la propuesta de trabajo:

7.- Escribe la ecuación de la recta de la que se conocen las coordenadas de un punto por donde pasa y su pendiente. (Para cada caso coloca el punto P en la posición que se indica y escribe el valor de la pendiente m, con lo que tendrás la referencia de la recta que se debe representar, luego escribe la ecuación y comprueba si coincide).
a) pasa por A y m=2        b) pasa por A y m=3
c) pasa por B y m=1/2     d) pasa por B y m= -1/2
e) pasa por C y m=12/7   f) pasa por C y m= -2
g) pasa por D y m= -1      h) pasa por D y m=0
prueba con otros puntos y las pendientes que quieras.

Sexta escena

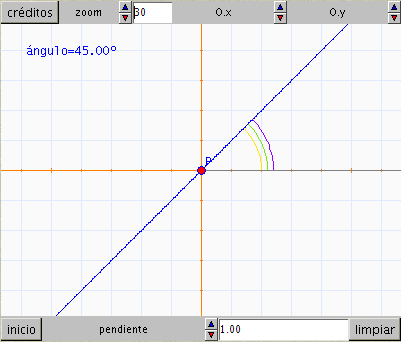
En esta escena el control debe moverse por el eje de abscisas y cada uno de los arcos indicados en la figura debe representarse usando un método distinto, dos de ellos con la herramienta arco, usando las dos posibilidades que esta herramienta ofrece, y el tercero usando la herramienta curva.

Con el enunciado:

Relación entre el ángulo de una recta y su pendiente
Se llama ángulo de una recta al que forma esa recta y el semieje OX positivo.

Y la propuesta de trabajo:

8.- Observa el ángulo que forma cada recta, cuando se cambia la pendiente.

Las actividades propuestas en este proyecto se corresponden con las desarrolladas en las Actividades Guiadas. Si lo deseas puedes seguir las indicaciones que se dan allí o consultar en la documentación de Descartes alguno de los pasos que no hayas sabido resolver.

Después de finalizar el proyecto, realiza la actividad no guiada y puedes pasar a la página de Evaluación.