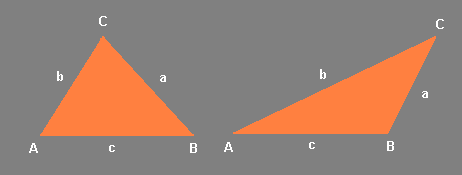

Resolución de triángulos oblicuángulos
INTRODUCCIÓN.
Esta unidad didáctica pretende que el alumno se familiarice con los distintos casos de resolución y llegue a adquirir la habilidad para saber de antemano si el problema va a tener o no solución y cuantas soluciones puede encontrar.La posibilidad de manipulación de los elementos hasta llegar a la construcción del triángulo facilitará la comprensión de las propiedades que han de cumplir los elementos de un triángulo cualquiera.
Un triángulo que no es rectángulo se le llama oblicuángulo(*). Los elementos de un triángulo oblicuángulo son los tres ángulos A, B y C y los tres lados respectivos, opuestos a los anteriores, a, b y c.

Un problema de resolución de triángulos oblicuángulos consiste en hallar tres de sus elementos, lados o ángulos, cuando se conocen los otros tres (uno de los cuales ha de ser un lado).
(*) Oblicuángulo se contrapone a rectángulo, en sentido estricto. Pero cuando se habla de triángulos oblicuángulos no se pretende excluir al triángulo rectángulo en el estudio, que queda asumido como caso particular. No obstante cuando el triángulo es rectángulo, porque se dice expresamente que lo es, el problema se reduce, tiene un tratamiento particular y no se aplican las técnicas generales de resolución que vamos a ver seguidamente.
Se utilizan tres propiedades:
| Suma de los ángulos de un triángulo |
A + B + C = 180º |
| Teorema del seno | 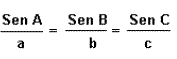 |
| Teorema del coseno | a2 = b2
+ c2 - 2·b·c·Cos A
b2 = a2 + c2 - 2·a·c·Cos B c2 = a2 + b2 - 2·a·b·Cos C |
Casos en la resolución de triángulos:
| CASO | DATOS CONOCIDOS | INCÓGNITAS |
| I | Los tres lados: a, b, c | Los tres ángulos A, B, C |
| II | Un lado y los ángulos adyacentes:a, B, C | Dos lados y un ángulo: b, c, A |
| III | Dos lados y el ángulo formado: a, b, C | Un lado y dos ángulos: c, A, B |
| IV | Dos lados y el ángulo opuesto a uno de ellos: a, b, A | Un lado y dos ángulos: c, B, C |
Seleccionar un caso...
Autor: Ángel Cabezudo Bueno
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||