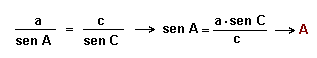 |
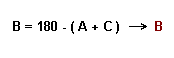 |

Resolución de triángulos oblicuángulos
ORIENTACIONES
Los lados conocidos a y b tienen el extremo común C.
Ahora se puede dar cualquier valor a los lados a y b. La única limitación la impone el ángulo C que forman (C < 180º).
Desde el punto de vista constructivo, este caso no requiere más que unir los extremos libres de los lados a y b.
Inicialmente la escena presenta los valores a = 6, b=8 y C=100º.
La solución trigonométrica se consigue aplicando en el mismo orden las siguientes propiedades:
1º Teorema del coseno para calcular el lado c,
2º Teorema del seno para calcular el ángulo A
3º Una vez conocidos A y C, la propiedad de la suma de los tres ángulos para calcular B.
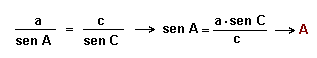 |
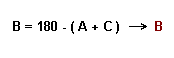 |
ACTIVIDADES
NOTA 1: El extremo A contiene un punto de control que se desplaza sobre la recta que une los vértices A y B.
Cada vez que se cambien los parámetros b y C, que alteran la posición del punto A, habrá que corregir la posición del control y llevarlo a la nueva posición de A para poder realizar el nuevo trazado del lado c
11.- Con los valores iniciales a = 6, b = 8 y C =100. Construye el triángulo dibujando el segmento b que une el extremo A con el extremo B. Para ello 'pincha' con el botón izquierdo del ratón sobre A y arrastra hasta B. Dibuja el triángulo en tu cuaderno partiendo de los datos que te dan.
12.- Aplica las fórmulas trigonométricas para solucionar el triángulo y comprueba la solución dada por el programa. Escribe los cálculos que haces en el cuaderno.
13.- Pulsa el botón Inicio y cambia el ángulo C a 180º. Desplaza el control a la posición del punto A. Dibuja el segmento AB. Lee e interpreta la solución sobre la pizarra. ¿ Porqué los ángulos A y B miden 0º ? ¿ Se cumple la propiedad triangular entre los lados a, b y c ?.
Autor: Ángel Cabezudo Bueno
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||