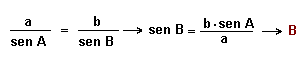 |
 |
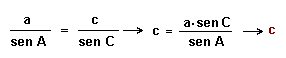 |

Resolución de triángulos oblicuángulos
ORIENTACIONES
Este caso es el más complejo ya que se pueden dar tres situaciones:
No existe triángulo
Existe un triángulo
Existen dos triángulos.
Suponemos conocidos los lados a y b y el ángulo A opuesto al lado a.
La solución trigonométrica se consigue aplicando las siguientes propiedades en el mismo orden:
1º Teorema del seno para calcular el ángulo B
2º La propiedad de la suma de los tres ángulos para calcular C
3º Nuevamente el Teorema del seno para calcular el lado c
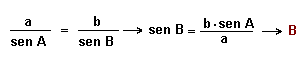 |
 |
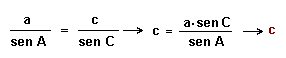 |
El siguiente cuadro resume los posibles casos que pueden darse y que el alumno podrá comprobar en las actividades que se proponen más adelante. No es necesario memorizarlo, simplemente hágase una idea de las posibilidades que se tiene:
|
h = b.sen A > a |
ninguna solución | ||
| h = b.sen A = a | A < 90º | una solución | |
| A >= 90º | ninguna solución | ||
| h = b.sen A < a | a > b | una solución | |
| a = b | A < 90º | una solución | |
| A >= 90º | ninguna solución | ||
| a < b | A < 90º | dos soluciones | |
| A >= 90º | ninguna solución | ||
ACTIVIDADES
NOTA 1: El lado a es un segmento unido por un extremo al lado b y que podemos girar libremente pinchando el extremo B del mismo y arrastrando ya representa este un control.
NOTA 2: La distancia h=b.sen A entre el vértice C y la recta AH es determinante para que se pueda o no formar el triángulo.
14.- Comprobar que inicialmente a = 8, b = 5, A = 60º . Girar el extremo B hasta incidir con la recta AH y compruebe que existe un único punto de corte y por lo tanto existe un triángulo como solución.
15.- Trata de sobreponer a en h ¿ qué relación hay entre a y h ?. Trata de sobreponer a en b ¿qué relación hay entre a y b?. Consultar después la tabla orientativa anterior y verificar las respuestas que hayas dado.
16.- Fíjate en la longitud que tiene h y disminuye la longitud del lado a hasta hacer que h > a. Desplaza el control de B, para que la longitud de a se adapte a la nueva situación. ¿ Se forma triángulo ?. Consulta la tabla orientativa anterior y verifica la respuesta.
17.- Comprueba el caso en que a > h, a < b y A < 90º. Para ello pulsa el botón de inicio y escribe b = 9. Gira el control para que corte el lado a a la recta AH. ¿ Cuántos puntos de corte se obtienen ? ¿ Cuántos triángulos se pueden construir ?. Consulta la tabla orientativa y verifica la respuesta.
18.- Comprueba que cuando hay dos triángulos, los dos ángulos B posibles son suplementarios (B + B' = 180º)
19.- ¿ Qué pasaría si en el supuesto anterior haces que A >=90º ?. Consulta la tabla orientativa y verifica la respuesta.
20.- Escribe a, b, A para cada caso de la tabla orientativa y comprueba la solución.
21.- Observa que para que se pueda construir el triángulo es necesario que sen B = h / a < = 1 ( h = b . sen A < = a) y que A + B < 180º
22.- Resuelve los siguientes triángulos, haciendo los cálculos y dibujando la construcción en tu cuaderno. Para ello usa una calculadora científica (como siempre, puedes valerte de la calculadora de Windows) y emplea las fórmulas dadas en las orientaciones anteriores.
a = 3, b = 5, A = 80º
a = 6, b = 5, A = 36,5º
a = 5, b = 6, A = 36,5º
NOTA 3: Cuando un problema tenga dos soluciones, el ángulo B' del segundo triángulo es suplementario del ángulo B del primero, B' = 180º - B
Autor: Ángel Cabezudo Bueno
| Ministerio de Educación, Cultura y Deporte. Año 2000 | ||