Propiedades de la función exponencial

	PROPIEDADES DE LA FUNCIÓN EXPONENCIAL
	4º ESO Opción B

Las actividades a realizar han de combinar el cuaderno de trabajo con el ordenador y/o con la calculadora:

Recordemos que se llamaban funciones exponenciales a las funciones de la forma f(x) = a^x o y = a^x, donde la base de la potencia "a" es constante (un número positivo) y el exponente la variable x.

ACTIVIDAD 8 ESTUDIO DE LA FUNCIÓN

a) Completa la siguiente tabla de valores correspondiente a la función f(x) =2

x	-2	-1,5	-1	-0,5	0	0,5	1	1.4	2	2,6

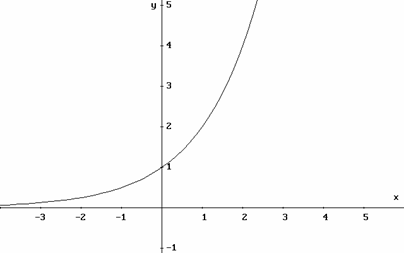Su representación gráfica es la siguiente:

b) ¿Existe algún punto donde esta función no

esté definida? ¿Cuál es su DOMINIO?

c) ¿Para algún valor de la abscisa, la ordenada es

negativa? ¿Por qué?

d) ¿Cuál es el RECORRIDO de esta función?

e) ¿Es creciente o decreciente? ¿Por qué? f) ¿Es una función CONTINUA? ¿Por qué

1.- Observa que en la función representada para valores grandes de x es preciso usar el "zoom" de la escena.

2.-Observa los valores que va tomando "y" a medida que x crece .

3.-Observa los valores que va tomando "y" a medida que x decrece .

Siempre, si se desean ver más valores en la pantalla, se puede reducir la escala, señalando sobre la flecha roja del botón "zoom", o mover los ejes señalando sobre los botones superiores 0.x , 0.y

1.- Observa la siguiente escena que representa la función exponencial

y = a^x. Inicialmente el valor de a es 2.

2.-Observa los valores que va tomando "y" si se van variando los de x.

3.-Haz lo mismo con los valores de "a" a=3, a=4 ,.... a>1

¿qué se va observando en la gráfica dibujada en azul?.

ACTIVIDAD 9 QUE FUNCIÓN DECRECE MÁS

Estudiaremos ahora algunas funciones exponenciales de base menor que la unidad: f(x) = (1/2) y g(x) = (1/3)

a) Completa, como en los casos anteriores, las correspondientes tablas de valores:

x

-2

-1,5

-1

-0,5

0

0,5

1

1.4

2

2,6

(1/2)

(1/3)

b) Representa gráficamente ambas funciones. c) ¿Cuál es su dominio? ¿Y su recorrido?

d) ¿Son crecientes o decrecientes? ¿Por qué? e) Estudia su continuidad.

f) ¿Cuál de las dos funciones decrece más rápidamente? ¿Por qué?

1.- Observa que en las funciones representadas para valores grandes de x es preciso usar el "zoom" de la escena.

2.-Observa los valores que va tomando "y" a medida que x crece .

3.-Observa los valores que va tomando "y" a medida que x decrece .

1.- Observa la siguiente escena que representa la función exponencial
y = a^x. Inicialmente el valor de a es 2.

2.-Observa los valores que va tomando "y" si se van variando los de x (cambiarlos en la ventana inferior correspondiente).

3.-Haz lo mismo con los valores de "a" ¿qué se va observando en la gráfica dibujada en azul?.

4.-En particular, ¿qué se observa cuando a = 1, a >1, a <1 pero siempre a positivo?.

5.-¿Y en el caso en que sea a negativo?.Observa que si a = 0, se trata de la función 0, sin interés.

De las observaciones anteriores deducimos las propiedades de las funciones exponenciales: ¿Podrias enumerarlas?

ACTIVIDAD 10 EL CRECIMIENTO DE INTERNET

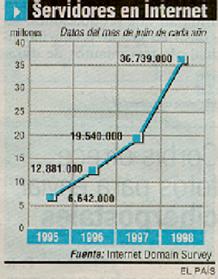
"¿ LA RED INTERNET TIENE UN CRECIMIENTO EXPONENCIAL ?"

El número de servidores conectados a Internet casi se ha duplicado en el último año

y ha llegado en julio de 1998 a más de 36 millones, cuando en las mismas fechas del

año pasado se situaba en 19 millones de servidores.

A partir de la gráfica, confecciona una tabla:

Años

Nº de servidores

¿El ritmo de crecimiento podría ajustarse a un modelo exponencial?.Razonarlo

Miguel Ángel Cabrerizo Romero

Ministerio de Educación, Cultura y Deporte. Año 2005

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.

	Miguel Ángel Cabrerizo Romero

	Ministerio de Educación, Cultura y Deporte. Año 2005