CADENAS DE MARKOV

CADENAS DE MARKOV-IV

(Es conveniente repasar la resolución de sistemas)

VECTOR FIJO DE UNA MATRIZ DE TRANSICIÓN REGULAR

Se llama vector fijo de probabilidad de la matriz regular P de orden 2, al vector de probabilidad

tal que verifica:

Es decir que tiene que cumplir:

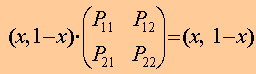
sus coordenadas se obtienen resolviendo la ecuación lineal en la variable x correspondiente, tras hacer el producto de matrices. O bien utilizando la escena siguiente:

1º)Calcula el punto fijo de las matrices regulares de orden 2
de los apartados anteriores. Por ejemplo para la matriz

resulta el vector fijo: (1/3,2/3)

Comprueba con las potencias de P que dicha cadena

es regular, pues para cadenas no regulares no hay punto fijo.

Una vez calculado el vector fijo:

Observa qué vector aparece en las sucesivas potencias de P como vectores fila de esa potencia.

Se llama vector fijo de probabilidad de la matriz regular P de orden 3, al vector de probabilidad

tal que verifica:



   Es decir que tiene que cumplir:

Sus coordenadas se obtienen resolviendo la ecuación lineal en la variable x
correspondiente, tras hacer el producto de matrices. O bien utilizando la escena siguiente:

2º)Calcula el punto fijo de las matrices regulares de orden 2
de los apartados anteriores. Por ejemplo para la matriz

Comprueba con las potencias de P que dicha cadena
es regular, pues para cadenas no regulares no hay punto fijo.
Una vez calculado el vector fijo observa qué vector aparece en las
sucesivas potencias de P como vectores fila de esa potencia.

Resuelve los ejercicios del Boletín de clase, utilizando las escenas y alguno sin utilizarlas para comparar resultados.

1º).                      Un psicólogo hace los supuestos siguientes que conciernen al comportamiento de ratas sujetas a un régimen especial de alimentación. Para una prueba particular, 80% de las ratas que fueron para la derecha en el experimento previo hicieron lo mismo en esta prueba, y 60% de aquellas que fueron para la izquierda en el experimento previo, fueron para la derecha en esta prueba. Si 50% van a la derecha en la primera prueba, ¿qué se podría predecir para la milésima prueba?.

2º) Un ascensor de un edificio con bajo y dos pisos realiza viajes de uno a otro piso (lleno o vacío de ocupantes). El piso en el que termina el viaje n-ésimo del ascensor sigue una cadena de Markov. Se sabe que la mitad de los viajes que parten del bajo se dirigen a cada uno de los otros dos pisos , mientras que si un viaje comienza en el primer piso, sólo el 25 5 de las veces finaliza en el segundo. Por último, si un trayecto comienza en el segundo piso, siempre termina en el bajo.

¿Cuál es la probabilidad de que, a largo plazo, el ascensor se encuentre en cada uno de los tres pisos?.

DISTRIBUCIÓN ESTACIONARIA

Cuando la matriz de transición P de un proceso de Markov es regular, observamos que conforme aumentan las potencias de P, los vectores fila de esas matrices se estabilizan en unos valores determinados hasta coincidir todas las filas y esos valores son precisamente los componentes del vector fijo de P.

Entonces

Teorema:

Consideremos una cadena de Markov regular. La probabilidad de que un estado ai suceda después de un número grande de pruebas es igual a la componente i-ésima del vector fijo asociado.

Por tanto las probabilidades absolutas (DISTRIBUCIÓN ESTACIONARIA DE LA CADENA DE MARKOV) de que ocurra un determinado estado son independientes de las condiciones iniciales del sistema.

Resuelve los siguientes ejercicios:

4º) Una persona sabe que si un día tiene indigestión está un 70% seguro de que no la tendrá al día siguiente, pero si un día no tiene indigestión, tiene un 60% de probabilidad de tampoco tenerla al día siguiente. a lo largo de los años, ¿con qué frecuencia estará con indigestión?
Si calculas el vector fijo y las sucesivas potencias de P obtendrás que, aproximadamente el 36% de los días la persona estará con indigestión.

5º)La región de ventas de un vendedor la componen tres ciudades A, B y C. Nunca vende en la misma ciudad en días seguidos. Si vende en la ciudad A, entonces al día siguiente vende en la ciudad B. Sin embargo, si vende en una de las dos B o C, entonces al día siguiente está en doble posibilidad tanto para vender en A como en la otra ciudad . A la larga con qué frecuencia (en %) vende en cada ciudad?

Sol.:   40% en A, 45% en B y 15% en C
6º) Un agente comercial realiza su trabajo en tres ciudades gallegas: La Coruña, Ferrol y Santiago. Para evitar desplazamientos innecesarios está todo el día en la misma ciudad y duerme en ella, desplazándose a otra al día siguiente, si no tiene suficiente trabajo. Después de estar trabajando un día en La Coruña, la probabilidad de tener que seguir trabajando en ella al día siguiente es de 0.4, la de tener que viajar a Santiago es 0.4y la de tener que ir a Ferrol es de 0.2. si el viajante duerme un día en Santiago, con probabilidad del 20% tendrá que seguir trabajando en la misma ciudad al día siguiente, en el 60% de los casos viajará a La Coruña, mientras que irá a Ferrol con probabilidad 0.2. Por último, si el agente comercial trabaja todo un día en Ferrol, permanecerá en al misma ciudad , al día siguiente, con una probabilidad de 0.1, irá a Santiago con una probabilidad de 0.3 y a La Coruña con probabilidad 0.6.
¿Cuáles son los porcentajes de días en los que el agente comercial está en cada una de las tres ciudades?.

7º)Un estudio de audiencia demuestra que si una persona ve cierto culebrón de televisión una tarde está un 30% segura de que también lo verá a la tarde siguiente, pero se non lo ve una tarde hay un 60% de posibilidades de que no lo vea tampoco a la tarde siguiente. ¿Qué frecuencia de audiencia tendrá el culebrón?



María Blanca Gómez Rodríguez

Ministerio Educación. Año 2005


	1º)Calcula el punto fijo de las matrices regulares de orden 2 de los apartados anteriores. Por ejemplo para la matriz resulta el vector fijo: (1/3,2/3) Comprueba con las potencias de P que dicha cadena es regular, pues para cadenas no regulares no hay punto fijo. Una vez calculado el vector fijo: Observa qué vector aparece en las sucesivas potencias de P como vectores fila de esa potencia.

Se llama vector fijo de probabilidad de la matriz regular P de orden 3, al vector de probabilidad tal que verifica: Es decir que tiene que cumplir: Sus coordenadas se obtienen resolviendo la ecuación lineal en la variable x correspondiente, tras hacer el producto de matrices. O bien utilizando la escena siguiente:

	2º)Calcula el punto fijo de las matrices regulares de orden 2 de los apartados anteriores. Por ejemplo para la matriz Comprueba con las potencias de P que dicha cadena es regular, pues para cadenas no regulares no hay punto fijo. Una vez calculado el vector fijo observa qué vector aparece en las sucesivas potencias de P como vectores fila de esa potencia.

	María Blanca Gómez Rodríguez

	Ministerio Educación. Año 2005