BOLETÍN DE MARKOV

1º)La ilustración

Muestra un anuncio luminoso. Las letras que lo forman se encienden alternativamente según la siguiente regla: La iluminación de una letra se mueve a la derecha con probabilidad 1/3 y hacia la izquierda con probabilidad 2/3. Cuando está encendida una de las letras de los extremos en el paso siguiente se ilumina  la letra central adyacente. Calcular la probabilidad de que si está iluminada la letra G, se ilumine la letra I después de tres pasos.

Calcular la distribución de probabilidades absolutas después de cuatro pasos.

2º).             Dadas las siguientes matrices, estúdiese si son matrices de transición regulares.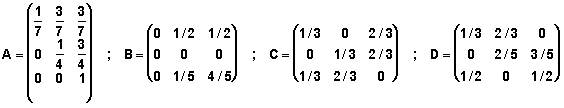
Calcular los puntos fijos de las matrices regulares. Compruébese el teorema 3  con las matrices regulares.

3º).             Una persona tiene constatado que si un día está resfriado está un 70% seguro de que no lo estará al día siguiente, pero si un cierto día no está resfriado tiene un 60% de probabilidad de no estar tampoco al día siguiente.  A lo largo de los años, ¿con qué frecuencia estará resfriado?.

4º).             Encontrar las distribuciones estacionarias correspondientes a las cadenas de Markov con las matrices de transición siguientes:

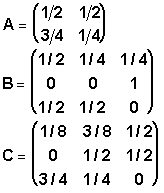
5º).             Un estudiante va al instituto andando o en autobús. Cuando va andando un día, la probabilidad de que al día siguiente coja el autobús es 0’6. La probabilidad de que vaya en autobús dos días seguidos es 0’7.¿Aproximadamente con qué frecuencia coge el autobús a lo largo de todo el curso?

 6º).             Escríbanse las siguientes matrices en forma canónica. Cuéntense los estados absorbentes y transitorios en cada caso y compruébese la división en submatrices del ejemplo anterior.

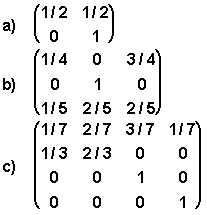
7º).             Los hábitos de estudio de un estudiante son como sigue: Si estudia una noche, está 70% seguro de no estudiar la noche siguiente. Por otra parte, si no estudia una noche , está 60% seguro de no estudiar tampoco la noche siguiente. ¿Con qué frecuencia estudiará a la larga?.

 8º).             Dada la matriz de transición  con distribución de probabilidad P⁽⁰⁾=(1/3   2/3). Definir y hallar

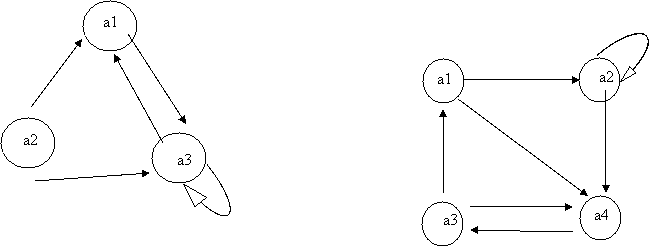
 9º).             Halla la matriz de transición de los siguientes diagramas:

 10º).         Un supermercado realiza la experiencia siguiente en relación con  las preferencias de sus clientes. Se observa que:

El 80% de las personas que compran un día el producto A repite al día siguiente. El 60% de los que no lo  compran el producto A un día, lo compran al día siguiente. Si el 50% compró el producto un día determinado, ¿qué po­demos predecir para la compra del producto el segundo día? ¿Y para el tercero? ¿Y para el milésimo?.

11º).         En una ciudad existen dos partidos políticos, uno de derechas y otro de izquierdas. Los alcaldes son elegidos por un período de un año y se ha observado que la probabilidad de que a un alcalde de derechas suceda otro del mismo signo político es 3/5 y  que a un alcalde de izquierdas siga otro de izquierdas es 1/2. Supo­ngamos que en 1995 hay alcalde de izquierdas. ¿Cuál será la probabilidad de que en 1998 siga un alcalde de izquierdas al frente del concejo ? ¿Que ocurrirá en el año 2000?

 12º).         Una familia planifica cada año sus vacaciones de la siguiente manera. Si un ano va a la montaña al año siguiente va al mar y al segundo año descansa en la casa. Pero al año siguiente es igualmente probable que se traslade al mar o a la montaña. En 1995 quedarán en casa. ¿Dónde es más probable que pasen sus vacaciones en el año 2000? A la  larga, ¿con que frecuencia pasarán las vacaciones en el mar?

13º). 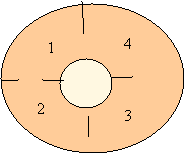        En el diagrama siguiente aparece un laberinto en el que es posible atravesar cada una de las puertas con igual probabilidad.

Una persona situada inicialmente en el  compartimento 1 se mueve de uno a otro sin interrupción. Escríbase la matriz de transición de la cadena de Markov correspondiente y calcúlese la probabilidad de que después de 4 pasos esté en el  compartimento número 3.

 14º).         Un ascensor de un edificio con bajo y dos pisos realiza viajes de uno a otro piso (lleno o vacío de ocupantes). El piso en el que termina el viaje n-ésimo del ascensor sigue una cadena de Markov. Se sabe que la mitad de los viajes que parten del bajo se dirigen a cada uno de los otros dos pisos , mientras que si un viaje comienza en el primer piso, sólo el 25 5 de las veces finaliza en el segundo. Por último, si un trayecto comienza en el segundo piso, siempre termina en el bajo.

A)     Calcular la matriz de probabilidades de transición de la cadena.

B)     Dibujar su gráfico asociado.

C)    ¿Cuál es la probabilidad de que, a largo plazo, el ascensor se encuentre en cada uno de los tres pisos?.

15º).         Un agente comercial realiza su trabajo en tres ciudades gallegas: La Coruña, Ferrol y Santiago. Para evitar desplazamientos innecesarios está todo el día en la misma ciudad y duerme en ella, desplazándose a otra al día siguiente, si no tiene suficiente trabajo. Después de estar trabajando un día en La Coruña, la probabilidad de tener que seguir trabajando en ella al día siguiente es de 0.4, la de tener que viajar a Santiago es 0.4y la de tener que ir a Ferrol es de 0.2. si el viajante duerme un día en Santiago, con probabilidad del 20% tendrá que seguir trabajando en la misma ciudad al día siguiente, en el 60% de los casos viajará a La Coruña, mientras que irá a Ferrol con probabilidad 0.2. Por último, si el agente comercial trabaja todo un día en Ferrol, permanecerá en al misma ciudad , al día siguiente, con una probabilidad de 0.1, irá a Santiago con una probabilidad de 0.3 y a La Coruña con probabilidad 0.6.

a)      ¿Se puede describir la ciudad en la que está cada día el agente comercial mediante una cadena de Markov?.

b)      Si hoy el viajante está en La Coruña, ¿cuál es la probabilidad de que también tenga que trabajar en La Coruña dentro de cuatro días?

c)      ¿Cuáles son los porcentajes de días en los que el agente comercial está en cada una de las tres ciudades?.

 16º).                     En un Instituto hay dos fotocopiadoras iguales, que inicialmente se supone que están en funcionamiento. A lo largo de un día, cada fotocopiadora se avería con una probabilidad de ¼. Al final de la jornada laboral se da parte de las averías producidas a la empresa de mantenimiento que las repara en 24 horas (pero no antes).

a)      ¿Cuál es la distribución del número de fotocopiadoras que están en servicio en el cuarto día?.

b)      ¿Cuál es el porcentaje de los días en los que el Instituto no tiene ninguna fotocopiadora disponible?.

c)      ¿Cuál es el número medio de fotocopiadoras operativas al principio de cada día a alargo plazo?.

17º).                     Un jugador tiene 3.000 euros. Apuesta en cada jugada 1.000 euros con probabilidad de ganar 1/2. El juego ter­mina cuando queda sin dinero o dobla la cantidad inicial. Calcúlese:

a)  Probabilidad de estar a cero después de 5 jugadas.

b)  Probabilidad de que el juego dure más de 7 jugadas.

c)  El número medio de apuestas que hará en el  juego.

d)  ¿Qué es más probable, que pierda todo o doble el dinero?

18º).                     Una urna A contiene 2 bolas blancas y otra B 3 bolas negras. Escogemos al azar una bola de cada urna y las  depositamos en la  otra. Consideremos el número de bolas negras en la urna A para cada paso del experi­mento. Calcúlese la matriz de transición. ¿Cuál es la probabilidad de que la urna A contenga 2 bolas negras después de tres pasos? Si repetimos la prueba un número grande de veces, ¿ cuál es la probabilidad de que halla 2 bolas negras en la urna A?

 19º).                     .Si Jorge encesta, a continuación lo hace Pepe, pero cuando encesta Pepe, Jorge tienen el doble de proba­bilidades que Pepe de encestar a continuación. ¿Quién tiene mejor promedio?

 20º).                     Supongamos dos ruletas con seis números cada una de ellas. La ruleta A tiene 4 números pares y 2 impares y la ruleta B, 1 número par y 5 impares. Echamos al aire una moneda corriente; si sale cara hacemos girar la ru­leta 1 y si sale cruz la número 2. Si aparece número par volvemos a girar la ruleta número 1 y si sale impar la número 2. El proceso se repite indefinidamente. Calcúlese:

 a) La probabilidad de que en el  segundo ensayo hagamos girar la ruleta número 2.

b) La probabilidad de que aparezca número par en el  cuarto ensayo.

c) La frecuencia con que aparecerá número impar tras muchos ensayos.

d) Supongamos que la moneda que echamos inicialmente está trucada de manera que no conocemos las pro­babilidades de sacar cara y cruz. Estímese la frecuencia con que a la  larga saldrá número par.

 21º).                     Una cadena de interruptores eléctricos es tal que la probabilidad de que un interruptor esté abierto é 2/5 si el interruptor precedente también está abierto y  1/3 si el interruptor precedente está cerrado. Si abrimos o cerramos el primer interruptor de la cadena al azar, calcúlese la probabilidad de que el cuarto interruptor esté abierto.

 22º).                     Consideremos los seis vértices de un hexágono regular. Un individuo se mueve continuamente de un vértice a otro con probabilidad 1/4 de trasladarse a un vértice vecino y probabilidad 1/2 de ir al vértice opuesto. Escríbase la matriz de transición de este proceso, estúdiese si es regular y, en caso afirmativo, hállese la distri­bución estacionaria.

	María Blanca Gómez Rodríguez
	Ministerio de Educación, Cultura y Deporte. Año 2005