

CADENAS DE MARKOV-III
| CADENAS DE MARKOV REGULARES |
Son aquellas en las que es posible pasar a través de todos los estados de la cadena sin que este paso se realice de una forma cíclica. A su correspondiente matriz de transición se le denomina MATRIZ DE TRANSICIÓN REGULAR.
Se prueba que una matriz estocástica es regular si todos los elementos de una potencia Pn son positivos, para un cierto valor de n. Todos los estados son transitorios.
Si una matriz tiene un 1 en la diagonal principal, NO es regular (el estado al que corresponde se dirá estado absorbente)
Comprueba con las siguientes escenas
que las matrices M y H son regulares y que las R y
S no son regulares. Observa el diagrama , los 1 en la diagonal principal y
las potencias de P.
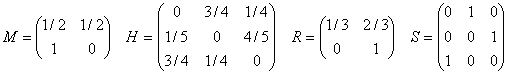
|
1º)Utilizando la escena anterior decir cuáles de las siguientes matrices son regulares y cuáles no. Apunta en tu cuaderno los resultados con las aclaraciones que consideres oportunas a cada caso. 2º)Observa , para n grande, cómo son las filas de las matrices regulares y de las no regulares. Interpreta este resultado.
|
|
|
|
1º)Utilizando la escena anterior decir cuáles de las siguientes matrices son regulares y cuáles no. Apunta en tu cuaderno los resultados con las aclaraciones que consideres oportunas a cada caso. 2º)Observa , para n grande, cómo son las filas de las matrices regulares y de las no regulares. Interpreta este resultado.
|
|
|