

CADENAS DE MARKOV-V
| CADENAS ABSORBENTES. |
Los estados que pueden sucederse a sí mismos y, además, es posible alcanzar, por lo menos, alguno de los restantes desde ellos se llaman estados transitorios.
Un estado tal que si el proceso entra en él permanecerá indefinidamente en este estado (ya que las probabilidades de pasar a cualquiera de los otros son cero), se dice estado absorbente.
De una cadena de Markov que consta de estados transitorios y absorbentes se dice que es una cadena absorbente de Markov.
Si una cadena de Markov contiene algún estado absorbente, la línea de la matriz de transición correspondiente a las probabilidades de transición de dicho estado constará de un 1 en la diagonal principal y ceros en los demás elementos. Será por lo tanto una matriz no regular.
Para poder estudiar las cadenas de Markov absorbentes es preciso reordenar la matriz de transición de forma que las filas correspondientes a los estados absorbentes aparezcan en primer lugar. Así ordenada se dirá que la matriz de transición está en la forma canónica.
Podemos dividir la matriz en forma canónica en cuatro submatrices. La primera es la matriz unidad I, del orden correspondiente. La segunda , la matriz nula. La tercera contiene las probabilidades de paso de estados transitorios a estados absorbentes. La cuarta contiene las probabilidades de estados transitorios a estados transitorios.
Generalizando:
Una cadena de Markov absorbente contiene p estados transitorios y q estados absorbentes. La matriz canónica del proceso presentará el aspecto siguiente:
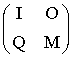
I: matriz identidad de dimensión q
O: matriz nula de dimensión qxp
Q: matriz de dimensión pxq que contiene las probabilidades de paso de estados transitorios a absorbentes.
M: matriz pxp con las probabilidades de los estados transitorios a estados transitorios.
Se llama matriz fundamental de la cadena a la matriz resultado de la operación:
F=(I-M)-1
|
1º)Escribe en la forma canónica las siguientes matrices , indicando el o los
estados absorbentes y los transitorios. Observa el diagrama correspondiente
y ayúdate de las escenas siguientes realizadas para matrices de orden 3
|
|
| Hay un caso más semejante al 4º y al 5º y un caso sin transiciones. Piénsalo. | |
Teorema 5.
Se verifica:
1º). Supongamos que la cadena comienza en un estado transitorio ai. La probabilidad de que llegue a un estado absorbente aj , vienen dada por el elemento de la fila i y la columna j de la matriz F.Q.
2º). La suma de los elementos de la fila i de la matriz F nos proporciona la media del número de veces que la cadena se mueve por estados transitorios antes de caer en un estado absorbente si empieza en el estado transitorio ai.
3º). El elemento fij de la matriz F representa la media del número de veces que la cadena está en el estado transitorio aj, sabiendo que comenzó en el estado transitorio ai, antes de caer en un estado absorbente.
| 2º)Contesta
a cada una de las siguientes preguntas la primera matriz del
ejercicio1º) que has puesto antes en la forma canónica: a) Si el proceso empieza en el estado a1 , ¿cuántos pasos por término medio necesitamos para alcanzar el estado a3? b) Si el proceso empieza en el estado a1 , ¿cuántos pasos por término medio necesitamos para volver al mismo estado? c) Si el proceso empieza en el estado a1 , ¿cuántos pasos por término medio se precisan para caer en uno de los estados absorbentes? d) ¿En qué estado debemos comenzar el proceso para que tarde más en ser absorbido.? e) Si el estado comienza en el estado a1, ¿será más probable que sea absorbido por el a2 o por el a3, en el caso de ser ambos absorbentes?.(matriz tercera) f) ¿Qué estado precisa más pasos del proceso por término medio antes de regresar otra vez a sí mismo? 3º)Dos jugadores A y B tienen dos billetes cada uno. Juegan con una moneda a "cara y cruz" apostando un billete en cada lanzamiento hasta que uno de ellos se arruina. Calcular la probabilidad de que A gane después de 4 jugadas y el número medio de lanzamientos .(antes de caer en estado absorbente (4), si se comenzó en el estado 2). SOLUCIÓN Variable :nº de billetes de A. Espacio de estados E={ 0, 1, 2, 3, 4 } Inicialmente A tiene 2, B tiene 2. Luego P(0) = (0,0,1,0,0) Escribe la matriz de transición de orden 4. Calcula P4 y luego P(4)=P(0) .P4, comprueba que da (3/8, 0, 2/8, 0, 3/8 ). Acaba la partida y gana A, tiene 4 y B tiene 0. La solución pedida es el último número (A tiene 4 billetes): 3/8 la probabilidad de que A gane después de 4 jugadas. (Pulsar con el botón derecho del ratón una vez para que se puedan introducir todos los valores) |
|||||||||||||||
Para contestar al segundo apartado hay que utilizar la escena siguiente: Llamando A=I-M, calculamos F=A-1 Y sumar los números de la fila 2 de F (solución: 4 lanzamientos) 4º)ndicar la interpretación de cada elemento de F ( Ejemplo.1.5: número medio de veces que tiene 1 billete si partió con 1 billete, antes de terminar la partida) . 5º)Indicar la interpretación dede la suma de las filas de F. 6º)Interpretar los elementos de F.Q. Por ejemplo 0.75 (primer elemento de esa matriz F.Q) representa la probabilidad de que llegue al estado absorbente 0 (quedarse sin dinero) si empezó con 1 billete (estado no absorbente).
|
|||||||||||||||
|
|||||||||||||||