Pagina nueva 1

CADENAS DE MARKOV-II

(Es conveniente repasar el producto de matrices)

PROBABILIDAD DE TRANSICIÓN EN k PASOS.

Es la probabilidad de que un proceso pase del estado a_i al estado a_jen k pasos . se escribe

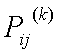
para i,j=1,2,3,....,n. Estas probabilidades se pueden ordenar en una matriz que se llama matriz de transición en k pasos:

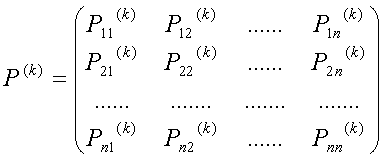
Para calcular esta matriz tenemos el método deducido del siguiente teorema que podéis comprobar para k=2 ó k=3 con los resultados de la escena y el ejercicio1 de la página anterior..

Teorema:

Si P es la matriz de transición de una cadena de Markov, entonces la matriz de transición de k pasos es la k-ésima potencia de P


	1º) En una ciudad existen dos partidos políticos, uno de derechas y otro de izquierdas. Los alcaldes son elegidos por un período de un año y se ha observado que la probabilidad de que a un alcalde de derechas suceda otro del mismo signo político es 3/5 y que a un alcalde de izquierdas siga otro de izquierdas es 1/2. a)Supongamos que en 2005 hay alcalde de izquierdas. ¿Cuál será la probabilidad de que en 2008 siga un alcalde de izquierdas al frente del concejo ? 2º) Un hombre conduce su coche o toma el tren para ir a trabajar cada día. Supongamos que nunca toma el tren dos días seguidos; pero si conduce para ir a trabajar, entonces al día siguiente es tan probable que conduzca de nuevo como que tome el tren. a) Escribe la matriz de transición del proceso. b) Calcula la probabilidad de que vaya en coche, cuatro días después de haber ido en tren.

	1º) Un ascensor de un edificio con bajo y dos pisos realiza viajes de uno a otro piso (lleno o vacío de ocupantes). El piso en el que termina el viaje n-ésimo del ascensor sigue una cadena de Markov. Se sabe que la mitad de los viajes que parten del bajo se dirigen a cada uno de los otros dos pisos , mientras que si un viaje comienza en el primer piso, sólo el 25 % de las veces finaliza en el segundo. Por último, si un trayecto comienza en el segundo piso, siempre termina en el bajo. A) Calcular la matriz de probabilidades de transición de la cadena. B) Dibujar su gráfico asociado. Es regular. C)¿Dónde es más probable que esté el ascensor después de cuatro viajes, si salió del Bajo? 2º) Una familia planifica cada año sus vacaciones de la siguiente manera. Si un año va a la montaña al año siguiente va al mar y al segundo año descansa en la casa. Pero al año siguiente es igualmente probable que se traslade al mar o a la montaña. En 2005 quedarán en casa. ¿Dónde es más probable que pasen sus vacaciones en el año 2010?

PROBABILIDADES TOTALES.

La probabilidad de que el proceso se encuentre en el estado a_i después de k pasos recibe el nombre de

probabilidad total o absoluta .

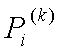A cada paso k le corresponde un vector estocástico formado por todas las probabilidades totales de ese paso:

en particular el vector de probabilidad inicial:

descrito en la primera escena de la página 1, que corresponde a la distribución de probabilidades de paso 0.

El siguiente teorema nos proporciona un método para calcular las probabilidades absolutas correspondientes a una prueba k del sistema:

Teorema: En una cadena de Markov con matriz de transición P se obtiene lo que sigue:

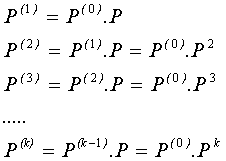
Es decir las distribuciones de probabilidad del paso k se pueden calcular multiplicando el vector de probabilidad inicial por la potencia correspondiente de la matriz de transición

1º) Dada la matriz de transición

con distribución de probabilidad P⁽⁰⁾=(1/3   2/3). Definir y hallar

2º) En una ciudad existen dos partidos políticos, uno de derechas y otro de izquierdas. Los alcaldes son elegidos por un período de un año y se ha observado que la probabilidad de que a un alcalde de derechas suceda otro del mismo signo político es 3/5 y que a un alcalde de izquierdas siga otro de izquierdas es 1/2. ¿Cuál serán las probabilidades de cada partido en el año 2010?

3º)Un hombre conduce su coche o toma el tren para ir a trabajar cada día. Supongamos que nunca toma el tren dos días seguidos; pero si conduce para ir a trabajar, entonces al día siguiente es tan probable que conduzca de nuevo como que tome el tren. si se sabe que el primer día de trabajo el hombre lanza un dado para decidir que si sale un 6 lleva el coche y si no va en tren. Calcula la distribución de probabilidad después de cuatro días.

4º)Un supermercado realiza la experiencia siguiente en relación con las preferencias de sus clientes. Se observa que: El 80% de las personas que compran un día el producto A repite al día siguiente. El 60% de los que no lo compran el producto A un día, lo compran al día siguiente. Si el 50% compró el producto un día determinado, ¿qué podemos predecir para la compra del producto el segundo día? ¿Y para el tercero?

1º) Una persona puede escoger entre tres restaurantes para comer diariamente. si un día escoge el restaurante A, al día siguiente escoge el B y al día siguiente del B siempre el C, pero cuando va a C es igualmente probable que al día siguiente vaya a A o a B. Escribir la matriz de transición del proceso y calculando después la tercera potencia de esa matriz, estimar a) la probabilidad de que vaya a B tres días después de ir a A. b) Las probabilidades absolutas de ir a cada restaurante después de cuatro días.



  María Blanca Gómez Rodríguez

Ministerio de Educación, Cultura y Deporte. Año 2005


	1º) Dada la matriz de transición con distribución de probabilidad P⁽⁰⁾=(1/3 2/3). Definir y hallar 2º) En una ciudad existen dos partidos políticos, uno de derechas y otro de izquierdas. Los alcaldes son elegidos por un período de un año y se ha observado que la probabilidad de que a un alcalde de derechas suceda otro del mismo signo político es 3/5 y que a un alcalde de izquierdas siga otro de izquierdas es 1/2. ¿Cuál serán las probabilidades de cada partido en el año 2010? 3º)Un hombre conduce su coche o toma el tren para ir a trabajar cada día. Supongamos que nunca toma el tren dos días seguidos; pero si conduce para ir a trabajar, entonces al día siguiente es tan probable que conduzca de nuevo como que tome el tren. si se sabe que el primer día de trabajo el hombre lanza un dado para decidir que si sale un 6 lleva el coche y si no va en tren. Calcula la distribución de probabilidad después de cuatro días.
4º)Un supermercado realiza la experiencia siguiente en relación con las preferencias de sus clientes. Se observa que: El 80% de las personas que compran un día el producto A repite al día siguiente. El 60% de los que no lo compran el producto A un día, lo compran al día siguiente. Si el 50% compró el producto un día determinado, ¿qué podemos predecir para la compra del producto el segundo día? ¿Y para el tercero?

	1º) Una persona puede escoger entre tres restaurantes para comer diariamente. si un día escoge el restaurante A, al día siguiente escoge el B y al día siguiente del B siempre el C, pero cuando va a C es igualmente probable que al día siguiente vaya a A o a B. Escribir la matriz de transición del proceso y calculando después la tercera potencia de esa matriz, estimar a) la probabilidad de que vaya a B tres días después de ir a A. b) Las probabilidades absolutas de ir a cada restaurante después de cuatro días.