

CADENAS DE MARKOV-I
| 1.CADENAS FINITAS DE MARKOV |
Muchos experimentos de Ciencias, Economía, Ingeniería, ...etc., consisten en sucesiones finitas de pruebas cada una de las cuales tiene un número finito de sucesos con probabilidades dadas. Procesos de este tipo reciben el nombre de Procesos estocásticos.
▪ Ejemplo 1. Escogemos 4 estudiantes al azar en una clase formada por 10 chicos y 5 chicas.
Con la ayuda de un diagrama en árbol y el teorema de la multiplicación podemos calcular las probabilidades de elegir chico o chica en cada uno de los cuatro pasos. La probabilidad de que ocurra un suceso en una prueba dependerá de qué ocurra en todas las anteriores.
Por ejemplo la probabilidad de que hayan sido elegidos chico, chica, chica, chica en ese orden sería:
(sucesos dependientes)
(expresamos con los subíndices el paso en qué sucede)
P(O1∩A2∩A3∩A4)=P(O1).P(A2/O1).P(A3/O1∩A2).P(A4/O1∩A2∩A3)=
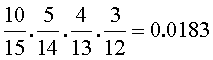
Ejemplo 2. Sea el experimento de tirar dardos 4 veces sobre una diana con probabilidad de acertar cada vez igual a 0.4.
Otra vez es una sucesión de 4 pruebas y cada una de ellas tiene dos acontecimientos posibles: acertar o errar. Pero ahora las pruebas son independientes y, por lo tanto, la probabilidad de que ocurra un suceso determinado en una de las pruebas es independiente del resultado de las anteriores.
Por ejemplo la probabilidad de que hayan ocurrido acierto, error, error, error en ese orden sería:
P(A1∩E2∩E3∩E4)=P(A1).P(E2).P(E3).P(E4)= (0.4).(0.6).(0.6).(0.6)= 0.0864
▪ Ejemplo 3. Durante las cuatro horas a la semana que tienen los alumnos de Estadística se reparten entre dos aulas: o van al aula de Informática, o trabajan en clase. Nunca van a los ordenadores dos días seguidos pero si un día trabaja en clase es igualmente probable que el día siguiente realice cualquiera de las dos tareas. El lunes , el profesor tira una moneda para decidir a dónde van.
Una vez más el experimento consta de cuatro pruebas con dos sucesos en cada una de ellas (ir al aula de informática o no ir). A diferencia de los experimentos anteriores, la probabilidad de que en cada una de las pruebas ocurra un acontecimiento depende únicamente del resultado de la prueba anterior. Procesos de este tipo (ejemplo 3) son el objeto de estudio en este tema.
Probabilidad de ir al aula de informática sólo el primer día: (I :"ir al aula de informática"; C=" trabaja en clase")
P( I1∩C2∩C3∩C4)= P(I1).P(C2/I1).P(C3/C2).P(C4/C3)=
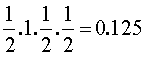
Ejercicio 1
Puedes escribir los valores de las probabilidades de la matriz de transición en el marco superior de la escena directamente y pulsando enter (en forma decimal 0.75 o en forma de fracción, 3/4, por ejemplo) o pulsando los cursores hasta encontrarla
| Si llamamos
a los posibles estados de este experimento : a1="ir al aula de Informática" a2= "trabaja en clase" p1(0)=probabilidad inicial de ir al estado a1=1/2 p2(0)=probabilidad inicial de ir al estado a2=1/2
|
p11=probabilidad
de ir del estado a1
al estado
a1=0 p12=probabilidad de ir del estado a1 al estado a2=1 p21=probabilidad de ir del estado a2 al estado a1=1/2 p22=probabilidad de ir del estado a2 al estado a2=1/2 Se llaman probabilidades de transición entre estados de la cadena
|
|
A
lo largo de cuatro días seguidos (n=3 pasos) ¿Qué ocurrirá? 1º). Observa los caminos que hay para ir de a1(primer día) a a1 el cuarto día (en n=3 pasos). La escena te da la probabilidad que será llamada p11(3). Comprueba que te da lo mismo en el cuaderno y con la calculadora, haciendo como en el ejemplo anterior. Es decir, es la probabilidad de ir al aula de informática en tres pasos (el cuarto día) sabiendo que también fueron el primer día. 2º) Lo mismo para ir de a1 a a2 en tres pasos. p12(3).Traduce este resultado a texto, como la penúltima línea. 3º) ¿Y de a2 a a1 en tres pasos? p21(3). Traduce este resultado a texto 4º) Lo mismo de a2 a a2 en tres pasos. p22(3)..5º)Observa que tiene que ocurrir que p1(0)+ p2(0)=16º)Observa que tiene que ocurrir que p11+ p12=1 p21+ p22=1 7º)Calcula la probabilidad de ir al aula de informática en tres pasos (el cuarto día): p1(3). ¿Qué diferencia observas entre la cuestión 1ª y esta?¿Qué probabilidades intervienen? |
Ejercicio 2
Calcular las siguiente probabilidades usando el diagrama en árbol:
a) Probabilidad de ir al aula de informática en el tercer día si se sabe que el lunes han quedado en clase. p21(2).
b) Probabilidad de ir al aula de informática en el tercer día si se sabe que el lunes han quedado han ido.
p11(2).c) Probabilidad de no ir al aula de informática en el tercer día si se sabe que el lunes han ido.
p12(2).d) Probabilidad de no ir al aula de informática en el tercer día si se sabe que el lunes tampoco han ido han ido.
p22(2)e) Calcular la probabilidad de ir al aula de informática el tercer día.
p1(2).(Aquí hay que tener en cuenta las probabilidades iniciales
p1(0) y p2(0)) (SOLUCIÓN: p1(2)=p11(2).p1(0)+ p21(2).p2(0)=0.375 )f) Calcular la probabilidad de no ir al aula de informática el tercer día.
p2(2)g) Probabilidad de ir al aula de Informática en el cuarto día.
p1(3).h) Calcular la probabilidad de no ir al aula de informática el tercer día.
p2(3)Copia los resultados de estas cuestiones en tu cuaderno y las aclaraciones que consideres oportunas.
Estos resultados se pueden generalizar a n pasos (en vez de cuatro días seguidos, tres pasos) para cualquier proceso del tipo anterior y cualquier número de estados (sólo eran dos en el caso anterior). Pero observar la dificultad de realizar los cálculos con el método anterior para un número de pasos mayor y un número mayor de estados. Esto lo estudió Markov con el método que de forma simplificada (propia de este nivel) exponemos a continuación.
Cadenas finitas de Markov.
| Un proceso estocástico finito en el que se verifica que el resultado de una prueba determinada depende como máximo de la prueba inmediatamente anterior y no de ninguno de los resultado previos , recibe el nombre de Cadena finita de Markov. |
En una cadena de Markov hay:
Un espacio de estados E={a1,a2,a3,.... an } (Cada estado son todos los resultados posibles de cada una de las pruebas).
Cuando el resultado de la prueba r es ai decimos que el proceso está en el estado ai en el paso r-ésimo.
Para cada dos estados ai y aj , la probabilidad de que el estado aj ocurra inmediatamente después que el estado ai, que llamaremos probabilidad de transición del estado
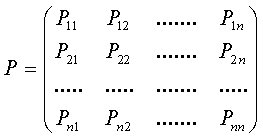
El
vector formado por las probabilidades del estado inicial del sistema., llamado
vector de probabilidad inicial
Obsérvese que la suma de las probabilidades que expresan
los elementos del vector debe ser igual a 1 y, por lo tanto, el vector de
probabilidad inicial es un vector estocástico.
2º)
Un alumno acude al Instituto, o bien en bicicleta o andando. Si un día
emplea la bicicleta, al día siguiente utilizará la bicicleta con
probabilidad 1/2, y si va andando al día siguiente también lo hará con
probabilidad 3/4. Calcula el espacio de
estados, la matriz de transición del proceso .También el diagrama del
proceso. Copia los resultados en tu cuaderno.
3º)En una región, si un día hay
niebla al siguiente llueve pero, si llueve , el día siguiente es soleado. Se
tiene observado que las probabilidades de que a un día con sol suceda un día
nublado o lluvioso son, respectivamente, 0.4 y 0.6. Definir el espacio de
estados y la matriz de transición del proceso. Copia los resultados en tu
cuaderno. 4º)
Una Central de seguridad vial chequea a menudo uno de tres puntos
conflictivos A, B y C. La probabilidad de que un día controle el mismo lugar
que el día anterior es 1/2 y las probabilidades de que controle uno
cualquiera de los otros dos puntos restantes son iguales. Definir el espacio
de estados y la matriz
de transición del proceso. Copia los resultados en tu cuaderno.
Utilizar estas escenas
para resolver ejercicios del boletín de clase en los que se pida la matriz de
transición del proceso y el diagrama de transición.
En esta matriz cada línea contiene las probabilidades de
transición de un estado determinado a todos los demás, es decir, las
probabilidades de todos los resultados posibles de la próxima prueba. La suma de
todas estas probabilidades debe de ser 1 y, por tanto,
la suma de los elementos de cada fila de la
matriz de transición vale 1. Como además todos los elementos de
la matriz son
≥0
por ser probabilidades, la matriz de transición es una matriz estocástica.
![]()
1º)Escribe el espacio de estados
y la matriz de transición para el ejemplo de la escena anterior. Cópialos en
tu cuaderno.