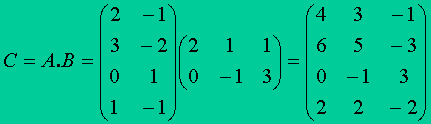
PRODUCTO DE MATRICES
Para poder multiplicar dos matrices A de orden mxp y B de orden pxq ha de ocurrir:
que el número de columnas de A sea igual al número de filas de B : p
además observa que el resultado es otra matriz
C = A.B
que tiene orden mxq,es decir el número de filas de A y el número de columnas de B.
Ejemplo:
|
fila1xcolumna1 2*2+(-1)*0 |
fila1xcolumna2 2*1+(-1)*(-1) |
fila1xcolumna3 2*1+(-1)*3 |
|||||||||||||||||
| 2 | -1 | 4 | 3 | -1 | c11 | c12 | c13 | ||||||||||||
| C=A.B= | 3 | -2 | . | 2 | 1 | 1 | = | 6 fila2*col 1 | 5 fila2*col2 | -3 fila2*col3 | c21 | c22 | c23 | ||||||
| 0 | 1 | 0 | -1 | 3 | 0 fila3*col1 | -1 fila3*col2 | 3 fila3*col3 | c31 | c32 | c33 | |||||||||
| 1 | -1 | 2 fila4*col1 | 2 fila4*col2 | -2 fila4*col3 | c41 | c42 | c43 | ||||||||||||
|
4 x2 |
2x 3 | 4 x 3 | |||||||||||||||||
Cada elemento cij (i indica la fila que ocupa y j la columna ) de la matriz C se obtiene multiplicando escalarmente la fila i de A por la columna j de B.
Escrito correctamente:
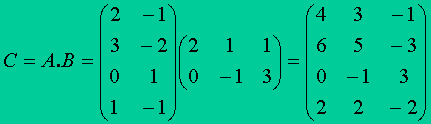
Comprueba con estos ejemplos que :
el producto de matrices no es conmutativo:
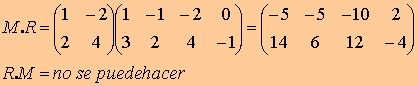
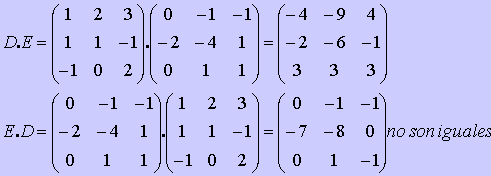
Pn
Ten en cuenta que:
P2=P.P y que P3=P.P2
y así sucesivamente.
Calcula la
potencia cuarta de:
![]()
Calcula la potencia cuarta de la matriz, con la escena y sin ella.
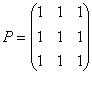
| María Blanca Gómez Rodríguez | |
 |
|
| Ministerio de Educación. Año 2005 | |