
 |
TEORÍA |
| Bloque: Análisis | |
| REPASA |
LEE DETENIDAMENTE
Función compuesta:
Dadas dos funciones f y g, llamamos función compuesta de f y g, escribimos gof y leemos “f compuesta con g”, a la función gof(x)=g[f(x)].
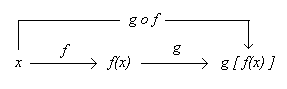
Llamamos función compuesta de g y f, escribimos fog y leemos “g compuesta con f”, a la función fog(x)=f[g(x)].
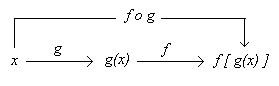
La composición de dos funciones no es conmutativa, es decir en general fog es distinto de gof.
Función exponencial
Llamamos función exponencial a la que tiene por expresión analítica y=ax, siendo a un número real positivo distinto de 1.
Son funciones continuas cuyo dominio es el conjunto de los números reales.
Son funciones positivas que pasan por los puntos (0,1) y (1,a).
Si a>1, son funciones crecientes en todo su dominio.
Para valores de x muy grandes pero negativos, f(x) toma valores próximos a cero.
Para valores de x muy grandes, f(x) toma valores también muy grandes.
Cuanto mayor sea el valor de a, más rápido crecen estas funciones.
Si 0<a<1, son funciones decrecientes en todo su dominio.
Para valores de x muy grandes pero negativos, f(x) toma valores muy grandes.
Para valores de x muy grandes, f(x) toma valores próximos a cero.
Cuanto menor sea el valor de a, más rápido decrecen estas funciones.
|
|
|
|
| José María Vázquez de la Torre Prieto | ||
 |
||
| Ministerio de Educación, Cultura y Deporte y Ciencia. Año 2006 | ||