
 |
INTEGRAL DEFINIDA |
| Análisis | |
| 1. DEFINICIÓN DE LA INTEGRAL UNA FUNCIÓN |
Si hacemos tender n (número de puntos de la partición) hacia infinito, o lo que es lo mismo las bases de los rectángulos hacia cero, podremos calcular el límite tanto de las sumas superiores de Riemann como de las sumas inferiores. Si existen ambos límites y son iguales diremos que la función f es integrable y definiremos la integral definida entre a y b de f como el resultado de este límite, es decir A los extremos del intervalo a y b se les llama límite inferior y superior de integración, respectivamente. |
| 2. SIGNO DE LA INTEGRAL DEFINIDA | |||
| Según la definición de integral definida, hay una relación intrínseca entre este concepto y el área del trapecio mixtilíneo. Pero, ¿es lo mismo? | |||
1.- Observa la siguiente escena. Todas las funciones que aparecen son constantes aunque no necesariamente positivas. Compara el valor del área del recinto con la integral definida en ese intervalo. ¿Podemos decir que ambos conceptos son iguales?.
2.- Analiza la definición de integral definida e intenta dar una explicación a estos hechos. 3.- Determina la relación entre el área del recinto mixtilíneo y la integral definida para funciones negativas. 4.- ¿Podría darse el caso de un recinto mixtilíneo cuya superficie sea no nula y su integral definida valga 0?. Pon ejemplos. |
|||
| 5.- Establece la relación entre el signo de la función y el signo de la integral definida de esa función. | |||
| 3. PROPIEDADES ELEMENTALES DE LA INTEGRAL DEFINIDA | |||
Si c en un
punto interior al intervalo [a,b], entonces 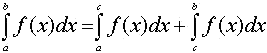 |
|||
|
6.- Observa la relación entre las áreas rosa y naranja. Relaciona la integral de una función entre a y b , con las integrales de la misma función entre [a,c] y [c,b]. 7.- ¿Se puede generalizar el resultado para funciones que nos sean necesariamente positivas?
|
|||
| La integral definida de una función f cuando a=b es igual a cero. | |
8.- Modifica el valor de b y observa las consecuencias. 9.-Demuestra analíticamente el resultado. 10.-¿Se podrá afirmar que si b1<b2 entonces la integral entre a y b1 es menor que la integral entre a y b2?. ¿En qué condiciones esta afirmación es cierta?. 11.-Y en el caso de dos funciones distintas f1 y f2 , de manera que f1<f2, entonces ¿La integral entre a y b de f1 es menor que la integral entre a y b de f2?. 7.- ¿Se puede generalizar el resultado para funciones que nos sean necesariamente positivas?. 12.-Utilizando las propiedades 1 y 2, demuestra analíticamente el resultado |
|
| 13.- ¿Podríamos haber deducido esta igualdad observando los resultados de la actividad 2?. | |
La integral definida es lineal.
|
|||||
14.- En la escena contigua están representadas dos funcione f y g y la suma de ambas h. Comprueba que la relación h(x)=f(x)+g(x) es cierta para cada x
15.- Observa la relación que hay entre los rectángulos que forman las sumas de Riemann para f, g y h.
|
|||||
| 16.-Enuncia la relación que
hay entre las integrales de f, g y su suma f+g. ¿Es el resultado extensible a la
diferencia?. Indicación: Utiliza las propiedades de los límites. 17.-¿Qué relación habrá entre la integral de una función y la del doble de la misma función?. 18.-Enuncia una propiedad que relacione la integral de una función por un número real y la integral de esa función. |
|||||
| 4. TEOREMA DE LA MEDIA | |
Dada una función
continua f definida en [a,b], existe un valor c de manera que 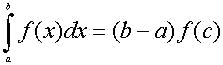 |
|
19.- Observa la elección de los rectángulos en cada partición y el resultado de las áreas gris y naranja. ¿Qué es lo que ocurre?. ¿Por qué?. 20.-Calcula las áreas de los rectángulos que aproximan a la integral. ¿Por qué existe un valor de x en cada base de los rectángulos, de manera que la imagen de la función en ese punto es una altura tal que multiplicada por la base da exactamente el área del recinto naranja al que pretendemos aproximar?. ¿A qué teorema conocido se puede estar haciendo referencia?. 21.-Cuando n=1 obtén las fórmulas de los rectángulos que por exceso y defecto aproximan al recinto naranja. |
|
22.-Haz una
comparación entre las fórmulas obtenidas en el ejercicio anterior y el recinto naranja.
Obtén la siguiente desigualdad 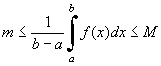 con
m y M el mínimo y máximo de f en [a,b] respectivamente. con
m y M el mínimo y máximo de f en [a,b] respectivamente.23.-Utiliza el teorema del valor medio para la función f y demuestra el teorema de la media. |
|
| 5. EL VALOR ABSOLUTO DE LA INTEGRAL Y LA INTEGRAL DEL VALOR ABSOLUTO | ||
24.- Observa las representaciones gráficas de una función f y del valor absoluto de esa función |f|. El área encerrada entre la curva y el eje de abscisas en ambos casos es la misma, sin embargo ¿La integral definida de f y |f| son iguales? 25.- Determina en qué situaciones ambas integrales son la misma. 26.- ¿Qué relación de orden existirá entre el valor absoluto de la integral de una función y la integral del valor absoluto de esa función?.
|
||
Dada una función f se
verifica que 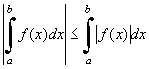 |
||
| Enrique Martínez Arcos | |
 |
|
| Ministerio de Educación, Cultura y Deporte. Año 2001 | |

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.