El concepto se derivada se aplica en los casos donde es necesario medir la rapidez con que se produce el cambio de una situación. Por ello es una herramienta de cálculo fundamental en los estudios de Física, Química y Biología. También en las ciencias sociales como la Economía y la Sociología  se utiliza el análisis matemático para explicar la rapidez de cambio en las  magnitudes que les son propias.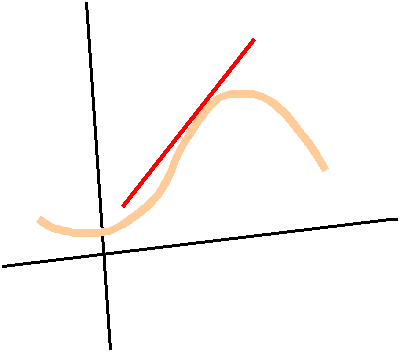

Conocer la variación de una función en un intervalo grande no informa suficientemente bien en el sentido de entender como se produce dicha variación. Se necesita estudiar variaciones de la función en intervalos cada vez más pequeños para llegar a entender el concepto de variación instantánea o referida a un punto, es decir el de derivada en un punto.

Un hallazgo importante en el estudio de la derivada  de una función es que la pendiente o inclinación de la recta tangente a la curva en un punto representa la rapidez de cambio instantáneo. Así pues cuanto mayor es la inclinación de la recta tangente en un punto mayor es la rapidez de cambio del valor de la función en las proximidades del punto.

El concepto de derivada segunda  de una función - derivada de la derivada de una función- también se aplica para saber si la rapidez de cambio se mantiene, aumenta o disminuye. Así el concepto de convexidad y concavidad -aspectos geométricos o de forma- de una función están relacionados con el valor de la derivada segunda.

La derivabilidad de una función en un punto (propiedad relativa a la existencia de tangente en un punto) está asociado al de continuidad. Este aspecto también será tratado en esta unidad.

Finalmente veremos la relación que tiene la derivada  con los problemas de optimización de funciones. Estos problemas decimos que son de máximo o de mínimo (máximo rendimiento, mínimo coste, máximo benefício, mínima aceleración, mínima distancia, etc).

• Adquirir con claridad el concepto de derivada de una función en un punto.

• Distinguir entre derivada en un punto x=x₀ de una función f(x) y función derivada de f(x).

• Calcular rectas tangentes a una curva f(x).

• Aprender la técnica de derivación de funciones f(x).

• Interpretar aspectos de crecimiento/decrecimiento, concavidad/convexidad de funciones a partir de la función derivada y derivada segunda de una función f(x).

• Determinación de valores máximos y mínimos de funciones f(x) y resolver problemas de optimización