|


|
TASA DE
VARIACIÓN INSTANTÁNEA
|
|
|
Concepto
Continuamos
con el ejemplo anterior. Una bola es lanzada desde el suelo
verticalmente y hacia arriba. La función altura-tiempo es y=f(t)=50t
- 5t2
Recordemos que podíamos
calcular la altura en cualquier instante pero no podíamos tener
información precisa de como está variando la altura en un instante
determinado, por ejemplo, en t0=2 segundos. Este dato se
denomina variación instantánea.
Para obtener esta
información vamos a estudiar cómo varía la altura en intervalos que
empiezan en t0=2 y tiene amplitudes h cada vez más
pequeños. Es decir calculemos las tasas de variación media en los
intervalos sucesivos [t0,t0+h] tal que h tienda a
0.
Consideremos el intervalo
[2,5] con una anchura h=3 segundos
|
|
Para conocer la variación
instantánea en t0=2 segundos tenemos que calcular la
variación media (TVM) correspondiente a un intervalo [2,2+h], tendiendo
h a cero.
Has podido observar en la
gráfica que las distintas tasas de variación media son las pendientes
de la recta secante a la curva por los puntos P(2,f(2)),
Q(2+h,f(2+h))
y que cuando h tiende a cero el punto Q
se desplaza sobre
la gráfica hasta confundirse con el punto P
a la vez que las sucesivas rectas
secantes por P y Q
tienden hacia la recta tangente a la gráfica en el punto P.
Geométricamente, la TVM es la
pendiente de la secante por P y Q
y por tanto la variación instantánea en P será como caso límite la
pendiente de la recta tangente en P.
La variación instantánea en t=2 se
representa por f ' (2) y se conoce como la derivada de la función f(t)
en t=2
La expresión analítica de la
derivada en el punto t=2
Viene dada por el valor del siguiente
límite:
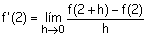
|
Pasemos al
intervalo [2,4] con una anchura h=2
Siguiendo esta sucesión
podemos considerar una anchura arbitrariamente pequeña, p.e. h=0.05
segundos ¡ 5 centésimas de segundo !. Con lo que la tasa TVM en este
intervalo medirá casi la variación instantánea en t0=2
segundos.
La sucesión de las TVM
tiene como límite la variación instantánea en t0=2
segundos cuyo valor es
f '
(2)=30 m/s |
|
|
Derivada
de una función en un punto
Dada una función y=f(x)
y un punto de abcisa x=a, se define la derivada de f(x) en x=a y se
designa f '(a), como el límite siguiente, si es que existe,
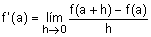
Si expresamos el valor
variable a+h = x, tenemos que h= x-a de tal manera que cuando h®0
se cumplirá que x®a.
La derivada en x=a
también puede ser expresada de la siguiente manera
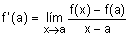
y representa
desde le punto de vista geométrico la pendiente de la recta tangente a
la gráfica de la función y = f(x) en el punto de abcisa x=a
|
|
Ecuación de la recta tangente
Si una recta tiene un ángulo de
inclinación a
decimos que su pendiente es m = tg(a).
La forma explicita de la ecuación de una
recta es y = mx + n. Si (x0,y0) es un punto de
dicha recta se cumplirá y0=mx0+n y restando estas
dos expresiones se obtiene y-y0=m(x-x0) es decir
y=m(x-x0)+y0
Sea y=f(x) una cierta función que admita
una recta tangente en el punto P(a, f(a)). Este punto también
pertenecerá a la recta tangente a la curva y=f(x) y la
pendiente de la recta es m = f '(a).
Es decir tenemos un punto de la recta x0=a,
y0=f(a) y conocemos su pendiente, luego la ecuación de la
recta tangente a y=f(x) en x=a es
y=f '(a)(x-a)+f(a)
|
EXPERIMENTA
1.- En el ejemplo de la
figura anterior, calcula las siguientes derivadas: f ' (-2), f ' (-1), f
' (0), f '(2.5). Anota los resultados en tu cuaderno
2.- Comprueba que en los
puntos donde la función crece la derivada es positiva, en los puntos
donde la función decrece la derivada es negativa.
3.- ¿Dónde el crecimiento es mas rápido
en x= -2 ó en x = -1.5?¿Dónde es más lento el decrecimiento en
x=0.5 ó en x=1.5?
4.- ¿Qué debe de ocurrir
en los puntos donde hay un máximo o un mínimo local?
5.- Observa la recta
tangente en distintos puntos y comprueba que la ecuación de la recta es
la que hemos deducido anteriormente.
|
|
Relación entre el
crecimiento de una función en un punto y el valor de su derivada
Recuerda que en la unidad
didáctica que hace referencia al estudio del crecimiento de una
función se decía
Función creciente en
x=a. 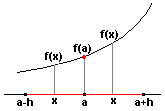
Se dice que y = f(x) es
creciente en un punto x=a de su dominio si existe un entorno de dicho
punto, (a-h,a+h) tal que si x pertenece a este entorno y x£a
entonces f(x)£f(a) y si x³a
entonces f(x)³f(a).
Por tanto resulta que en
ambas situaciones el signo de (x-a) es igual al signo de f(x)-f(a), para
cualquier x perteneciente al entorno de a; consecuentemente la tasa de
variación media TVA[a,x] es positiva y su límite cuando x®
a también, es decir f ' (a) >0. Recíprocamente también es cierto
que si f ' (a) >0 entonces TVM[a,x] >0 y la función es creciente
en x=a.
f
(x) es creciente en x=a equivale a f ' (a) > 0
Función
decreciente en x=a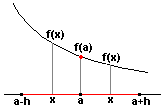
Se dice que
y = f(x) es decreciente en un punto x=a de su dominio si existe un
entorno de dicho punto, (a-h,a+h) tal que si x está en este entorno y x£a
entonces f(x)³f(a) y si x³a
entonces f(x)£f(a).
En ambas
situaciones se cumple que el signo de (x-a) es distinto que el signo de
f(x)-f(a), para cualquier x perteneciente al entorno de a;
consecuentemente la tasa de variación media TVA[a,x] es negativa y su
límite cuando x® a también, es decir f '
(a)<0. La proposición recíproca es también cierta, si f ' (a) >
0 entonces la función es decreciente en x=a.
f(x)
es decreciente en x=a equivale a f ' (a) < 0
|
|
Cálculo de derivadas
Sea la función y=f(x) = x2
-2x -1. Queremos calcular la derivada en el punto de abcisa x=2.
La ordenada correspondiente
es f(2) = -1
Veamos el procedimiento a
seguir:
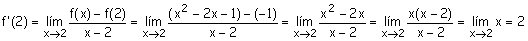
Sigamos con otro ejemplo y
calculemos para la función anterior la derivada en x = 0.5
La ordenada para x = 0.5 es
f(0.5)= -1.75
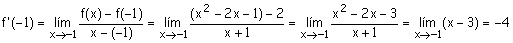
Comprueba en la siguiente
escena estos resultados:
|
|
|
EXPERIMENTA
1.- En la escena actual,
observa el valor de f(3).
2.- Observa el valor de la
derivada f '(3). Realiza el procedimiento aprendido para calcular f '(3)
y comprueba el resultado.
3.- Calcula la ecuación
recta tangente a la curva en x=3 y comprueba el resultado con el de la
escena correspondiente.
4.- Calcula el intervalo de
crecimiento y el intervalo de decrecimiento de la función.
5.- ¿Determina el punto
donde f ' (a) = 0? ¿Cómo se llama este punto?
6.- Hallar el
valor de a perteneciente al intervalo [-1,1] para el que se
cumple que la tasa de variación media TVM[-1,1] coincide con la
tasa de variación instantánea f ´(a)
|
| Derivabilidad
y continuidad
Estudiaste el concepto de función
continua en un punto. Hagamos memoria:
Una función y=f(x) es continua en x=a si y solo si f(a+h)-f(a) ®
0 cuando h ®
0. En otros términos, a
variaciones muy pequeñas de la x en torno de a le
corresponde variaciones muy pequeñas de f(x) en torno de f(a).
Designando x=a+h, tenemos que h=x-a y se
cumple que el "límite de la función es el valor de la función en
el límite"
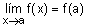
Esta definición obliga a
las siguientes cosas:
a) Que la función este
definida en x=a, ya que ha de existir f(a)
b) Que exista el límite de
f(x) cuando x®a. Es decir el límite por la
derecha y por la izquierda de a han de coincidir:
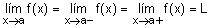
c) f(a) = L
Si alguna de estas cosas no
se cumple la función es discontinua en a.
La derivabilidad de f(x) en
x=a es una condición analítica más fuerte que la continuidad, puesto
que
Si una función
es derivable en x = a, entonces la función es continua en x=a
Una función puede ser
continua en un punto y no tiene por qué ser derivable.
Demostremos esto:
Supongamos y=f(x) derivable
en x=a y veamos que pasa con la continuidad en x=a:
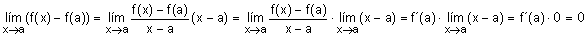
por lo que y=f(x) es continua
en x=a, pues
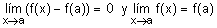
El siguiente ejemplo pone de
manifiesto lo que hemos dicho arriba.
|
|
|
La función
del ejemplo y=f(x) presenta las siguientes características
observables:
Tiene una
discontinuidad por salto finito en x= -1 y puesto que no
tiene tangente en x= -1 no es derivable en x = -1.
Tiene un punto
anguloso en x =2 y aunque es continua en él, la tangente por
la derecha tiene distinta pendiente que la tangente por la izquierda;
luego no es derivable en x=2
f ´(2-) =
-1.26 <> f ´(2+) = 1.26
Resumiendo:
| Si
f(x) Continua en x=a |
f(x)
puede ser derivable en x=a |
| f(x)
puede no ser derivable en x=a |
| Si
f(x) Derivable en x=a |
f(x)
es continua en x=a |
|
|
Ejercicios para probar la
continuidad y derivabilidad
El siguiente programa permite
definir funciones y=f(x) en dos trozos (-inf,x0) y [x0,+inf)
en el primero la función viene dada por la expresión f1(x)=ax2+bx+c
y en el segundo f2(x)=a´x2+b´x+c´, donde los coeficientes a, b, c,
a´, b´ y c´ pueden ser elegidos a voluntad. El problema consiste en ajustar
dichos coeficientes para que la función sea continua o derivable en x0,
según los ejemplos que se quieran estudiar.
Es decir la función se define
así:
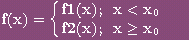
|
|
|
|
1:
Inicialmente
el programa considera la función
f(x) definida como f1(x)=x2+x+1, para x<0 y f2(x)=0.5x2+2,
para x>=0.
Como se puede apreciar la
función f(x) es discontinua por salto en x=0. Se le propone al estudiante que
modifique los parámetros de f2(x) para que la función sea continua, pero no
derivable en x=0. En este caso se deberá cumplir que el límite por la
izquierda en x=0 coincide con el límite por la derecha en x=0, es decir
f1(0-)=f2(0+)=1, pero la derivada por la izquierda f1´(0-) <> f2´(0+).
Ahora se trata de hacer derivable
la función cuando se cumpla que f1´(0-)=f2´(0+). Modificar los coeficientes
para conseguirlo. Observar que puede haber varias soluciones.
Anotar en el cuaderno la
definición de f(x) para que sea derivable en x=0 en 4 casos al menos.
2: Sea
la función
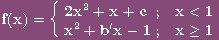
Ajustar los
coeficientes c y b´ para que la función sea continua y
derivable en x=1
En este caso la
solución es única.
El programa
Descartes permite hallar c y b´ mediante ensayo y error y requiere
tener un poco de paciencia hasta que el estudiante adquiera destreza sobre todo
averiguando como varía la forma de función al modificar los coeficientes.
El método
algebraico-analítico va directo a la solución. Intente el alumno
encontrar la solución antes de ver el siguiente cálculo.
Solución:
Para que la función
sea continua en x=1 se debe satisfacer f1(1-)=f2(1+), sustituyendo en f1(x) y
f2(x) para x=1 e igualando se obtiene la ecuación 3 + c = b´.
Para que la función
sea derivable en x=1 se debe satisfacer f1´(1-)=f2´(1+), es decir hay que
calcular las derivadas f1´(1-) y f2´(1+) e igualar.
f1´(x)=4x +1,
f2´(x)=2x+b´, por tanto 4 + 1 = 2 + b´, de donde b´ = 3 y
sustituyendo en la anterior ecuación entre c y b´ obtenemos
3 + c = 3 y por tanto c = 0.
3: Determinar
los parámetros c y b´ para que la función sea continua y
derivable en x=2
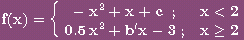
El alumno deberá
resolver este ejercicio utilizando el método de ensayo-error que proporciona el
programa y luego calculará los coeficientes con el método algebraico-analítico, como se hizo en el ejercicio anterior comprobando las
soluciones.
4: Hallar
los coeficientes b y c´ para que la función f(x) sea derivable
en x=- 2. Primero resuélvase mediante el programa Descartes y a continuación mediante el método
algebraico-analítico.
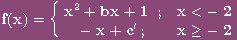
|
