LA FUNCIÓN DERIVADA

Hasta aquí nos hemos referido a la derivada de una función y=f(x) en un punto x = a de su dominio; el resultado es un número real, por tratarse de un valor límite

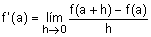
Consideremos la función y = 50t-5t² que representaba la posición vertical de una bola lanzada desde el suelo hacia arriba en función del tiempo. El dominio de definición es el intervalo [0,10] ya que no tiene sentido hablar de posiciones por debajo del nivel del suelo; el instante inicial es t=0 segundos (cuando es lanzada) y el final es t=10 segundos (cuando llega al suelo de caída).

Podemos observar que en cada instante t la bola tiene asociada una variación instantánea (su velocidad) que es la derivada f ' (t).

Existe una aplicación entre la variable t perteneciente a [0,10] y f'(t). Esta aplicación es una nueva función que convenimos en escribir y' = f '(t) y llamamos función derivada de y = f(t).

El siguiente es un cuadro de algunos valores de esta función:

 DOMINIO DE DERIVABILIDAD

También sabemos que es posible que la derivada de una función en un punto, no exista, en cuyo caso decimos que la función no es derivable en ese punto.

Decimos que una función es derivable en un intervalo abierto (x₁,x₂) de su dominio si lo es en cada uno de sus puntos. En general el conjunto de puntos donde la función es derivable constituye su dominio de derivabilidad.

Hay que observar que el dominio de derivabilidad de una función puede no coincidir con el dominio de la función. O dicho de otra forma, el dominio de la función f(x) puede no coincidir con el dominio de la función derivada f ´(x).

Ejemplo: Consideremos la función valor absoluto de x que queda definida de la siguiente manera:

El dominio de y=f(x) es R (conjunto de números reales) mientras que el dominio de y´ es R - {0} puesto que en x=0 la función f(x) presenta un punto anguloso y la pendiente por la izquierda  no coincide con la pendiente por la derecha.

La gráfica de la función derivada es:

Pues la pendiente de f(x) es constante y vale tg(45º)=+1 para x>0 y es constante y vale tg(135º)=-1 para x<0. En x = 0 no está definida la función derivada.

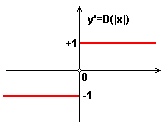Derivabilidad de las funciones polinómicas

En las escenas anteriores las funciones f(x) eran polinómicas y habrás observado:

1. Que el dominio de derivabilidad es el mismo que el de la función.

2. La función derivada es también polinómica y un grado menor.

Si f(x) e una función polinómica de grado n resulta que la derivada f ' (x) es de grado n-1

OTRAS FORMAS DE DESIGNAR LA DERIVADA

La función derivada de f(x) normalmente se designa por f´(x) como hemos hecho hasta ahora. Otras formas usadas son df(x)/dx o D_x[f(x)] que se lee como "derivada de la función f(x) respecto de x".

EXPERIMENTA:

1.- Observa la altura y la velocidad de la bola (derivada) en los siguientes instantes: t=1,5 ; t=5; t=10

2.- Determina dos instantes de tiempo para los que la altura de la bola es la misma f(t)=80. ¿Cuál es la derivada en cada uno de estos instantes? ¿Qué significa este resultado?

3.- Observa que cuando la función es creciente (la bola sube), la derivada es positiva y cuando la función es decreciente (la bola baja) la derivada es negativa.

4.- Observa que en la altura máxima la función pasa de ser creciente a ser decreciente y la derivada se hace cero. 

5.- Cuales son los dominios de definición de f(t) y f '(t)

En la siguiente escena se representa la función y=2x³-9x²+12x-3 y su derivada y' =6x²-18x+12

Trata de entender el significado:

El dominio de la función y=f(x) es R y puesto que es continua y no presenta puntos angulosos el dominio de derivabilidad es también R 

Los intervalos de crecimiento son (-infinito,1) y (2,+infinito).

Hay un intervalo donde la función decrece (-1,2).

Observa la función derivada f '(x): en los intervalos de crecimiento de f(x) la derivada es positiva (representación por encima del eje de abcisas OX) pues la recta tangente  tiene una inclinación entre 0º y 90º; en el intervalo de decrecimiento de f(x) la derivada es negativa (representación por debajo del eje OX) pues la recta tangente tiene un ángulo de inclinación entre 90º y 180º. Donde la función derivada corta al eje OX se cumple que f '(x)=0 pues la tangente a la curva y=f(x) es horizontal (ángulo de inclinación de 0º).

 1.- Localiza las coordenadas de los puntos máximo y mínimo locales.

2.- Observa que el crecimiento o decrecimiento de la curva f(x) es menor cuanto más próximos estamos de los puntos máximo y mínimo locales.

 3.- Observa que el crecimiento se hace muy rápido cuanto más nos alejamos a la derecha del mínimo y que el decrecimiento se hace muy rápido cuando nos alejamos a la izquierda del máximo.

Para calcular la derivada de y=f(x) en x=a, obteníamos el límite

puesto que ahora nos interesa obtener la expresión de la derivada para un punto cualquiera x, habrá que calcular

1.- Función incrementada:

f(x+h)

2.- Incremento de la función (variación):

f(x+h)-f(x)

3.- Cociente incremental (TVM):

4.- Límite del cociente incremental:

Calculemos mediante la Regla de los cuatro pasos, la función derivada:

1.- Función incrementada:

f(x+h) = 50(x+h)-5(x+h)² = 50(x+h)-5(x²+2xh+h²) = 50x+50h-5x²-10xh-5h²

2.- Incremento de la función:

f(x+h-f(x) = (50x+50h-5x²-10xh-5h²)-( 50x-5x²) = 50h-10xh-5h²

3.- Cociente incremental (TVM):

4.- Límite del cociente incremental:

f ' (x) = 50 - 10x

Comprobar este resultado con el que se daba en el estudio de la velocidad de la bola.

Es importante recordar este resultado pues ayudará a calcular funciones derivadas de polinomios sin tener que recurrir a la regla de los cuatro pasos.

Para ello es necesario conocer la propiedad de linealidad de las funciones derivadas que masamos a explicar seguidamente.

Sea y =f(x) e y = g(x) dos funciones que tienen el mismo dominio de derivabilidad. Se cumplirá que:

• La derivada de la suma f(x)+g(x) es igual a la suma de las derivadas f ' (x) + g ' (x):

[f(x)+g(x)]´= f ´ (x) + g´(x)

• Derivada de una constante k por una función f(x) es igual a la constante por la derivada de la función:

[k·f(x)]´= k·f ´(x)

Estas dos propiedades pueden expresarse en una sola expresión:

Si k₁ y k₂ son constantes (números reales) se verificará

[k₁·f(x)+k₂g(x)]´= k₁·f ´(x) + k₂·g´(x)

La tasa de variación media de y = k·f(x) resulta ser

Por tanto si h tiende a 0 entonces [k·f(a)]´ = k·f ´(a)

esta propiedad es válida para cualquier punto donde la función sea derivable, por tanto

[k·f(x)]´ = k·f ´(x)

Caso particular para k=-1

[-f(x)]´ = -f ´(x)

Ejemplo:

 Sea y = 3x², su derivada será

y´ = 3[x²]´= 3·(2x) = 6x

Si consideramos el intervalo [a,a+h] y calculamos los incrementos de las funciones dentro del intervalo, obtenemos:

s(a)=f(a)+g(a)

s(a+h)=f(a+h)+g(a+h)

s(a+h)-s(a)=f(a+h)+f(a+h)-f(a)-g(a)=f(a+h)-f(a)+g(a+h)-g(a)

La TVM de s(x) será:

suma de la TVM de f(x) más la TVM de g(x), y por tanto cuando h tiende a cero la expresión se convierte en

[f(a)+g(a)]´=f ´(a)+g´(a)

y generalizando para cualquier punto donde f y g sean derivables

[f(x)+g(x)]´=f ´(x)+g´(x)

Observación: teniendo en cuenta que f(x)-g(x) = f(x)+(-g(x) se deduce fácilmente que

[f(x)-g(x)]´=f ´(x)-g´(x)

Generalización al caso de una suma de más de dos funciones:

[f₁(x)+f₂(x)+....+f_n(x)]´=f₁´(x)+f₂´(x)+....+f_n´(x)

Calcular las derivadas de las funciones:

1.- x²+x

2.- 5x³-3x²-x+1

Demostrar:

Si dos funciones f(x), g(x) tienen la misma función derivada entonces aquellas difieren en una constante, es decir f(x) = g(x) + k

En efecto, supongamos que f ´(x) = g ´(x) entonces  f ´(x) - g ´(x) = 0

y teniendo en cuenta la propiedad de linealidad [f(x) - g(x)] ´ = 0. Este resultado significa que la función diferencia f(x) - g(x) = k (constante) o lo que es lo mismo f(x) = g(x) + k

CUADRO DE FUNCIONES DERIVADAS

Función	Derivada
Constante
y = k	y´= 0
Identidad
y = x	y´=1
Potenciales
y = xn	y ´= nxn-1
Exponenciales
Logarítmicas
Trigonométricas

Consideremos dos funciones f(x) y g(x), se cumple que

[f(x)g(x)]´ = f ´(x)g(x) + f(x)g´(x)

Ejemplo 1: 

D[x²lnx]=D[x²]lnx+x²D[lnx]=2xlnx+x²(1/x)=2xlnx+x

Ejemplo 2:

D[xsenx]=D[x]senx+xD[senx]=senx+xcosx

DERIVADA DEL COCIENTE DE DOS FUNCIONES

Consideremos dos funciones f(x) y g(x), g(x)¹0,se cumple que

Ejemplo1:

Ejemplo 2: