|
|
CONCEPTO
La
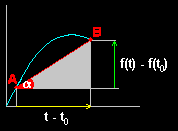
figura adjunta representa el movimiento de una bola lanzada
verticalmente hacia arriba desde el suelo. La altura y
es una función
del tiempo y=f(t)=50·t - 5·t2
Conviene que te
des cuenta que la trayectoria seguida por la bola es una recta vertical
mientras que la función altura-tiempo es una parábola y que no debes
confundir la gráfica de la función con la trayectoria. En la gráfica
altura-tiempo podemos calcular la altura si conocemos el tiempo. Pero
también podemos encontrar otro tipo de información, como por
ejemplo la rapidez del cambio de altura con el tiempo.
Si
aumentamos de forma continua el tiempo t verás
como la bola se eleva hasta alcanzar una altura máxima, después
desciende hasta llegar al suelo.
Para
estudiar el movimiento consideramos el instante inicial t0
y el instante final t
En el
tiempo trascurrido t - t0
segundos la altura ha variado f(t)-f(t0)
metros.
|
|
El
cociente
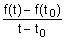
representa
el cambio experimentado por la altura en un segundo, es decir mide la
rapidez del cambio de altura y se denomina TASA DE VARIACIÓN MEDIA en
el intervalo [t0,t].
La TVM mide
la variación de la función relativa a un intervalo pero no nos informa
de cómo fue variando a lo largo del intervalo.
INTERPRETACIÓN
GEOMÉTRICA
La TVM
representa la pendiente de la recta que pasa por los puntos A
y B como
se puede apreciar en el triángulo rectángulo de la figura.
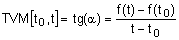
Como la
función y=f(t)
no es lineal resulta que la recta que pasa los puntos A
y
B
tiene distinta pendiente dependiendo del intervalo [t0,t]
que se esté considerando.
|
Experimenta:
-
Averigua
la altura máxima alcanzada.
-
Averigua
el tiempo que tarda en alcanzar la altura máxima.
-
Averigua
el tiempo que tarda en caer al suelo.
-
¿La
tasa de variación media TVM es la misma en cualquier intervalo de
tiempo?. Explica como va cambiando.
-
Calcula
la TVM en los siguientes intervalos [t0=0, t=1];
[t0=1, t=2]; [t0=2, t=4]; [t0=5,
t=7]
-
¿Qué
significa una TVM negativa?
-
Si
calculamos la TVM en un intervalo muy pequeño p.e [t0=2,
t=2,12] ¿que tal representaría la TVM a la velocidad que lleva la
bola en el instante t0=2 segundos?
-
Si
la TVM es nula ¿quiere decir que la función no ha variado a lo
largo del intervalo?. Explica esto.
-
Busca
dos instantes de tiempo t0 y t donde la bola esté a 80
metros del suelo. ¿Cuál es la TVM en este intervalo?
|
|
Cuando
se estudia la estatura de una persona se observa que su talla cambia
mucho entre los 6 y los 9 años, mientras que entre los 20 y 23 cambia
muy poco. La TVM de la talla de una persona es mayor en el primer caso
que en el segundo, pues en el mismo tiempo ha aumentado más su
estatura.
|
Cuando
se estudia la variación del número de nacimientos que se producen en
un país alo largo del tiempo, la TVM es la tasa de natalidad de la
población. |
