DERIVADA DE LA FUNCIÓN COMPUESTA

CONCEPTO DE FUNCIÓN COMPUESTA (función de función)

Sean las funciones  f(x) = x², g(x) = sen(x)

la función f  lo que hace es calcular el cuadrado f(1)=1²=1, f(2)=2²=4, etc. por tanto 

Recordar: (fog)(x)=f(g(x))

Regla de la cadena

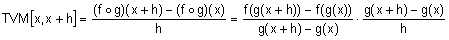
lo que significa, que si variamos x una cantidad h, obtenemos una variación g(x+h)-g(x) de la función g, a su vez como la función f depende de g, esta variación de g produce una variación en f: f(g(x+h)-f(g(x))

La tasa de variación media de g(x)  respecto de la variación de x es

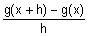
a la vez que la tasa de variación media de f(g(x)) respecto de la variación de g(x) es

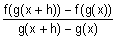
si pasamos al limite cuando x tiende a 0, también g(x+h)-g(x) tenderá a 0 por ser derivable (y por tanto continua) de lo que se deduce la siguiente regla de derivación de la función compuesta:

D_x[f(g(x))] = D_g[f(g(x)]·D_x[g(x)]

Este resultado se conoce como regla de la cadena donde la función g(x) hace de variable intermedia o de paso para derivar la función compuesta f o g respecto de la variable independiente x, que podemos expresar así:

"La derivada de (f o g)(x) respecto de x es igual al producto de la derivada de (f o g) respecto de g, por la derivada de g respecto de x".

Ejemplo1:

f(x) = sen (x²) es una función compuesta de la función potencial g(x)=x² y una trigonométrica f(g) = sen(g)

Por tanto

D_x[sen(x²)] = D_g[sen(g)]·D_x[g(x)] = cos(g)·2x =cos(x²)·2x = 2xcos(x²)

Visualización de funciones compuestas y de sus derivadas

Hay tres entradas de parámetros, función (1 a 10),  derivada (0,1) y a (abcisa del punto). El parámetro derivada puesto a 1 visualiza la expresión de la derivada y su gráfica correspondiente. La abcisa del punto permite evaluar la función y su derivada en dicha abcisa.

Para averiguar conocimiento que se tiene de las derivadas de las funciones compuestas, poner el parámetro derivada a valor 0 y seleccionar una función de 1 a 10, después reemplazar la entrada editable g(x) por la supuesta función derivada y poner el parámetro derivada a 1 para comprobar si la entrada de la función derivada ha sido correcta.

Pulsar Inicio y repetir para otra función.

Pulsando Inicio y poniendo el parámetro función a 0, se podrá introducir la entrada f(x) y g(x) por las funciones que el estudiante desee, aunque en este caso el programa no comprueba si la entrada de la función derivada es correcto.

1: Calcula la derivada de cada una de las funciones siguientes:

2: Sea la función f(x)=4e^{-x^2} (*)

a) Calcular el punto (a,f(a)) de la curva  donde el valor de la función coincide con el de su derivada. 

b) Calcular el punto (a, f(a)) donde la tangente a la curva tiene una inclinación de 45º. Obtener la ecuación de dicha tangente.

3: Una empresa textil produce tejidos de algodón. El coste de fabricación (en miles de euros) depende de la cantidad fabricada (en metros cuadrados) según la función C(x)=20.000+20ln(1+0.5x)

a) Calcula la derivada de la función de costes y su valor en x=20.000m².

(Nota: en economía, se llama función de costes marginales a la derivada de la función de costes).

b) Si la empresa produce 20.000 m² de tela, ¿cuánto le costaría producir un m² adicional? Compara este resultado con el valor del coste marginal para x=20.000

Soluciones

 Algunas expresiones que admite el programa para las funciones f(x) y g(x) son: