I  Integral definida como límite de sumas superiores e inferiores.

Si hacemos tender n (número de puntos de la partición) hacia infinito, o lo que es lo mismo las bases de los rectángulos hacia cero, podremos calcular el límite tanto de las sumas superiores de Riemann como de las sumas inferiores.

Si existen ambos límites y son iguales diremos que la función f es integrable y definiremos la integral definida entre a y b de f como el resultado de este límite, es decir

• A los extremos del intervalo a y b se les llama límite inferior y superior de integración, respectivamente
• La función f recibe el nombre de integrando

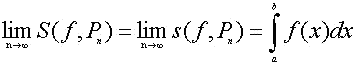
1.- Observa la siguiente escena. Modificando el parámetro "opción" aparecerán diferentes funciones. Todas son constantes aunque no necesariamente positivas.
Compara el valor del área del recinto con la integral definida en ese intervalo. ¿Podemos decir que ambos conceptos son iguales?. ( Los rectángulos verdes que aparezcan se pueden trasladar si los arrastramos de su vértice  izquierdo señalado con un punto rosa)

2.- Observa la opción 2 y compara con tus apreciaciones de la opción 1.

3.- Y ¿Qué ocurre en cada opción si se escogen los valores b<a?

4.- Analiza la definición de integral definida e intenta dar una explicación a estos hechos.

5.- Determina la relación entre el área del recinto mixtilíneo y la integral definida para funciones negativas.

6.- ¿Podría darse el caso de un recinto mixtilíneo cuya superficie sea no nula y su integral definida valga 0?. Pon ejemplos.

7.- Establece la relación entre el signo de la función y el signo de la integral definida de esa función.

           Propiedad 1: Sea c un punto interior al intervalo [a,b]. Observa la relación entre las áreas rosa y naranja.

8.- Relaciona la integral de una función entre a y b , con las integrales de la misma función entre [a,c] y [c,b].

9.- ¿Se puede generalizar el resultado para funciones que nos sean necesariamente positivas?

10.- Deduce la siguiente propiedad: Si c en un punto interior al intervalo [a,b], entonces

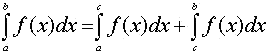
11.- Deduce cuál será la integral definida de una función si a=b. Comprueba tus resultados en la siguiente escena

12.- Demuestra analíticamente el resultado.

13.- ¿Se podrá afirmar que si b1<b2 entonces la integral entre a y b1 es menor que la integral entre a y b2?.  ¿En qué condiciones esta afirmación es cierta?

14.- Y en el caso de dos funciones distintas f₁ y f₂ , de manera que  f₁<f₂, entonces ¿La integral entre a y b de f₁ es menor que la integral entre a y b de f₂?.

       Propiedad 3: Si se permutan los límites de integración la integral cambia de signo, es decir

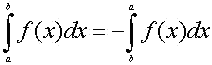
15.- Deduce esta propiedad de los resultados obtenidos en el ejercicio 1.

16.- Utilizando las propiedades 1 y 2, demuestra analíticamente este resultado

        Propiedad 4: Integral de la suma o diferencia de dos funciones
 

11.- Deduce las fórmulas de la funciones f (verde) y g (roja) en cada escena. Determina la función suma y diferencia respectivamente (Si modificas el punto x0 obtendrás el resultado (gráfica turquesa). Observa la relación entre los rectángulos que se pueden formar bajo su gráfica (Estos rectángulos se pueden desplazar arrastrándolos de su vértice inferior izquierdo). Enuncia la relación que hay entre las integrales de f, g y su suma f+g. ¿Es el resultado extensible a la diferencia?

12.- ¿Qué relación habrá entre la integral de una función y la integral del doble de esa función. Generaliza al producto por un número real

        Propiedad 5: Teorema de la media.

13.- Observa la elección de los rectángulos en cada partición y el resultado de las áreas gris y naranja. ¿Qué es lo que ocurre?. ¿Por qué?

14.- Deduce la relación que hay entre los rectángulos elegidos en esta escena y los elegidos cuando se hace la aproximación por exceso y defecto. Cuando n=1 compara las áreas de los tres. Ten en cuenta que los nuevos rectángulos tienen el área del trapecio mixtilíneo.

15.- De las desigualdades obtenidas en el ejercicos anterior deduce la siguiente

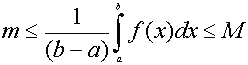
con m y M el mínimo y máximo respectivamente de f en [a,b].

16.- Aplica el teorema del valor medio a la función continua f y deduce el siguiente teorema de la media

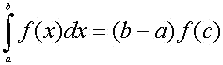
donde c es un punto intermedio fijo de [a,b]. El valor f(c) recibe el nombre de altura media o valor medio.
L

        Propiedad 6: Relación entre el valor absoluto de la integral y la integral del valor absoluto de una función. (Si modificas la opción podrás ver los resultados)

17.- ¿En qué casos el valor absoluto de la integral coincide con la integral del valor absoluto?

	Ministerio de Educación, Cultura y Deporte. Año 2001