area

CÁLCULO INTEGRAL

El problema del cálculo de áreas

I El área bajo una curva.

Dada una región del plano, su área puede aproximarse por medio de regiones poligonales inscritas o circunscritas a la misma. Este procedimiento llamado exhaución ya era conocido por los griegos.

Estamos interesados en calcular el área del recinto amarillo (llamado trapecio mixtilíneo), limitado por una curva (gráfica de una función continua), el eje de abscisas y las rectas verticales x=a y x=b, con a y b dos valores reales. Arquímedes (287-212 a.C.) ya obtuvo resultados importantes como el cálculo del área encerrada por un segmento parabólico.

1.- Observa el siguiente trapecio mixtilíneo. Si tuvieras que elegir un polígono para aproximar el área del recinto naranja ¿cuál elegirías?. ¿Por qué?. (Si aumentas el valor de n a 1 verás nuestra propuesta)

2.- Una vez dado el este paso ¿Qué harías para mejorar nuestra primera aproximación? (Podrás ver una solución si aumentas de nuevo el valor de n)

Cuantos más rectángulos construyamos mejor será la aproximación. El proceso llevado a cabo es el siguiente:

Al intervalo [a,b] se le subdivide en subintervalos que forman las bases de los rectángulos.
Al realizar la subdivisión del intervalo aparece un conjunto de números reales ordenado y finito

₀

, x

₁

, x

₂

, x

₃

...,x

} que se llama partición del segmento [a,b].

Cada partición compuesta por n+1 puntos determina n rectángulos. En nuestro caso las bases tienen la misma longitud, aunque en general no es necesario.
Se obtienen los rectángulos inscritos dentro del recinto mixtilíneo, su calculan sus áreas y se obtiene la suma final.

3.- Calcula la superficie del área gris, para sucesivas particiones del intervalo [a,b]. En la escena de la derecha hallarás las soluciones. (El punto azul te puede ayudar a calcular las alturas de los rectángulos)

4.- ¿Cómo se selecciona el valor de la altura de los rectángulos?. ¿Seguirá el mismo criterio en todas las regiones?. A continuación te proponemos otro trapecio mixtilíneo. Repite el proceso y extrae conclusiones

5.- Deduce otras posibilidades, siguiendo la misma técnica, para aproximar el área del recinto amarillo utilizando rectángulos u otras figuras que te parezcan más adecuadas. Analiza las ventajas e inconvenientes de cada sistema.

De la misma forma que hemos actuado hasta ahora, podíamos haber elegido los rectángulos cuya superficie fuese mayor que la del recinto naranja. A este procedo se le llama una aproximación por exceso.

Los trapecios aproximan mejor que los rectángulos pero su fórmula para calcular el área es un poco más complicada. El proceso seguido en esta escena es lo que se denomina la fórmula de cuadratura de los trapecios compuesta. Cuando se necesita una aproximación del área se suele utilizar. Su uso lo estudia una rama de las matemáticas llamada cálculo numérico y tiene su importancia porque estas fórmulas son implementables en un ordenador.

6.- Calcula las sucesivas áreas de las zonas grises para cada partición.

7.- Escribe como sería la fórmula general que permita calcular un área mediante la regla de los trapecios compuesta

8.- ¿Cuántos veces tendremos que hacer el proceso para obtener el área del recinto?

9.- ¿Cómo evolucionan las superficies grises cuando hacemos más fina la partición?

En el caso que aproximemos por defecto el área del recinto mixtilíneo mediante rectángulos, para cada partición fija P={x₀, x₁, x₂, x₃...,x_n}, se elige como altura del rectángulo de base el subintervalo [x_i-1,x_i], el mínimo del valor del función en ese subintervalo y que notaremos por m_i. Si la aproximación es por exceso elegiremos el máximo de la función en ese subintervalo y lo llamaremos M_i.

10.- Compara estas afirmaciones con tus respuestas en la actividad 4.

11.- Obtén una fórmula compacta que calcule el área de las zonas grises correspondientes para una partición prefijada.

Se llama suma superior de Riemann de f asociada a la partición P a

y se llama suma inferior de Riemann de f asociada a la partición P a

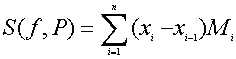
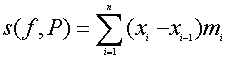
12.- Interpreta el significado de estas fórmulas.

13.- Si la base de los rectángulos es cada vez más pequeña ¿Cómo evolucionarán estas sumas?

Autor: Enrique Martínez Arcos


	Ministerio de Educación, Cultura y Deporte. Año 2001