
Ya hemos visto que conociendo la función derivada de una función podemos recuperar la función original a la que hemos llamado función primitiva.
1.- Si modificamos el valor de la constante C ¿Qué obtendremos?. Recuerda como afecta a la gráfica de una función sumar o restar una cantidad fija a su fórmula.
2.- Observa la relación entre las funciones que se obtienen y la función derivada de cada una de ellas. ¿Esto es coherente con las reglas de derivación?.
3.- En estas condiciones qué respuesta podemos dar a las siguientes cuestiones:
Si hay más de una primitiva de la misma función y=f(x), cada una de ellas estará determinada por un punto por el que pase la gráfica de esa función
5.- Elige una punto P cualquiera del plano. (Sus coordenadas (P.x,P.y) pueden ser modificadas bien con las flechas o escribiendo directamente las nuevas coordenadas en su correspondiente ventana). Observa la primitiva que se obtiene. Vuelve a replantear el ejercicio 3 apartado 2.
II Integral indefinida.
Se llama integral indefinida de una función y=f(x) al conjunto de todas las primitivas de f. A la integral indefinida de la función f se le nota por la expresión
![]()
y se lee integral de f diferencial de x. Al símbolo que inicia la expresión (y que tiene forma de s alargada) se le llama signo integral y lo que le sigue integrando.
6.- Calcula la integral indefinida de la función constante f(x)=0
7.- Demuestra el siguiente resultado: Dadas dos primitivas F y G de una función f, entonces la diferencia entre F y G es una constante. (Demuestra que la función F-G es una primitiva de la función 0 y utiliza el ejercicio 6)
De este resultado se puede deducir un procedimiento para calcular la integral indefinida de una función. Basta con calcular una primitiva y la integral indefinida será la familia de funciones que resulte de sumar a esa primitiva una constante.
![]()
donde F(x) es una primitiva de f(x). A la constante C se le denomina constante de integración.
III Propiedades de linealidad de la integral indefinida.
De las reglas de derivación que afectan a las cuatro operaciones fundamentales, dos, la derivada de una suma (o diferencia) es la suma (o diferencia) de las derivadas de dichas funciones, y la derivada de un número real por una función es igual a número real por la derivada de la función, nos van a proporcionar propiedades de linealidad de la integral indefinida, de forma inmediata.
8.- Demuestra que "La integral indefinida de la suma (o resta) de dos funciones es la suma (o resta) de las integrales indefinidas de cada una de las funciones".
![]()
9.- Demuestra que "La integral indefinida del producto de un número real l por una función es el producto del número real l por la integral indefinida de la función.
![]()
IV Cálculo elemental de integrales indefinidas.
Conociendo la relación entre derivación
e integración y utilizando estas dos propiedades podemos calcular
integrales indefinidas de algunas funciones elementales.
| Gracias a las reglas de derivación
sabemos calcular la función derivada de algunas funciones. Así
por ejemplo
|
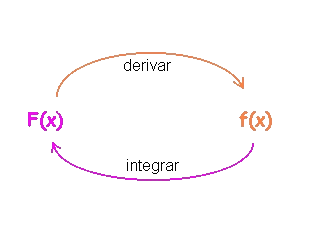 |
Si queremos calcular la integral de una
función f(x), la estrategia pasa por
pensar qué función F(x) tiene
por derivada la función original.
|
|
|
||
Además las dos propiedades de linealidad nos permitirán tranformar en inmediatas algunas integrales, por ejemplo:
![]()
o bien
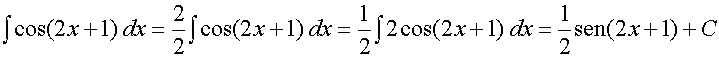
10.- Calcula las integrales indefinidas
de las siguientes funciones
| f1(x)=2/x2 | f2(x)=5e2x | f3(x)=3/(2x+8) | f4(x)=cos(1-x)/2 | f5(x)=x1/2/7 |
| f6(x)=5x2-2x+5 | f7(x)=x/(1+x) | f8(x)=7/cos2(x) | f9(x)=5+5tg2(x) | f10(x)=e-x+cos(3x) |
Para obtener las primitivas arrastra el punto x0. Cada escena calcula la primitiva específica que pasa por el punto P. arrastrando de este punto se pueden obtener el resto de primitivas que completan la integral indefinida.
|
|
|
|
|
|
||
|
|
|
|
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||