
Dos caminos que han ido separados
a lo largo de la historia de las matemáticas, tras más de
20 siglos, se unen, en lo que englobaremos como cálculo integral,
gracias a los trabajos de Barrow, Newton y Leibniz (creadores del cálculo
infinitesimal).
Uno de los caminos, la búsqueda
de fórmulas que permitieran calcular la superficie de recintos planos,
se remonta a los matemáticos griegos.
El otro camino nace para dar continuidad
al concepto de derivada, buscando una operación recíproca.
Comencemos por aquí.
I Función derivada.
Ya conoces el concepto de derivada de una función en un punto como el siguiente límite
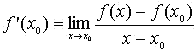 o equivalentemente
o equivalentemente![]()
si llamamos h a la diferencia x-x0.
Si una función y=F(x) es derivable en su dominio, es posible definir una nueva función, que llamaremos función derivada y que representaremos por y=F'(x), que asocie a cada número real del dominio x0 la derivada de la función F en ese punto x0.
1.- ¿Qué representa la derivada de una función en un punto?. Qué interpretación geométrica tiene?.
2.- ¿Que indica la pendiente de una recta?. ¿Cómo se calcula?
Para calcular la función derivada no hace falta obtener los límites ya que para las funciones elementales disponemos de unas reglas de derivación.
3.- Calcula la fórmula de la función derivada de la función F(x)=0.25x2-3 utilizando las reglas de derivación.
4.- Calcula los valores de F'(-1), F'(0) y F'(2) utilizando la definición como límite. Compara con los procedimientos obtenidos con anterioridad.
5.- Calcula la fórmula de la función derivada de la función F(x)=0.25x2-3 utilizando la definición de función derivada en un punto, para cualquier punto genérico x del dominio.
II El problema recíproco.
Dada una función y=f(x), se busca otra función F cuya derivada sea f. Es decir F'(x)=f(x). A esta función F se le llama primitiva de la función f.
6.- Observa como las rectas tangentes a una curva determinan la propia curva. (Modifica el valor de x0 utilizando las flechas). Compara los resultados obtenidos con la escena anterior.
| Ministerio de Educación, Cultura y Deporte. Año 2001 | ||