|
MOVEMENTOS NO PLANO |
| Vectores | |
| 1. DEFINICIÓN DE VECTOR | |
|
|
Adaptación e tradución dunha escena de Miguel García Reyes |
1.- Arrastra os puntos P e Q e crea diferentes vectores ao longo de toda a escena. 2.- Sitúa o punto P no (0,0) e o punto Q no ( 0, 4). Poderías dicir cal é o módulo do vector? 3.- Sitúa agora o punto Q no (3, 4) mantendo P na orixe de coordenadas. Como podes calcular o módulo do vector? |
2. Coordenadas dun vector |
|
Dados dous puntos calquera A e B de coordenadas (a1,a2) e (b1,b2) respectivamente, as coordenadas do vector
|
|
Adaptación e tradución dunha escena de Miguel García Reyes |
1.- Na escena podes observar un vector de orixe P (0,0) e extremo Q (3,2). Xoga cos controis q.x e q.y e observa como o punto Q se move ao longo da escena. Fíxate no feito de que as coordenadas de Q coinciden coa do vector: a que se debe? 2.- Move agora o punto orixe ao (1, 2). Xoga de novo cos controis q.x e q.y e observa que, como diciamos anteriormente, as coordenadas do vector obtéñense restando as do extremo coas da orixe. 3.- Repite o proceso movendo a orixe ao (-1, -2).
|
|
|
4.- Na escena que tes á esquerda aparece un vector. No teu caderno indica as coordenadas da orixe e as coordenadas do extremo e calcula as coordenadas do vector. 5.- Pulsa o botón Inicio e aparecerá un novo vector. Repite o proceso ata seis veces. |
Adaptación e tradución dunha escena de Miguel García Reyes |
|
3. VECTORES EQUIPOLENTES |
|
Consideremos un vector calquera V coa súa dirección, o seu sentido e o seu módulo. Calquer outro vector que sexa paralelo a V e que teña o mesmo sentido e módulo, dise que é equipolente a V. Na seguinte escena Descartes, poderás construir vectores equipolentes dun xeito sinxelo e intuitivo. |
|
Adaptación e tradución dunha escena de Miguel García Reyes |
1.- Arrastra co rato a orixe do vector e móveo por toda a escena. Fíxate que mantemos sempre a mesma dirección, o mesmo sentido e o mesmo módulo (de feito, as coordenadas do vector non cambian). En consecuencia, tras cada movemento que fagamos teremos un vector equipolente ao inicial.
2.- Indica no teu caderno as coordenadas dos puntos orixe e extremo de catro vectores equipolentes ao inicial e que estean, cada un deles, nun cadrante distinto. 3.- Modifica as coordenadas do vector 4.- Consideremos os puntos A(0,-1) e B(4,-2). Calcula no teu caderno as coordenadas do vector |
4. Suma de vectores libres |
||
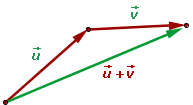
Dados dous vectores u e v, o vector suma u + v non é máis que aquel que se constrúe facendo coincidir o extremo do primeiro coa orixe do segundo. A nivel de coordenadas, bastará con sumar as coordenadas de cada un dos vectores u + v = ( u1 + v1 , u2 + v2 ) |
 |
|
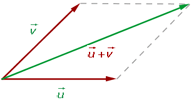
Para realizar a suma dun xeito máis sinxelo, podemos empregar a denominada regra do paralelogramo.
Consiste en tomar representantes dos vectores coa orixe en común, trazar rectas paralelas aos vectores obtendo un paralelogramo cuxa diagonal coincida coa suma dos vectores. Na seguintes escena, aplicaremos esta regra para calcular o vector suma. |
 |
|
Adaptación e tradución dunha escena de Miguel García Reyes
|
1.- Calcula a suma dos vectores U= (3,-2) y V= (1,3). Acha as coordenadas do vector suma e comproba o resultado na escena Descartes. 2.- Repite a operación cos vectores U= (-1,3) y V= (1,-3). Que acontece neste caso? 3.- Usando a escena Descartes, averigua as coordenadas do vector V sabendo que U= (2,5) e U + V= (3,2) |
|
 |
 |
 |
||||
 |
| Xosé Anxo Fernández Alonso | ||
 |
||
| © Ministerio de Educación, Política Social y Deporte. Año 2009 | ||
ten orixe en A e extremo en B mentras que o vector 
ten orixe en B e extremo en A.
ata que sexan (-1,4). Coa axuda de Descartes, indica cal sería o extremo de cada un dos vectores equipolentes ao indicado que teñen por punto orixe (2,-2), (0,-1) e (-2,-3) respectivamente.