
 |
Límites y Continuidad |
| Análisis | |
| B) FUNCIÓN A TROZOS CON UN SALTO EN EL PUNTO | ||||||
Vamos
a estudiar el comportamiento de la función 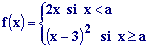 en las proximidades de
x=a
en las proximidades de
x=a
En el inicio de la escena es a=1. También tenemos un punto P de la función, cuya abscisa x podemos variar en los botones inferiores. |
||||||
| Para
valores de x menores que a (izquierda de
a), la gráfica es
una recta que llega hasta el punto (a,2a), en el inicio
(1,2), aunque este punto no pertenece a la función
(hueco),
ya que en la definición de la función f(x)=2x para
x<a,
pero no para x=a.
Partiendo del inicio (a=1), haz una tabla de valores en tu cuaderno dando a x los valores -1, -0.75, -0.5, -0.25, 0, 0.25, 0.5, 0.75 observando en la escena los valores de la función y hacia donde se dirige el punto P. Deduce a qué tiende la función (valores de y) cuando x tiende a 1 por la izquierda (x<1). Para valores
mayores que a (derecha de a), la gráfica es parte
de una parábola que comienza en el punto (a,(a-3)2).
En el
inicio este punto es (1,4), que ahora sí pertenece a la función, pues en la
definición de la misma indica x |
||||||
|
EXERCICI 10.-Partint del inici (INICI) fes una taula de valors en el teu full d'activitats donant a x els valors 2 (limpiar), 1.75, 1.5, 1.25, 1 observant en la escena els valors de la funció i fins a on es dirigeix el punt P. Dedueix a què tendeix la funció (valors de y)quan x tendeix a 1 per la dret (x>1) Después de haber hecho el ejercicio tienes que llegar a la siguiente conclusión suponiendo a=1:
Por tanto al no coincidir el límite por la derecha y por la
izquierda, no existe el límite de la función cuando x Esta función no es
continua en x=a porque no existe el límite Comprueba en la escena anterior que ocurre lo mismo para otros valores de a. |
||||||
| C) FUNCIÓN RACIONAL QUE LE FALTA EL PUNTO | ||||||
Vamos
a estudiar el comportamiento de la función 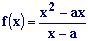 en las proximidades de
x=a
en las proximidades de
x=aEn el inicio de la escena es a=2. También tenemos un punto P de la función, cuya abscisa x podemos variar en los botones inferiores. |
||||||
|
Para
valores de x menores que a (izquierda de
a), la gráfica es
una recta que llega hasta el punto (a,a), en el inicio
(2,2), aunque este punto no pertenece a la función
(hueco),
ya que para x=a, tendremos EXERCICI 11.- Partint del inici (INICI) fes una taula de valors en el teu full d'activitats donant a x els valors 1, 1.2, 1.4, 1.6, 1.8 observant en la escena els valors de la funció i fins a on es dirigeix el punt P. Dedueix a què tendeix la funció (valors de y)quan x tendeix a 2 per la esquerra (x<2) Para
valores mayores que a (derecha de a), la gráfica es una recta
que comienza en el punto (a,a), en el inicio (2,2), que
ya hemos dicho que no pertenece a la función (hueco), ya que para
x=a, tendremos EXERCICI 12.- Partint del inici (INICI) fes una taula de valors en el teu full d'activitats donant a x els valors 3 (limpiar), 2.8, 2.6, 2.4, 2.2 observant en la escena els valors de la funció i fins a on es dirigeix el punt P. |
||||||
|
Deduce a qué tiende la función (valores de y) cuando x tiende a 2 por la derecha (x>2). Después de haber hecho el ejercicio tienes que llegar a la siguiente conclusión suponiendo a=2:
Por tanto al coincidir el límite por la derecha y por la izquierda,
existe el límite de la función cuando x Esta función no es
continua en x=a porque no está definida
en x=a, ya que |
||||||
| D) FUNCIÓN A TROZOS CON EL PUNTO DESPLAZADO | ||||||
Vamos
a estudiar el comportamiento de la función 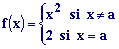 en las proximidades de x=a
en las proximidades de x=aEn el inicio de la escena es a=2. También tenemos un punto P de la función, cuya abscisa x podemos variar en los botones inferiores. |
||||||
Para valores de x menores que a (izquierda de a), y también para valores de x mayores que a (derecha de a), la gráfica es una parábola que se interrumpe en x=a (hueco). El punto
que falta tendría de coordenadas (a,a2), en el
inicio de la escena (2,4), pero para x=a
f(a)=2, según
nos dice la definición de la función. EXERCICI 13.- Partint del inici (a=2) fes una taula de valors en el teu full d'activitats donant a x els valors 1, 1.25, 1.5, 1.75 observant en la escena els valors de la funció i fins a on es dirigeix el punt P.
|
||||||
EXERCICI 14.- Partint del inici (a=2) fes una taula de valors en el teu full d'activitats donant a x els valors 3 (limpiar), 2.75, 2.5, 2.25 observant en la escena els valors de la funció i fins a on es dirigeix el punt P. Deduce a qué tiende la función (valores de y) cuando x tiende a 2 por la derecha (x>2). Después de haber hecho el ejercicio tienes que llegar a la siguiente conclusión, suponiendo a=2:
Por tanto al
coincidir el límite por la derecha y por la izquierda, existe el límite
de la función cuando x La función está
definida en x=2 pero f(2)=2, no coincide con el límite. En general la
función está definida en x=a pero f(a) Comprueba en la escena anterior que ocurre lo mismo para otros valores de a. |
||||||
4.-
Relación
de la continuidad en a
con el límite cuando x
|
||||||||||||
| Si observas las cuatro funciones anteriores, discontinuas en x=a, deducimos que para que una función sea continua en un punto debe cumplirse lo siguiente: | ||||||||||||
|
||||||||||||
 |
 |
 |
||||
|
Original de Ángela
Núñez Castaín Modificat per Eva Lindo |
||
 |
||
| © Ministerio de Educación. Año 2001 | ||

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.