Dominio_definicion_funcion_2

	DOMINIO DE DEFINICIÓN DE UNA FUNCIÓN_2
	Análisis

1.3.- CÁLCULO DEL DOMINIO DE funciones racionales

Para el cálculo del dominio de las funciones con la x en el denominador o racionales, hay que tener en cuenta que el denominador de una fracción nunca puede ser nulo.
Luego los valores de x que hagan cero el denominador de la función no pueden pertenecer al dominio de la misma

A) En esta escena se representan las funciones racionales del tipo

(en verde), y la recta del denominador y=cx+d (en rojo oscuro).

Podemos cambiar los valores de a, b, c y d para obtener distintas funciones del mismo tipo.

También tenemos un punto P, del cuál podemos ver en la escena sus coordenadas, y cambiar su abcisa, x, en el botón inferior.

Para averiguar qué punto no pertenece a la función se hace el denominador cx+d=0, de donde x=-d/c . Vemos que es el punto donde la recta del denominador corta al eje X.
Es el punto señalado en rojo en la escena, y es el que no pertenece al dominio de la función racional.

Así en el inicio de la escena está representada la función donde el denominador es cero para x = -3. Por tanto el dominio de esta función es
D = R - {-3}. Esto es, todos los números reales quitando el -3

Prueba a introducir en la escena el valor de x=-3 y observa lo que ocurre.

EXERCICI 5.- Troba en el teu full d'activitats el domini de les següents funcions, comprovant els teus resultats en la escena anterior:

a) b)

B) Si el denominador de la fracción es de segundo grado, puede haber hasta dos puntos que anulen el denominador. En dichos puntos no existirá la función, y el dominio serán todos los números reales quitando los valores de x que hacen cero el denominador.

Por tanto lo primero que hay que hacer para hallar el dominio es igualar a cero el denominador y resolver la ecuación resultante.

Veámoslo gráficamente:
En esta escena tenemos representadas funciones racionales (en verde) cuyo denominador es un polinomio de segundo grado ax²+bx+c (en rojo oscuro).

Los coeficientes a, b y c podemos cambiarlos con los botones inferiores y así obtener distintas funciones del mismo tipo.

Los puntos marcados en rojo son los que hacen cero el denominador, y por tanto donde no existe la función racional.

También podemos ver un punto P de la función racional y sus coordenadas.

Prueba a dar los valores que anulan el denominador a la abscisa del punto P, x, en la parte inferior de la escena, y observa lo que ocurre.

En el inicio de la escena aparece la función
Si se iguala a cero el denominador x²-4x+3=0, obtenemos dos soluciones: x=1, x=3, donde corta la parábola (y=x²-4x+3) al eje X.
Podemos ver en la escena que justamente en esos puntos es donde no existe la función racional.

Por tanto el

DOMINIO de la función

es

D=R-{1,3}

Nota: La expresión entre llaves {1,3} sólo incluye a los valores de x aislados, 1 y 3. No confundir con [1,3] que indica el intervalo cerrado [1,3], o sea todos los valores de x entre 1 y 3, incluidos 1 y 3. Si escribimos (1,3) sería también un intervalo, pero abierto, serían todos los valores de x entre 1 y 3, pero no están incluidos ni el 1 ni el 3.

EXERCICI 6.- Troba en el teu full d'activitats el domini de les següents funcions, comprovant els teus resultats en la escena anterior:

a)	b)	c)
d)	e)

1.4.- Cálculo del dominio de funciones con raíces en el denominador

A) En esta escena tenemos representadas funciones del tipo

, junto con la función que aparece dentro de la raíz del denominador, o sea la función y=ax+b (en rojo oscuro).
Cuando esta función polinómica es negativa, no existe la raíz, tampoco el denominador y tampoco la función

Cuando la función polinómica es cero, existe la raíz, que será cero, pero al ser cero el denominador, no existe la función

Hemos señalado en rojo el punto que hace cero el denominador, donde la recta y=ax+b corta al eje X, y sombreado en gris la parte negativa de dicha recta.

Por tanto en el punto rojo y en el intervalo sombreado no existe la función
como puede verse en la escena

Dando a la abscisa del punto P, x, un valor dentro del dominio podemos observar la ordenada del punto. Observa qué ocurre cuando le das a x un valor fuera del dominio de la función.

Para hallar analíticamente el dominio de la función

, hay que averiguar cuándo la función polinómica y=ax+b es positiva, esto es resolver la inecuación ax+b>0 . (Puedes recordar como se hace en el punto 1.1.2 de esta lección)

En el inicio de la escena la función que aparece es .

Para hallar su dominio analíticamente hacemos x-1 >0, de donde x >1. DOMINIO=(1,¥)
(Ahora ponemos paréntesis en el intervalo, pues en x=1 no existe la función, si no sería cero el denominador).

Para hallar el dominio gráficamente basta representar la función polinómica y=ax+b y ver el intervalo donde esta función es positiva, pues ese intervalo será el dominio de la función
En el caso de la función , basta observar en el inicio de la escena que el intervalo donde y=x-1 es positiva es a la derecha de x=1. Por tanto el domino es (1,)

EXERCICI 7.- Troba en el teu full d'activitats el domini de les següents funcions, comprovant els teus resultats en la escena anterior:

a)

b)

B) En esta escena tenemos representadas funciones del tipo , junto con la función que aparece dentro de la raíz del denominador, o sea la función y=ax²+bx+c

Cuando esta función polinómica es negativa, no existe la raíz, tampoco el denominador y tampoco la función
Cuando la función polinómica es cero, existe la raíz, que será cero, pero al ser cero el denominador, no existe la función .

El punto P es un punto de la función racional, del cuál puedes ver sus coordenadas, y puedes moverlo cambiando su valor de x.

Hemos señalado en rojo los puntos que hacen cero el denominador, y sombreado en gris la parte negativa de la función y=ax²+bx+c
Por tanto en los dos puntos rojos y en el intervalo sombreado no existe la función

como puede verse en la escena.

Observa lo que ocurre cuando le das a x un valor fuera de su dominio.

Por tanto para hallar analíticamente el dominio de la función

hay que estudiar el signo de la función polinómica y=ax²+bx+c . (Puedes recordar como se hace en el punto 1.2 de esta lección)

Para hacerlo gráficamente basta representar la función polinómica y=ax²+bx+c y ver los intervalos donde esta función es positiva, pues esos intervalos serán el DOMINIO de la función

En el inicio de la escena podemos ver que el dominio de la función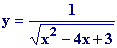

es (-,1) U (3,)

EXERCICI 8.- Troba en el teu full d'activitats el domini de les següents funcions, comprovant els teus resultats en la escena anterior:

a)	b)	c)
d)	e)

CONCLUSIONES

RAZONES POR LAS QUE EL DOMINIO DE DEFINICIÓN DE UNA FUNCIÓN PUEDE RESTRINGIRSE

EJEMPLOS

Imposibilidad de realizar alguna operación con ciertos valores de x:

Denominadores que se anulan	no está definida en x=-3 porque ahí se anula el denominador: D=R-{-3}
Raíces cuadradas de números negativos	no está definida para valores de x menores que 1 que darían raíces de números negativos: D=[1,)
Denominadores que se anulan y raíces de números negativos	no está definida para valores de x comprendidos entre 1 y 3 que darían raíces de números negativos, ni para 1 ni para 3, que harían el denominador cero: D= (-,1) U (3,)

Contexto real del que se ha extraído la función

V=a³ es el volumen de un cubo de arista a. La función no está definida para a nulo o negativo: D=(0,)

Por voluntad de quien propone la función

y=2x+5; x

[1,4]
D=[1,4] porque así lo deseamos

Funciones a trozos

no está definida para x=2
D=R-{2}

Por la naturaleza de la función:

Funciones trigonométricas	y=tag(x) no está definida en x=p/2+2kp D=R-{p/2+2kp}
Funciones logarítmicas	y=ln(x) no está definida para x=0 ni para x<0 D=(0,)

	Original de Ángela Núñez Castaín Modificat per Eva Lindo

	© Ministerio de Educación. Año 2001

Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.