a)Existeix la funció y = x²+ 8x+15 per a qualsevol valor de x? 

b) Què passa quan li dones a x (Q.x) un valor negatiu en la funció ? 

Existeix aquesta funció per a qualsevol valor de x? 

Habrás podido deducir del ejercicio anterior que la función polinómica y = x² + 8x + 15 existe para cualquier valor de x, o sea podemos dar a x un valor cualquiera y siempre se obtendrá un valor real de y. Decimos que esta función está definida en todo R (números reales) o bien su dominio de definición es R o (-∞,∞).
Sin embargo la función y =  no existe cuando x es negativo, no podemos dar a x valores negativos. Su dominio de definición es [0,∞).

PRIMERA CONCLUSIÓN:
Las funciones polinómicas tienen Dom f(x)=R
Las funciones con raíces cuadradas, o de índice par, no existen cuando el radicando es negativo.

En esta escena está representada la función , y la función que aparece en el radicando, o sea debajo de la raíz, y = ax +b

ax+b≥ 0	y=ax+b positiva		gráfica de y=ax+b encima eje X		EXISTE
	ax+b nº positivo		es nº real
ax+b<0	y=ax+b negativa		gráfica de y=ax+b debajo eje X		NO EXISTE
	ax+b nº negativo		no es nº real

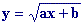
Prueba distintos valores de a y b, que originarán distintas funciones del tipo , e intenta adivinar para qué valores de x existe la función
Esos valores de x son el DOMINIO  de la función

Por ejemplo en el inicio de esta escena vemos que el DOMINIO de la función es D = [1, ∞)  
(ponemos un corchete en el 1 para indicar que 1 pertenece al dominio, o sea que la función existe para x=1)

Y si das los valores a=-3 y b=5, verás que el DOMINIO de la función   es Dom y = (-∞, 5/3]

Analíticamente para hallar el DOMINIO de la función , se resuelve la inecuación ax+b0, de donde se deduce el DOMINIO .

Y para hallar el dominio  de la función  así: -3x + 5 ≥ 0  -3x  - 5   3x  5  x 5/3 a partir de 5/3 hacia la izquierda Dom y = (-∞, 5/3]

EXERCICI 2.- Calcula analíticament en el teu full d'activitats  el DOMINI  de les següents funcions, comprovant els teus resultats en la escena anterior:
a)         b) 

En esta escena está representada la función , y la función que aparece en el radicando, o sea debajo de la raíz,

y = ax² +bx+c

ax2+bx+c 0	y=ax2+bx+c positiva		gráfica de y=ax2+bx+c encima eje X		EXISTE
	ax2+bx+c nºpositivo		es nº real
ax2+bx+c<0	y=ax2+bx+c negativa		gráfica de y=ax2+bx+c  debajo eje X		NO EXISTE
	ax2+bx+c nºnegativo		no es nº real

Fíjate bien en los valores de x que hacen que la función y=ax²+bx+c esté por encima del eje X. Para esos valores de x (dominio) existe la función  .

Prueba distintos valores de a, b y c que originarán distintas funciones  e intenta adivinar para qué valores de x existe la función  
Esos valores de x son el dominio de la función  .
Por EJEMPLO en el inicio de esta escena  que el dominio de la función   
es Dom y = (- ∞, -1]U[3 , ∞)

EXERCICI 3.- Calcula en el teu full d'activitats  el DOMINIO de les següents funcions, representant prèviament les funcions que apareixen dins de l’arrel, i comprovant els teus resultats amb la escena anterior:

a)   b)    c)   d)  e)           
 f)

Analíticamente para hallar el DOMINIO de la función , se resuelve la inecuación ax² +bx+c 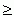 0, de donde se deduce el DOMINIO.

Primero hay que factorizar la función polinómica y=ax²+bx+c

Para ello se resuelve la ecuación ax² +bx+c = 0 y se pueden dar tres casos:

A) La ecuación tiene dos soluciones reales distintas x₁ y x₂ , por tanto se anula en dos puntos, en los cuales la función cambia de signo.
La factorización será: y=ax²+bx+c = a (x-x₁)(x-x₂).
Se divide la recta real en tres intervalos (-∞,x₁); (x₁,x₂); (x₂,∞) suponiendo x₁< x₂
Y se estudia el signo del producto a (x-x₁)(x-x₂) a través del de sus factores:  

Solución de la inecuación ax2 +bx+c  0

(-∞, x1] U [x2, ∞)

DOMINIO de la función

(-∞, x1] U [x2, ∞)

Solución de la inecuación ax2 +bx+c 0

[ x1, x2 ]

DOMINIO de la función

[ x1, x2 ]

B) La ecuación tiene una solución real doble x₁ , por tanto se anula en un sólo punto, y en los demás la función tiene siempre el mismo signo.
La factorización será: y=ax²+bx+c = a (x-x₁)²  
En este caso (x-x₁)²  0 siempre

a>0	a(x-x1)2 0	Solución inecuación  ax2+bx+c0	R todos los nos reales	DOMINIO de la función	D=R
a<0	a(x-x1)20		x = x1		D=x1

 C) La ecuación no tiene solución real, y=ax²+bx+c  no se factoriza, no se anula en ningún punto, y la función siempre tiene el mismo signo.  

Todo esto parece muy complicado, pues al final no son tres casos, sino seis, pues de cada apartado hemos sacado dos.

La mejor forma de tener claro el cálculo del dominio de las funciones es hacer el estudio analítico y a continuación el gráfico, para entender mejor cada caso.
Resuelve detenidamente el ejercicio siguiente y te aseguro ÉXITO

EXERCICI 4.- Donades les funcions: a)     b)     c) 
d)    e)     f) 
Primer.- Agafes la primera i troba en el teu full d'activitats ,el seu DOMINI analíticament segons les instruccions donades en l’apartat 1.2.2 d’aquesta unitat i que es troba en aquesta mateixa pàgina.  
Segon.- Introdueix els valors de a, b i c en la escena de més a dalt i que pertany al apartat 1.2.1 d’aquesta mateixa pàgina, per a veure el seu DOMINI gráficamente.
Tercer.- Torna a fer els apartats anteriors per a les altres funcions.