TRASLACIONES: NIVEL BÁSICO
Geometría
 
1.  TRASLACIÓN DE PUNTOS

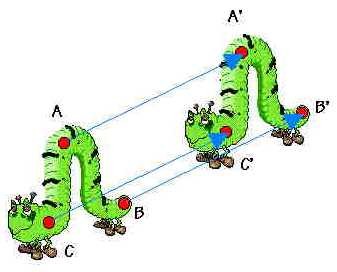traslacion.jpg (11442 bytes)En el dibujo, el gusano de la izquierda se transforma en el gusano de la derecha. Se han señalado algunos puntos en el gusano de la izquierda (A, B, C) y los correspondientes en el gusano de la derecha (A', B', C'), transformado del primer gusano.

Como puedes observar, los vectores que unen cada punto del gusano de la izquierda con sus transformados del gusano de la derecha (AA', BB', CC') tienen el mismo módulo, la misma dirección y el mismo sentido. Además, el gusano de la derecha tiene la misma forma y el mismo tamaño que el gusano de la izquierda. A este movimiento se le llama TRASLACIÓN DE VECTOR v, siendo v el vector libre definido por cualquiera de los vectores anteriores.

Se llama traslación TRASLACIÓN DE VECTOR libre v a una transformación que asocia a cada punto A del plano otro punto A1=T(A) de manera que el vector AA1 sea igual al vector v.

Los elementos que no varían al aplicarles una traslación se denominan invariantes o dobles en esa traslación.

En la escena siguiente está representado el vector v = VW que define una traslación en el plano. Observa las coordenadas del punto A (1,2) y las de su trasladado, A1 (4,4). Comprueba cómo cambian las coordenadas de A1 al desplazar el punto A. (El botón inicio devuelve la figura a su posición inicial).
 

 
 
Actividad para escribir en las HOJAS DE TRABAJO 1.- Encuentra las coordenadas de los puntos transformados, en la traslación definida por el vector v anterior, de los puntos de coordenadas (- 5, - 4), (- 3, - 1), (- 4, - 2). (Utiliza los parámetros x e y para dibujar estos puntos en la posición del punto B). ¿Cuáles serían las coordenadas del transformado del punto B (x, y)?.
   
Actividad para escribir en las HOJAS DE TRABAJO 2.- Si cambiamos la posición de los puntos V y W, obtenemos un nuevo vector v. Sitúa el punto V en las coordenadas (- 6, 1) y el W en (- 2, 3). Calcula de nuevo las coordenadas de los puntos transformados de (- 5, - 4), (- 3, - 1), (- 4, - 2). ¿Cuáles serían ahora las coordenadas del transformado del punto B (x, y)?.
   
Actividad para escribir en las HOJAS DE TRABAJO 3.- Si V (x1, y1) y W (x2, y2),   ¿cuáles serían las coordenadas del transformado del punto B (x, y)?.

 

 

 
2. TRASLACIÓN DE SEGMENTOS
Para trasladar un segmento, debemos calcular los transformados de los extremos del segmento y unirlos.

En esta escena se muestra una traslación de vector v.

 
 
Actividad para escribir en las HOJAS DE TRABAJO 4.- La longitud de los segmentos AB y CD es de 4 unidades, ¿cuál es la longitud de los segmentos transformados A1B1 y C1D1? ¿Son paralelos los segmentos AB y A1B1? ¿Y los segmentos CD y C1D1?. Desplaza los puntos A y B hasta obtener un segmento de longitud 6,5, ¿cuál es ahora la longitud del segmento transformado? ¿Son paralelos los dos segmentos AB y A1B1?.
   

Actividad para experimentar y observar

 5.- Repite las operaciones anteriores para una traslación de vector v (4, 2). (Utiliza los parámetros v1 y v2 para cambiar el vector  v)
   
Actividad para escribir en las HOJAS DE TRABAJO 6.- En el enunciado siguiente, elige la respuesta adecuada.
El transformado de un segmento en una traslación es otro segmento de: a) la misma longitud b) mayor longitud que el inicial c) de longitud menor que el inicial.
   
Actividad para escribir en las HOJAS DE TRABAJO 7.- En el enunciado siguiente, elige la respuesta adecuada. Un segmento y su trasladado son: a) paralelos b) coincidentes c) se cortan.
3. TRASLACIÓN DE RECTAS
Para trasladar una recta es suficiente calcular los transformados de dos puntos de la recta. Al unirlos se obtiene la recta transformada.
 
 
Actividad para experimentar y observar 8.- Comprueba que al desplazar el punto A sobre la recta roja (utiliza el parámetro abscisa), el punto A' transformado del A se desplaza sobre la recta magenta. Comprueba que se sigue manteniendo lo anterior al cambiar la inclinación de la recta roja (el parámetro pendiente permite cambiar la inclinación de la recta roja).
   
Actividad para escribir en las HOJAS DE TRABAJO 9.- ¿Qué ocurre cuando la inclinación da lugar a una recta paralela al vector traslación v? ¿Cuál es, en este caso, el punto A'?.
   
Actividad para escribir en las HOJAS DE TRABAJO 10.- En el enunciado siguiente, elige la respuesta adecuada. La transformada de una recta en una traslación es otra recta:a) paralela b) coincidente c) secante.
   
Actividad para escribir en las HOJAS DE TRABAJO 11.- En el enunciado siguiente, elige la respuesta adecuada. Los elementos dobles en una traslación son: a) las rectas que pasan por el origen b) Los segmentos paralelos al eje de abscisas c) las rectas paralelas al vector traslación.

 

 

 

 
4. TRASLACIÓN DE UNA FIGURA
Si en una figura trasladamos todos sus puntos obtendremos otra figura que es la figura trasladada de la figura inicial.
Actividad para experimentar y observar 12.- El triángulo de vértices ABC se puede trasladar formando un nuevo triángulo A1B1C1. Cambia las coordenadas del vector para comprobar que el triángulo trasladado siempre es el mismo, pero colocado en distintas posiciones.
   
Actividad para escribir en las HOJAS DE TRABAJO 13.- Mueve con el ratón el vector de la traslación que está colocado en la parte superior de la escena y superponlo encima de los vectores que trasladan los vértices. Haz coincidir el origen del vector con cualquier punto del triángulo original ¿Con qué punto coincide el extremo del vector?
   
Actividad para escribir en las HOJAS DE TRABAJO 14.- Dibuja en tu cuaderno un motivo (a ser posible una figura no simétrica) y trasládala varias veces variando el vector. También lo puedes hacer dibujando muchas figuras iguales y después recortando y pegando.
   
Actividad para experimentar y observar 15.- Traslada la figura con un vector horizontal (v2=0), y repite la traslación del nuevo motivo trasladado utilizando el mismo vector, reitera el proceso varias veces. La figura que se obtiene se llama FRISO, y es muy utilizado en la decoración y el diseño.
 
       
           
Joaquín Comas Roqueta
 
© Ministerio de Educación y Ciencia. Año 2007