Si todos los valores de las variables cumplen exactamente una relación exacta, entonces existe una función o fórmula que las relaciona. En este caso se dice que la relación entre las variables es funcional.

Así por ejemplo, la longitud L de una circunferencia y su radio r están perfectamente correlacionados pues se verifica exactamente que :

L  = 2p r

Por el contrario, si se lanzan simultáneamente dos dados unas cuantas veces, no existirá una relación entre los puntos que se obtengan en cada dado (salvo que los dados estén cargados), es decir no existirá correlación entre las puntuaciones de cada dado.

En otros casos, parece que existe cierta correlación o dependencia, aunque ésta no sea perfecta. Por ejemplo, las variables altura y peso de los individuos parecen tener cierto grado de relación aunque no exista una fórmula que nos permita adivinar el peso de un individuo conocida su altura.

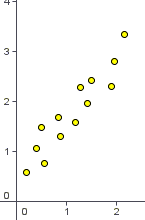
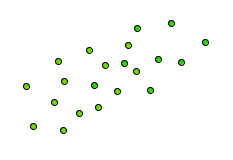
 Sólo con observar el diagrama de dispersión nos podemos hacer una idea de si existe más o menos relación entre ambas variables y del tipo de relación existente. Nos podemos encontrar los siguientes casos:

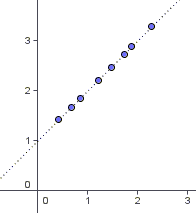
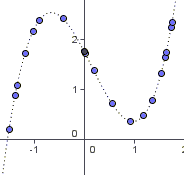
 Dependencia funcional. Cuando todos los puntos del diagrama de dispersión están situados en la gráfica de una función.