ESTADÍSTICA
Tema 2: Distribuciones  Estadísticas  Bidimensionales
4.- CORRELACIÓN   LINEAL.

Vamos a estudiar un coeficiente que nos permita cuantificar la correlación lineal de las dos variables. Antes necesitamos conocer un parámetro conjunto para ambas variables, llamado covarianza.

Se define la covarianza de la siguiente forma:

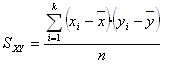
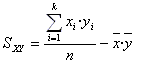
  Haciendo cálculos, esa fórmula es equivalente a :

 
Ahora ya sí estamos en condiciones de definir el siguiente coeficiente.
 

Coeficiente de correlación lineal de Pearson. Se define este coeficiente como el cociente entre la covarianza y el producto de las desviaciones típicas de ambas variables, es decir:

 

 

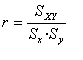
          Este coeficiente tomará siempre valores comprendidos entre -1 y 1. Según los valores que tome, podremos deducir que:
  • Si r=1, existe dependencia funcional, todos los puntos del diagrama de dispersión están situados en una línea recta creciente.
  • Si 0<r<1, la correlación es positiva, y será más fuerte cuanto más próximo a 1 esté.
  • Si r=0, no existe correlación lineal y se dice que las variables están incorreladas, pero puede existir correlación curvilínea.
  • Si -1<r<0, la correlación es negativa, y será más fuerte cuanto más próximo a -1 esté.
  • Si r= -1, existe dependencia funcional, todos los puntos del diagrama de dispersión están situados en una línea recta decreciente.

¡OJO!, no hay que confundir independiente con incorreladas. Si dos variables son independientes, no hay ninguna relación entre ellas, y por tanto en particular, tampoco la habrá lineal, es decir, son incorreladas. Pero puede pasar que siendo incorreladas no sean independientes, pues pueden tener relación las variables aunque no sea lineal.

En la siguiente escena puedes comprender mejor el significado del coeficiente de correlación lineal. Aparecen doce puntos que puedes mover libremente por toda la escena con el ratón. En cada movimiento que hagas te aparecerá el valor del coeficiente de correlación  lineal de Pearson.   

    

Otro coeficiente importante es el llamado Coeficiente de Determinación, que se representa por R2 y se define como el coeficiente de correlación al  cuadrado; esto es R2 = r2.
Este coeficiente es importante pues pasado a porcentaje ( es decir multiplicado por 100 ), nos da el tanto por ciento de dependencia lineal entre las variables.

Por ejemplo si r=0,8432, R2 = 0.711, lo que significa que la dependencia entre las variables es del 71.1 %

 

ACTIVIDADES

 

Actividad 1.

     a) Coloca los puntos en una línea recta creciente ¿Cuánto vale el coeficiente de correlación lineal?

     b) ¿Puede ser el coeficiente mayor que 1?

     c) Separa poco a poco los puntos de la línea recta y observa como disminuye el coeficiente.

Actividad 2.

     a) Coloca los puntos en una línea recta decreciente ¿Cuánto vale el coeficiente de correlación lineal?

     b) ¿Puede ser el coeficiente menor que -1?

     c) Separa poco a poco los puntos de la recta y observa como se aleja de -1 el valor de r.

Actividad 3.

      Intenta distribuir los puntos de forma que el coeficiente de correlación lineal valga 0. Explica qué tiene que pasar para que dicho coeficiente valga 0.

Actividad 4.

      a) Coloca los puntos intentando construir una parábola. ¿Cuánto vale el coeficiente de correlación lineal? ¿Hay correlación lineal?¿Hay correlación curvilínea? ¿Fuerte o débil? Explica esta situación.

     b) Coloca ahora los puntos en dos líneas perpendiculares que se cruzan (por ejemplo paralelas a las bisectrices de los cuadrantes y que tenga seis puntos cada línea) ¿Cuánto vale el coeficiente de correlación lineal? ¿Es lógico este resultado? ¿Por qué?

     c) Construye otros diagramas de dispersión que se te ocurran y analiza el valor de r.

 

Indice Actividades.