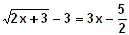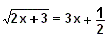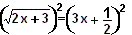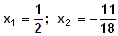ECUACIONES REDUCIBLES A CUADRÁTICAS

1. Las ecuaciones que, directamente o mediante transformaciones de equivalencia, se pueden expresar de la forma: ax²ⁿ+bxⁿ+c=0, con a0; mediante el cambio de variable z=xⁿ se pueden expresar como una ecuación de segundo grado así: az²+bz+c=0

Una vez resuelta esta ecuación, las soluciones de la ecuación original se determinan resolviendo x=.
Entre estas ecuaciones se hallan las bicuadradas, ecuaciones de cuarto grado en las que no aparecen términos de tercero ni de primer grado.

Ejemplos: x⁴ - 5x² +4 = 0 ;  x⁴ - 4 = x² - 1

Para resolver este tipo de ecuaciones se procede inicialmente igual que para las de segundo grado, es decir, operar hasta que no haya denominadores y expresar la ecuación con el segundo miembro igualado a 0.

Gráficamente se pueden resolver como en el caso de las de segundo grado, representando la gráfica correspondiente al primer miembro de la ecuación una vez igualado a 0

2. Ecuaciones con radicales, son aquellas en la que la incógnita aparece en el radicando de una raíz

Para su resolución se hace necesario elevar a una determinada potencia que elimine algún radical. Esto se consigue aislando en uno de los miembros de la ecuación a uno de los radicales.

Esta transformación dará lugar a una nueva ecuación no necesariamente equivalente; es decir, a una nueva ecuación que tiene todas las soluciones de la primera, pero que puede tener alguna más, por lo tanto, será necesario comprobar, en la ecuación original, todas las soluciones obtenidas.

 

Ejemplos:

A) Ejemplo, resuelve x⁴ - 5x² + 4 = 0

1. realizamos un cambio de variable, x² = z, y reescribimos la ecuación: z² - 5z + 4 = 0
2. resolvemos esta escuación, z₁ = 1 y z₂ = 4
3. las soluciones de la ecuación inicial son:

B) Ejemplo, resuelve

1. aislamos la raíz,
2. elevamos al cuadrado,
3. desarrollamos y resolvemos, 36x²+4x-11=0, cuyas soluciones son
4. hacemos la comprobación en la ecuación inicial y sólo la primera de las raíces es solución de la ecuación original, la segunda no.

Escena 1
Vamos a ver representada en la siguiente escena la primera ecuación del ejemplo:
x⁴ - 5x² + 4 = 0
Ahora llamaremos a, b y c respectivamente a los coeficientes de x⁴, x² y término independiente

Puede observarse en la escena que ahora la gráfica ya no es una parábola y que ¡corta al eje X en cuatro puntos!

Naturalmente eso significa que la ecuación tiene cuatro soluciones:

x = - 2 , x = - 1 , x = 1 , x = 2

Busca las soluciones arrastrando el punto rojo o modificando los valores de x en la ventana inferior).

Escena 2

Vamos a representar la ecuación  . Para ello, podemos resolver la ecuación gráficamente expresándola igualada a 0 y representando la ecuación:

Obsérvalo en la escena.

Nos puede sorprender la gráfica, pero pensemos que cuando x es menor que -2, se obtiene la raíz cuadrada de un número negativo, sin valor, luego no puede representarse la curva.

1.-Observa que la curva corta al eje X en el valor x = 2. Escribe el valor de x en la casilla inferior o cámbialo con las flechas.  Comprueba  que el valor x = 2 es solución de la ecuación.
2.-Recuerda y escribe en tu cuaderno  cómo se resuelven numéricamente este tipo de ecuaciones:

En este caso, basta elevar al cuadrado ambos miembros de la ecuación obteniendo:

ecuación de segundo grado que podemos expresar como x² - x - 2 = 0 de la que se obtienen como soluciones: x = 2 y x = -1. La solución x = 2 ya la habíamos observado antes, pero ¿porqué no habíamos visto la solución x = -1? ¿Es realmente otra solución de la ecuación?.

Ficha 3