INECUACIONES DE 2º GRADO

Una inecuación de segundo grado con una incógnita es cualquier desigualdad que, directamente o mediante transformaciones de equivalencia, se pueden expresar de una de las formas siguientes:

ax2+bx+c>0;   ax2+bx+c< 0;    ax2+bx+c0    ó     ax2+bx+c0
con a, b y c reales y a0

 

RESOLUCIÓN:

Resolver la inecuación es encontrar el intervalo o intervalos de la recta real donde se verifica la desigualdad. Para su estudio, vamos a distinguir tres casos según sea el discriminante:
  1. DISCRIMINANTE POSITO,  >0: cuando  b2- 4ac > 0 la ecuacion ax2+bx+c=0 tiene dos soluciones reales distintas, x1 y x2 y podemos escribir:
ax2+bx+c=a·(x-x1)·(x-x2)
Bastará con estudiar el signo de los tres factores para saber el signo del trinomio.
  1. DISCRIMINANTE CERO, =0: cuando  b2- 4ac = 0 la ecuacion ax2+bx+c=0 tiene una solución real doble, x1 y x2 y podemos escribir:
ax2+bx+c=a·(x-x1)2
Como (x-x1)20, el trinomio tendrá el signo del coeficiente a y será nulo para x = x1.
  1. DISCRIMINANTE NEGATIVO, <0: cuando  b2- 4ac < 0 la ecuacion ax2+bx+c=0 no tiene solución real(no hay puntos de corte con el eje X). El signo del trinomio es el mismo que el del coeficiente a.
Gráficamente se comprueba que la solución se obtiene cuando la gráfica correspondiente al primer miembro (parábola) está por encima(por debajo o tangente)  del eje X (y = 0).
Veamos ahora, en la siguiente escena, el estudio de la resolución de una inecuación de segundo grado con una incógnita.
Para realizarlo, expresamos la inecuación dada mediante otra equivalente de la forma ax2+bx+c<0 (el signo de la desigualdad será el que se nos dé en la inecuación que nos propongan):

Escena 1

La inecuación que se propone es: -5x2+3x+8<0
es decir, buscamos los valores de x que le dan al trinomio un valor negativo.

Está enmarcada en el primer tipo, >0,
Tiene dos raíces reales y distintas:
x1=-1; x2= .
Por lo tanto, se puede factorizar:

En la escena se desarrolla el estudio del signo, de cada factor variable, a lo largo de toda la recta real.
Con el signo del trinomio encontramos el intervalo(o intervalos) solución

Cambia el signo de relación para ver como varía la solución.

Resuelve en la escena las inecuacones:
a) x(x-4) < 2x2; b) x2 - 2x + 8 0; c) - x2 + 6x - 9 0
Para cada una de las inecuaciones anteriores, cambia en la escena los valores de a, b y c y el signo de relación.

Escena 1

Veamos, en la escena, la resolución gráfica de una inecuación de segundo grado con una incógnita.
Para hacer el estudio gráfico, expresamos la inecuación de la forma ax2+bx+c>0; transformando, si es necesario, la inecuación inicial.
(el signo de la desigualdad será el que se nos dé en las inecuaciones que nos propongan). En la escena adjunta tenemos resuelta la inecuación: -5x2+3x+8 < 0
Moviendo el punto P por la recta real, puedes comprobar el valor del trinomio y, por tanto, la verificación de la inecuación en el intervalo solución.

Resuelve en la escena las siguientes inecuaciones (escribe con los controles inferiores, a, b y c, los coeficiente y con el control superior, relación, el signo de relación correspondientes).

a)   x2 - 3x + 2 0
b)   1 - 2x < x - x2 + 1

Cuando el signo de la desigualdad incluya el = (como el caso a) ), el intervalo o intervalos solución deben ser "cerrados" ya que los extremos (cuando no son infinito) cumplirán la inecuación. Pueden ser, por ejemplo:

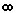 [0 , 2], [3, [,  etc.

Ficha 4

[anterior ] [inicio]