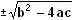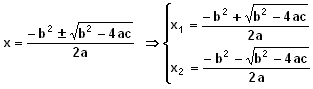ECUACIONES DE 2º GRADO

Ecuaciones de segundo grado, son  aquellas en las que la incógnita aparece al menos una vez elevada al cuadrado (x2).
Por ejemplo: 3x2 - 3x = x - 1.
Si realizamos transformaciones de equivalencia de forma que en el segundo miembro quede 0, otenemos: 3x2 - 4x + 1 = 0, que es la forma en que vamos a expresar todas la ecuaciones de segundo grado para resolverlas.

En muchos casos, una vez conseguida esta forma, la ecuación se puede simplificar, por ejemplo:

Ejercicio: Expresa en la forma más simple y simplificada posible, la ecuación:

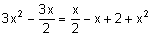Primero buscaremos un denominador común para eliminar los denominadores existentes. Llegaremos a:
6x2 - 3x = x - 2x + 4 + 2x2
y expresaremos todos los términos en el primer miembro: 4x2 - 2x - 4 = 0, simplificando (dividiendo todo por 2) nos queda:
2x2 - x - 2 = 0.
Por lo tanto, llamamos ecuación de segundo grado a toda ecuación que, directamente o mediante transformaciones de equivalencia, se puede expresar de la forma:
ax2 +bx + c = 0  donde  a0

Al ser de grado dos, siempre tiene dos soluciones.

La interpretación geométrica de la ecuación de segundo grado se obtiene a partir de la gráfica de la función y=ax2+bx+c, que es una parábola; donde la solución de la ecuación ax2+bx+c=0 son los puntos de dicha gráfica cuando y=0, es decir, los puntos de corte de la parábola con el eje de abscisas, OX,


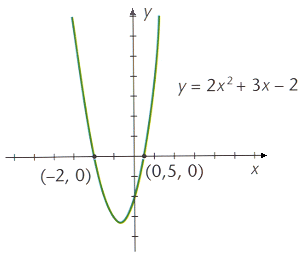
es decir, las soluciones de la ecuación 2x2+3x-2=0 son x1=-2 y x2=0,5

 

RESOLUCIÓN DE LA ECUACIÓN DE SEGUNDO GRADO

La solución analítica de una ecuación de segundo grado se obtiene al considerar que el término de grado dos es un cuadrado perfecto y forma parte del desarrollo del cuadrado de un binomio, para ello haremos las siguientes transformaciones de equivalencia:
    1. multiplicamos por 4a los dos miembros de la ecuación, 4a2x2+4abx+4ac=0
    2. sumamos b2 en ambos miembros, 4a2x2+4abx+4ac+b2=b2, o bien así, (2ax)2+2·2ax·b+b2+4ac=b2
    3. lo expresamos como el cuadrado de un binomio, (2ax+b)2+4ac=b2
    4. eliminamos 4ac del primer miembro y extraemos la raíz cuadrada, 2ax+b=
    5. despejando x nos queda, 

Ejemplo, resuelve 3x2-3x-18=0
    1. multiplicamos por 12(4a), 36x2-36x-216=0
    2. sumamos 9(b2), 36x2-36x+9- 216=9; o bien, (6x)2-2·6x·3+32-216=9
    3. lo expresamos como el cuadrado del binomio, (6x-3)2=225
    4. extraemos la raíz cuadrada, 6x-3=±15
    5. despejamos x, obtenemos x1=3 y x2=-2
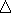Al radicando, b2- 4ac, se le da el nombre de discriminante de la ecuación y se representa por la letra griega delta mayúscula: . Analizando el valor del discriminante, podemos hacer la siguiente discusión:
  • si >0, la raíz es un número real y se obtienen, por tanto, dos raíces reales distintas, x1x2
  • si =0, la raíz es cero, luego, obtenemos dos raíces iguales, es decir, diremos que la raíz es doble,x1=x2
  • si <0, la raíz es un número imaginario o complejo(no real), por lo tanto, se obtienen dos raíces imaginarias.

Asigna a las letras (coeficientes) "a", "b" y "c" los valores correspondientes para cada ecuación (puedes hacerlo con las "flechas" de las ventanas o borrando los valores actuales y escribiendo los nuevos directamente).
(Modifica, si lo deseas, el valor de la "escala" si no se ve la gráfica completa)
Mueve el punto rojo hasta encontrar el punto de corte de la parábola con el eje X. Puedes ver los valores de x en la ventana inferior..

Ficha 1

[anterior ][inicio] [siguiente]