DOS ECUACIONES LINEALES...
¿PUEDEN TENER ALGO EN COMÚN?

Álgebra

 

1.  LA REUNIÓN.

Centrándonos en nuestra historia, y retomando lo último que vimos, llegamos a probar que las soluciones de una ecuación lineal sólo se pueden colocar en línea recta. Ahora bien, qué es lo que pasa cuando dos ecuaciones se reunen para ver si tienen alguna pertenencia (solucion) en común.

Bien, pues volviendo a nuestro cuento, la Sra. Ecuación Lineal quedó un día para ver a una amiga que trabajaba en una oficina cercana a su casa.

Al llegar al punto de encuentro, ambas se encerraron bajo llave y se pusieron a charlar tranquilamente. Claro está, tal y como pasa en la vida real, dos personas pueden tener en común algo, muchas cosas o nada. Pues en el caso de las ecuaciones lineales pasaba algo parecido. Sólo que en su caso, o bien tenían en común una solución, o bien infinitas, o bien ninguna.

Para verlo con más detalle y para que todo no quede en el aire con simples palabras, vamos a realizar unos sencillos ejercicios donde podreis comprobar que todo esto es cierto.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.


1.- En la escena,  que se muestra junto a este enunciado, tienes un sistema de ecuaciones lineales con dos incógnitas. Para cada ecuación lineal, contruye en tu cuaderno de trabajo dos tablas de soluciones arbitrarias, una para cada ecuación lineal.

2.- Ahora, en tu cuaderno de trabajo, construye dos tablas de valores, una para cada ecuación lineal, para valores enteros de "x" desde -3 hasta 3. ¿Qué tienen en común ambas tablas?.

3.- ¿Sería capaz de representar gráficamente las soluciones de ambas ecuaciones?. Recuerda, tanto en un caso como en otro, sus soluciones están en sobre una recta, luego si tienes dos puntos, tienes la recta que pasa por esos puntos y así todas las soluciones de esa ecuación. Inténtalo, esboza en tu cuaderno de trabajo las soluciones de ambas ecuaciones sobre un sistema de coordenadas. ¿Dónde crees que estará la solución del sistema?. Responde a esta última pregunta en tu cuaderno de trabajo.

(Recuerda que localizando dos soluciones en el sistema cartesiano, tendrás los dos puntos sobre los que pasa la recta de soluciones)

 
Hemos visto con el ejercicio anterior que, mediante el uso de tablas es posible encontrar una solución a un sistema de ecuaciones lineales. Ahora bien, ¿Qué ocurriría si la solución común no se encuentra en x=1 como antes?. Supongamos que la solución común se encuntra en x=3,15. Realmente sería muy complicado, mediante tablas, hallar la solución del sistema. Y, por otro lado, ¿Qué ocurriría si las ecuaciones no tienen una solución común?. 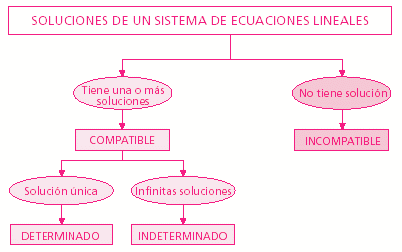Podríamos estar la vida entera haciendo cálculos con las tablas sin poder encontrar solución alguna a nuestro sistema.

Ello nos lleva a dos conclusiones fundamentales:

1ª) El sistema de solución mediante tablas no es efectivo, al menos, no en todos los casos.

2ª) El hecho de que existan sistemas con única solución, infinitas soluciones o ninguna solución lleva a la necesidad de distinguirlos o clasificarlos de alguna manera.

2. LAS REUNIONES SE VUELVEN MÁS COMPLEJAS

En el ejercicio anterior, hemos podido comprobar que existe una solución común a ambas ecuaciones.  Pero, tal y como hemos comentado antes, no todos los sistemas se resuelven mediante tablas. Y no porque no se pueda, sino porque sería más o menos costoso según el tipo de sistema. Y eso, a priori, no lo sabremos.


Recordando la historia de nuestra Sra. Ecuación Lineal  al día siguiente de haberse reunido con su amiga, fué a ver a su hermana, una hermana que era gemela, con lo cual, compartían  muchas cosas. Así, cuando se encerraron bajo llave y pusieron sus soluciones sobre la mesa, vieron que tenían las mismas. Ambas se quedaron estupefactas cuando vieron el conjunto de soluciones que habían formado. Y, claro, al poco tiempo cayeron en la cuenta de que, al ser gemelas, era una imagen y semejanza de la otra.

Esta unidad interactiva requiere la máquina virtual de Java J2RE.


4.- En la siguiente escena tienes un sistema de ecuaciones lineales y la gráfica correspondiente a las soluciones de la primera ecuación. De ese sistema, modifica la segunda ecuación lineal hasta  obtener la misma que la primera y observa que ha ocurrido con sus gráficas, verás que tienen las mismas soluciones, pues ambas gráficas coinciden. De este modo, el sistema tiene infinitas soluciones.


5.- Modifica de nuevo la segunda ecuación y obtén otra ecuación distinta de manera que sus graficas de soluciones vuelvan a coincidir. Ahora, fíjate bien en la  primera ecuación del sistema y la que obtuviste. ¿Qué relación  crees que tienen entre sí ambas ecuaciones?.

6.- Del mismo modo que modificaste la segunda ecuación en los ejercicios 4 y 5, obtén otra ecuación de manera que su gráfica de soluciones sea paralela a la de la primera ecuación. ¿Cuántas soluciones en común tiene?. ¿Cuántas soluciones crees que tendrá entonces el sistema?. Anota estas preguntas y tus respuestas a las mismas en tu cuaderno de trabajo.

7.- Por último, utilizando la escena adjunta, configura una ecuación lineal que no siga el patrón de las ecuaciones halladas en los ejercicios 4, 5 y 6. ¿Cuántas soluciones crees que tendrá dicho sistema?. Anota en tu cuaderno de trabajo, la pregunta de este ejercicio, el sistema hallado y la respuesta dada.

Con los ejercicios 4 y 5 hemos podido observar en qué casos un sistema de ecuaciones lineales tiene infinitas soluciones, y esto se da en dos situaciones distintas:


1)  Al ser ambas ecuaciones iguales.

2) Cuando, en el sistema, ambas ecuaciones son equivalentes. Es decir, por ejemplo, la segunda ecuación se obtiene multiplicando ambos miembros de la igualdad, de la primera ecuación, por un número.

A estos sistemas con infinitas soluciones se les denomina compatibles indeterminados.

En cambio, con el ejercicio 6 hemos hallado un sistema que no tiene solución y, en el ejercicio 7, otro con solución única. Con lo cual hemos hallado un sistema incompatible y otro compatible determinado, respectivamente.

Por tanto, los sistemas de ecuaciones lineales se pueden clasificar del siguiente modo.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Germán Domínguez Chorat

 

Ministerio de Educación, Cultura y Deporte. Año 2011

 

 

 

 


Licencia de Creative Commons
Los contenidos de esta unidad didáctica están bajo una licencia de Creative Commons si no se indica lo contrario.