

Para estudiar dos
funciones lineales
a la vez, representamos
sobre los mismos ejes las dos rectas. Las coordenadas del punto de
corte se
hallan resolviendo el sistema formado por las dos ecuaciones . Este
punto tiene
gran importancia en
Vamos a estudiar en concreto el problema dado con el siguiente enunciado
Empezamos a resolver el problema:
Depósito A
Por los datos del problema sabemos que (0,15) es un punto de la función y que la pendiente es m = -2
Con esto podemos escribir la ecuación punto-pendiente y = 15-2x
Depósito B
Como el depósito B al principio está vacio el punto (0,0) pertenece a la función que buscamos y la pendiente m = 1
De esta forma la ecuación de proporcionalidad que lo representa es y = x
En la primera escena representamos la ecuación obtenida para el depósito A:
.
En la segunda representamos la ecuación obtenida para el depósito B:
En la última escena
hacemos la
representación conjunta de
las dos y contestamos las dos preguntas planteadas en el enunciado. Es
decir,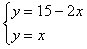
Por tanto los dos depósitos tendrán la misma cantidad de agua cuando pasen 5 minutos desde que se empieza a vaciar el depósito A y a llenar el B y en se momento tendrán 5 litros de agua.
1.- Inventa el enunciado de un problema en el que intervengan
dos funciones lineales (por ejemplo dos empresa A y B cuyos beneficios
vienen dados por y= f(x) , y= g(x) respectivamente. Escríbelo en
tu cuaderno de trabajo. Introduce, por ejemplo, en la última escena los
coeficientes de las funciones y busca la solución a la preguntas que
plantees en dicho enunciado.
Autora: Mª Pilar Arilla Viartola