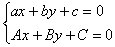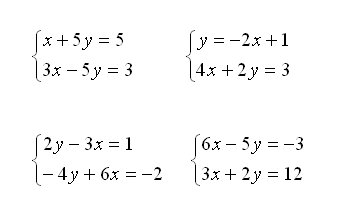Sistemas
de
ecuaciones lineales: Resolución gráfica
1)
Representación de la función lineal y = mx+n
La ecuación y = mx+n se representa por una recta, de forma
que la pendiente de la recta es m (representa la variación de y por
cada unidad
de x) y su ordenada en el origen es n, es decir la recta corta al eje
OY en el
punto (0,n)
En la primera escena vamos a representar una función lineal.
Para ello
vamos a necesitar el cuaderno de trabajo y seguiremos estos pasos:
-
Despejaremos y en la expresión que nos den, es decir, escribiremos la
expresión analítica de la función en la forma y= m x+n siendo m la pendiente de
la recta y n la
ordenada en el
origen.
-
A continuación hacemos una tabla de valores eligiendo para la x
(abcisa) al menos tres valores.
-
Una vez que tengamos tres puntos pertenecientes a la recta,
introducimos en la escena los valores correspondientes a dos de ellos.
Lo haremos utilizando
-
( x1 , y1) para el primer punto y (x2,
y2) para el segundo.
-
Cuando ya tengamos esos valores introducidos la recta quedará
representada y además se indicará en la escena el valor de la pendiente.

1.-
Representa las siguientes funciones lineales. (Para
ello en tu cuaderno de trabajo despeja y, si es que no te la dan la
función en forma explícita) y haz la tabla de valores. Cuando los
tengas introdue los dos puntos en la escena.)
y = 2x+1
y-3x = 2
2x+y = 0
4x+2y=6
2) Resolución
gráfica de
un sistema de ecuaciones lineales
Un sistema de ecuaciones
lineales es un sistema del tipo:
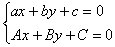
Sabemos
que al resolverlo analíticamente
podemos encontrar:
- Que
el sistema
tenga una única solución.
- Que
el sistema
tenga infinitas soluciones.
- Que
el sistema
no tenga solución.
En el tema de funciones hemos estudiado, que si representamos una
ecuación lineal, su gráfica es una
recta.
También sabemos que si dos rectas tienen la misma pendiente y no
son coincidentes, son paralelas y por tanto no se cortan en ningún
punto, de forma que el sistema no tendrá solución y si son coincidentes
el sistema tendrá infinitas soluciones.
Si tienen distinta pendiente,
se cortan en un punto y en ese caso, dicho punto es la solución del
sistema .
Modifica los valores de a, b, c, A, B, y C
para
comprobar que sucede al variar esos datos.
Nota : ten en cuenta que en la
primera ecuación la pendiente de la recta es m= -a/b y en la segunda
M=-A/B. También pudes utilizar que el vector normal de la primera recta
(a,b) y de la segunda (A,B) son proporcionales si las rectas son
paralelas.
En la escena que aparece a continuación puedes comprobar gráficamente
lo anterior.
1.-
En tu cuaderno de trabajo resuelve analíticamente los siguientes
sistemas lineales y comprueba, en la escena, que la solución obtenida
analíticamente, coincide con la solucíon obtenida gráficamente.
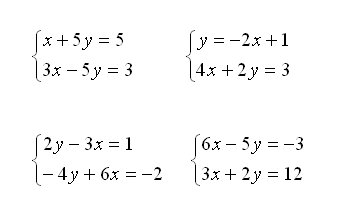



Autora: Mª Pilar Arilla Viartola