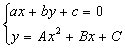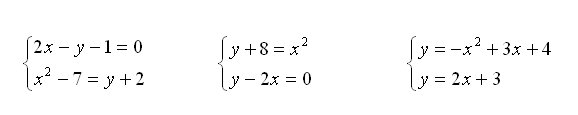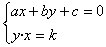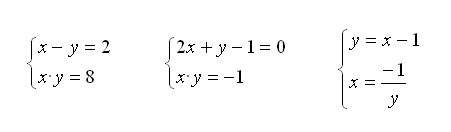Sistemas de
ecuaciones no lineales: Resolución gráfica
En primer
lugar vamos a
ver mediante una escena las posibles soluciones que tiene el sistema no
lineal
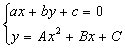
si
lo resolvemos
gráficamente. Para ello representamos la recta y la
parábola.
Sabemos
que al resolverlo analíticamente
podemos encontrar:
- Que
el sistema
tenga una única solución, es decir que la recta sea tangente a la
parábola.
- Que
el sistema
tenga dos soluciones, es decir que la recta corte en dos puntos a la
parábola.
- Que
el sistema
no tenga solución, es decir que la recta y la parábola no tengan ningún
punto en común.
Modifica los valores de a, b, c, A, B, y C
para
comprobar que sucede al variar estos parámetros.
1.
Anota en tu cuaderno de trabajo los valores que les das a estos
parámetros en dos situaciones y apunta en el mismo, la solución que se
mostrará en la escena.
2.En tu
cuaderno resuelve analíticamente los
siguientes sistemas no lineales y comprueba con la escena
que las soluciones obtenidas analíticamente coinciden con las que
obtienes gráficamente (ten
en cuenta que cuando las soluciones no sean números enteros, en la
escena lo que aparece como solución es una aproximación, ya que se está
trabajando con dos decimales)
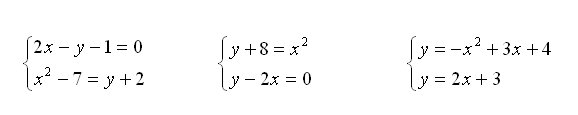
En la siguiente
escena, vamos a ver la resolución gráfica de sistemas de ecuaciones
no lineales del tipo
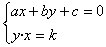
Para ello representamos la recta y la hipérbola.
Sabemos que al resolverlo análiticamente
podemos encontrar:
- Que
el sistema
tenga una única solución, es decir que la recta sea tangente a la
hipérbola.
- Que
el sistema
tenga dos soluciones, es decir que la recta corte en dos puntos a la
hipérbola.
- Que
el sistema
no tenga solución, es decir que la recta y la hipérbola no tengan
ningún
punto en común.
Modifica
los valores de a, b, c, A, B, y C
para
comprobar que sucede al variar estos parámetros.
3.
Anota en tu cuaderno de trabajo los valores que les das a estos
parámetros en dos situaciones y apunta en el mismo, la solución que se
mostrará en la escena.
4.En tu
cuaderno resuelve analíticamente los
siguientes sistemas no lineales y comprueba con la escena
que las soluciones obtenidas analíticamente coinciden con las que
obtienes gráficamente (ten
en cuenta que cuando las soluciones no sean números enteros, en la
escena lo que aparece como solución es una aproximación, ya que se está
trabajando con dos decimales)
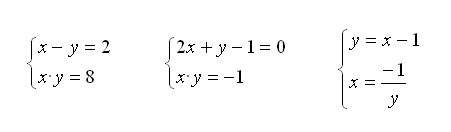


Autora: Mª Pilar Arilla Viartola